• 重温数据结构——图的遍历

    重温数据结构——图的遍历

          首先，我很想说的是，最近这两天寝室里的蚊子，有点多，有点犀利~每天早上起来都要被叮上几个包，有点苦逼。

           另外今天还玩了几把dota2，感觉画面质量是很不错的，但是，手感和dota不一样，而且我的笔记本配置很一般~

           接下来讲今天看的数据结构——图~

           我上个学期在上海泰瑞达的春季招聘中曾被考过这类问题。前面有一题是多态和另外一个名词的解释，有点记不清了。然后还有一道题考的是括号解析，这个很简单的，用栈就能直接处理。然后后面就是连续的两个图的问题。之前好像只是简单的看了看源代码，对于什么是深度优先遍历和广度优先遍历稍微有点认识吧。结果自然是可想而知，比较惨的。当时我在卷子上是这么写的：“今天不会，明天就会了”。当天回去就开始看图论，但是确实是搞的差不多了，不过现在嘛，呵呵~

           首先，图的存储结构有简单的两种：1 邻接矩阵法 2临界表法

           邻接矩阵我觉得是非常明了的一种图的表示方法，当然了，其缺点就是，在图的点数多而连接线少的时候，比较浪费资源。

           我的邻接矩阵简单代码如下：

     1 int main()
 2 {
 3     cout << "Hello world!" << endl;
 4     int Block[5][5] = 
 5     {
 6         0, 1, 1, 1, 0, 
 7         1, 0, 1, 1, 0, 
 8         1, 1, 0, 0, 1, 
 9         1, 1, 0, 0, 1, 
10         0, 0, 1, 1, 0  
11     };
12     Graph tmpGph(Block);
13     tmpGph.DeepSearch();
14     tmpGph.ResetVisit();
15     cout << endl;
16     tmpGph.BFS();
17     //New Job!!!
18 //    GraphList tmpGphLst;
19 //    int nLineNumbers = 0;
20 //    int nItem, Point;
21 //    cout << "How Many Lines Inside?" << endl;
22 //    cin >> nLineNumbers;
23 //    while(nLineNumbers --)
24 //    {
25 //        cout << "Input Line Point A, B" << endl;
26 //        cin >> nItem >> Point;
27 //        tmpGphLst.AddToListByOrder(nItem, Point);
28 //    }
29 //    tmpGphLst.BFS();
30 //    cout << endl;
31     return 0;
32 }

           因为遍历的是无向图，所以我做的是一个对称邻接矩阵，其对应的图是这样的：（其中的箭头你就当他不存在吧，无向图哦）

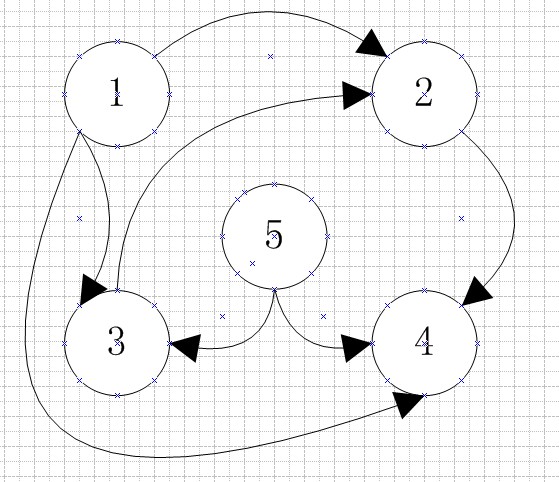
    　　我发现我在写博文题同时，还能提高我的visio绘图能力~不过现在实在不怎么样。一点点练吧。

    　　这样从1点开始进行深度优先遍历，我们很容易就能得出其遍历结果：

    　　1 2 3 5 4

    　　这个结果相信不用我多说吧，具体可以看代码及其运行结果：

    1 int Graph::DeepSearch(int Point)
     2 {
     3     p_nVisitList[Point] = 1;
     4     cout << Point << ends;
     5 
     6     for(int i = 0;i < 5;++ i)
     7     {
     8         if(1 == pBlock[Point][i] && 0 == p_nVisitList[i])
     9         {
    10             DeepSearch(i);
    11         }
    12     }
    13 }

    就是这样一段简单的代码~其中在函数生命中Point的参数默认为0，其运行结果如下： 

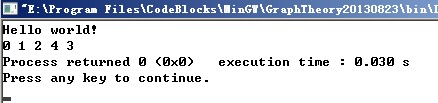
    其中逐个加1，就对应上了1 2 3 5 4了。

    就这么简单。深度优先遍历使用的方法是针对当前的这个点的邻接点进行查找，只要找到了一个未访问的节点，就对这个节点采用同样的方式进行遍历。所以深度优先遍历使用递归是很好的方式，我的那个代码只有13行~

    而邻接矩阵的广度优先遍历则是逐层访问，比较适合邻接表来做。邻接矩阵的广度优先遍历方法如下：

     1 void Graph::BFS()
 2 {
 3     p_nVisitList[4] = 1;
 4     cout << 4 << ends;
 5     queue<int> DL;
 6     DL.push(4);
 7     while(!DL.empty())
 8     {
 9         int val = DL.front();
10         DL.pop();
11         for(int i = 0;i < 5;++ i)
12         {
13             if(1 == pBlock[val][i] && p_nVisitList[i] == 0)
14             {
15                 cout << i << ends;
16                 p_nVisitList[i] = 1;
17                 DL.push(i);
18             }
19         }
20     }
21 }

    运行结果：

          

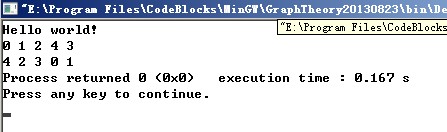
           还是一样的图，运行结果就是第二行的结果。你可以自己算一下对不对（BFS遍历的起始点为4，注意下）。

           邻接表的广度优先遍历

           我觉得，因为邻接表的较为特殊的存储形式，使得其较为适合以广度优先的方式进行遍历。但是需要注意的是，邻接矩阵和邻接表这两种图的存储形式，都能够使用深度优先遍历和广度优先遍历的。

           广度优先遍历的思想是逐层访问，每当当前节点的全部相邻节点都被访问完成之后，再访问下一层节点。

           我在用邻接表表示的图的类中，专门制作了一个方法用于添加点和点关系的函数。通过这个函数，来实现图的创建。

           看下这个类的代码：

     1 class ListNode
 2 {
 3     public:
 4         int val;
 5         int weight;
 6         ListNode * next;
 7     public:
 8         ListNode();
 9 };
10 ListNode::ListNode():val(0), weight(0), next(NULL)
11 {
12     ;
13 }
14 class GraphList
15 {
16     public:
17         GraphList();
18         ~GraphList();
19         void AddToListByOrder(int nitem, int Point);
20         void BFS(int n = 0);//这个广度优先遍历的代码太好写了
21     private:
22         int visit[5];
23         ListNode * Next[5];
24 };

    上面的代码中包含了两个类，一个是邻接表的节点类，另外一个是邻接表本身。代码还是很简单的，而且因为邻接表的特性，使得分层遍历十分方便，看主函数代码结构：

    

    

     1     GraphList tmpGphLst;
 2     int nLineNumbers = 0;
 3     int nItem, Point;
 4     cout << "How Many Lines Inside?" << endl;
 5     cin >> nLineNumbers;
 6     while(nLineNumbers --)
 7     {
 8         cout << "Input Line Point A, B" << endl;
 9         cin >> nItem >> Point;
10         tmpGphLst.AddToListByOrder(nItem, Point);
11     }
12     tmpGphLst.BFS();
13     cout << endl;
    

    

    在看演示效果：
    

     
    

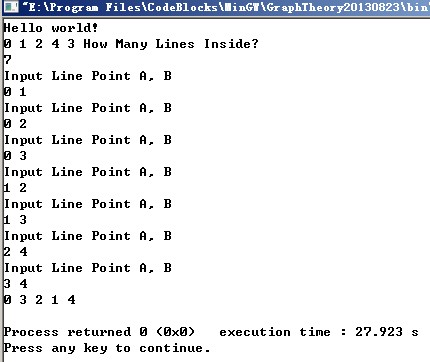
    因为链表采用的是前插法，所以你会看到第二层的遍历结果是3 2 1，反过来的。
    

    很容易发现，在使用邻接表来表示的时候进行广度优先遍历很方便。
    

    图论，我就写这些啦~
    

    最后附上本次的全部代码：
    

    

      1 #include <iostream>
  2 #include <queue>
  3 
  4 using namespace std;
  5 
  6 class Graph
  7 {
  8     private:
  9     //访问控制
 10     int p_nVisitList[5];
 11     int (* pBlock)[5];
 12 
 13     public:
 14     Graph(int (*pParam)[5]);
 15     ~Graph();
 16     //深度优先遍历
 17     int DeepSearch(int Point = 0);
 18     void BFS();
 19     void ResetVisit();
 20 };
 21 
 22 class ListNode
 23 {
 24     public:
 25         int val;
 26         int weight;
 27         ListNode * next;
 28     public:
 29         ListNode();
 30 };
 31 ListNode::ListNode():val(0), weight(0), next(NULL)
 32 {
 33     ;
 34 }
 35 class GraphList
 36 {
 37     public:
 38         GraphList();
 39         ~GraphList();
 40         void AddToListByOrder(int nitem, int Point);
 41         void BFS(int n = 0);//这个广度优先遍历的代码太好写了
 42     private:
 43         int visit[5];
 44         ListNode * Next[5];
 45 };
 46 void GraphList::AddToListByOrder(int nitem, int Point)//前插法，代码好写
 47 {
 48     if(nitem >= 0 && nitem < 5 && Point >= 0 && Point < 5)
 49     {
 50         ListNode * pnewnode = new ListNode;
 51         if(pnewnode == NULL)
 52             return;
 53         pnewnode->val = Point;
 54         pnewnode->next = Next[nitem];
 55         Next[nitem] = pnewnode;
 56     }
 57 }
 58 
 59 void GraphList::BFS(int n)
 60 {
 61     for(int i = 0;i < 5;++ i)
 62     {
 63         if(visit[i] == 0)
 64         {
 65             cout << i << ends;
 66             visit[i] = 1;
 67         }
 68         ListNode * pLNTmp = Next[i];
 69         while(pLNTmp != NULL)
 70         {
 71             if(0 == visit[pLNTmp->val])
 72             {
 73                 cout << pLNTmp->val << ends;
 74                 visit[pLNTmp->val] = 1;
 75             }
 76             pLNTmp = pLNTmp -> next;
 77         }
 78     }
 79 }
 80 
 81 GraphList::GraphList()
 82 {
 83     for(int i = 0;i < 5;++ i)
 84     {
 85         visit[i] = 0;
 86         Next[i] = NULL;
 87     }
 88 }
 89 
 90 GraphList::~GraphList()
 91 {
 92     for(int i = 0;i < 5;++ i)
 93     {
 94         ListNode * ptmpLN;
 95         while(Next[i] != NULL)
 96         {
 97             ptmpLN = Next[i]->next;
 98             delete Next[i];
 99             Next[i] = ptmpLN;
100         }
101     }
102 }
103 
104 void Graph::ResetVisit()
105 {
106     for(int i = 0;i < 5;++ i)
107     {
108         p_nVisitList[i] = 0;
109     }
110 }
111 Graph::Graph(int (*pParam)[5])
112 {
113     for(int i = 0;i < 5;++ i)
114         p_nVisitList[i] = 0;
115     pBlock = pParam;
116 }
117 
118 Graph::~Graph()
119 {
120     ;//nothing!
121 }
122 
123 int Graph::DeepSearch(int Point)
124 {
125     p_nVisitList[Point] = 1;
126     cout << Point << ends;
127 
128     for(int i = 0;i < 5;++ i)
129     {
130         if(1 == pBlock[Point][i] && 0 == p_nVisitList[i])
131         {
132             DeepSearch(i);
133         }
134     }
135     return 0;
136 }
137 
138 void Graph::BFS()
139 {
140     p_nVisitList[4] = 1;
141     cout << 4 << ends;
142     queue<int> DL;
143     DL.push(4);
144     while(!DL.empty())
145     {
146         int val = DL.front();
147         DL.pop();
148         for(int i = 0;i < 5;++ i)
149         {
150             if(1 == pBlock[val][i] && p_nVisitList[i] == 0)
151             {
152                 cout << i << ends;
153                 p_nVisitList[i] = 1;
154                 DL.push(i);
155             }
156         }
157     }
158 }
159 
160 int main()
161 {
162     cout << "Hello world!" << endl;
163     int Block[5][5] = 
164     {
165         0, 1, 1, 1, 0, 
166         1, 0, 1, 1, 0, 
167         1, 1, 0, 0, 1, 
168         1, 1, 0, 0, 1, 
169         0, 0, 1, 1, 0  
170     };
171     Graph tmpGph(Block);
172     tmpGph.DeepSearch();
173     tmpGph.ResetVisit();
174     cout << endl;
175     tmpGph.BFS();
176     //New Job!!!
177     GraphList tmpGphLst;
178     int nLineNumbers = 0;
179     int nItem, Point;
180     cout << "How Many Lines Inside?" << endl;
181     cin >> nLineNumbers;
182     while(nLineNumbers --)
183     {
184         cout << "Input Line Point A, B" << endl;
185         cin >> nItem >> Point;
186         tmpGphLst.AddToListByOrder(nItem, Point);
187     }
188     tmpGphLst.BFS();
189     cout << endl;
190     return 0;
191 }
    

    


    
    
          
    • 

          
  • 

            相关阅读:
    
            
              网络-路由交换-路由基础-华为-OSPF的工作原理
                
    网络-路由交换-路由基础-华为-OSPF报文
                
    常见协议端口号和IP地址
                
    以太网帧类型速查（协议字段）
                
    TCP/UDP端口列表
                
    利用python生成简单的爆破字典
                
    BUU的三道文件包含题
                
    Poc、Exp、Payload、Shellcode的区别
                
    JavaScript Dom操作-增删改节点1
                
    JavaScript 图片轮播
                
                    
          
    • 
          
  • 
            原文地址：https://www.cnblogs.com/matrix-r/p/3279750.html
          
    • 

        

      



      
      

        

        

      

    

  


  

  
Copyright © 2020-2023 
  润新知