Mashmokh's boss, Bimokh, didn't like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh's team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn't able to solve them. That's why he asked you to help him with these tasks. One of these tasks is the following.
A sequence of l integers b1, b2, ..., bl (1 ≤ b1 ≤ b2 ≤ ... ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally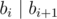 
for all i (1 ≤ i ≤ l - 1).
Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007 (109 + 7).
The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).
Output a single integer — the number of good sequences of length k modulo 1000000007 (109 + 7).
3 2
5
6 4
39
2 1
2
In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].
题意:给你1~n之间的数，让你组成一个长度为k序列，使得后一个的数mod前一个数为0.
思路:后一个数只与前一个数有关，设dp[i][j]表示长度为i的序列中最后一个数字为j，则dp[i][l] = dp[i][l] + dp[i-1][j],其中l%j == 0，l是j的倍数；
1 #include <bits/stdc++.h> 2 #define int long long 3 #define rad rand()%mod+1 4 using namespace std; 5 const int maxn = 1e6+5; 6 const int maxm = 2e3+5; 7 const int mod = 1e9+7; 8 int dp[maxm][maxm]; 9 signed main() 10 { 11 int n, k; 12 while(~scanf("%lld %lld", &n, &k)) 13 { 14 memset(dp, 0, sizeof dp); 15 for(int i=1; i<=n; i++) 16 dp[1][i] = 1; 17 for(int i=1; i<=k; i++) 18 { 19 for(int j=1; j<=n; j++) 20 { 21 for(int l=j; l<=n; l += j) 22 dp[i][l] = (dp[i][l] + dp[i-1][j]) % mod; 23 } 24 } 25 int ans = 0; 26 for(int i=1; i<=n; i++) 27 { 28 ans += dp[k][i]; 29 ans %= mod; 30 } 31 printf("%lld ", ans); 32 } 33 return 0; 34 } 35 /*** 36 37 38 ***/