方法一:R语言
w <- c(75.0, 64.0, 47.4, 66.9, 62.2, 62.2, 58.7, 63.5,
+ 66.6, 64.0, 57.0, 69.0, 56.9, 50.0, 72.0)
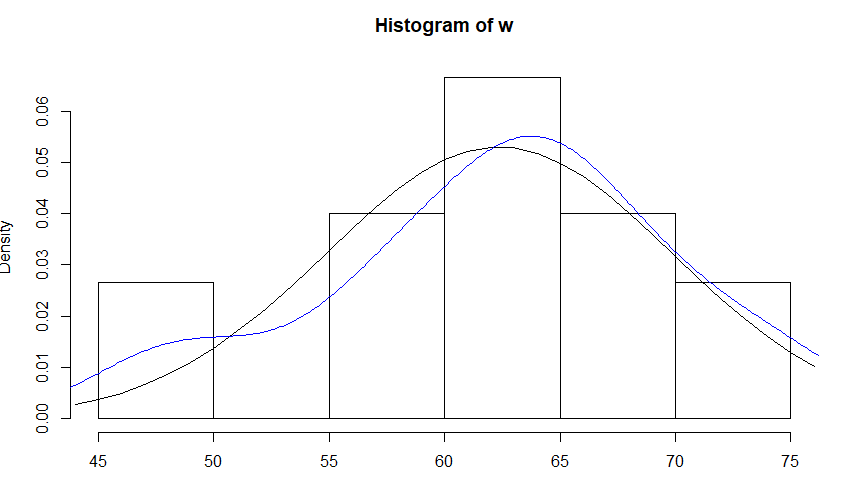
hist(w, freq = FALSE)
lines(density(w), col = "blue")
x <- 44:76
lines(x, dnorm(x, mean(w), sd(w)), col = "black")
lines(density(w), col = "blue")
density是核密度曲线,比正态曲线更拟合
方法二:
参考https://blog.csdn.net/tanzuozhev/article/details/51106291
library(ggplot2)
set.seed(1234)
dat <- data.frame(cond = factor(rep(c("A","B"), each=200)),
rating = c(rnorm(200),rnorm(200, mean=.8)))
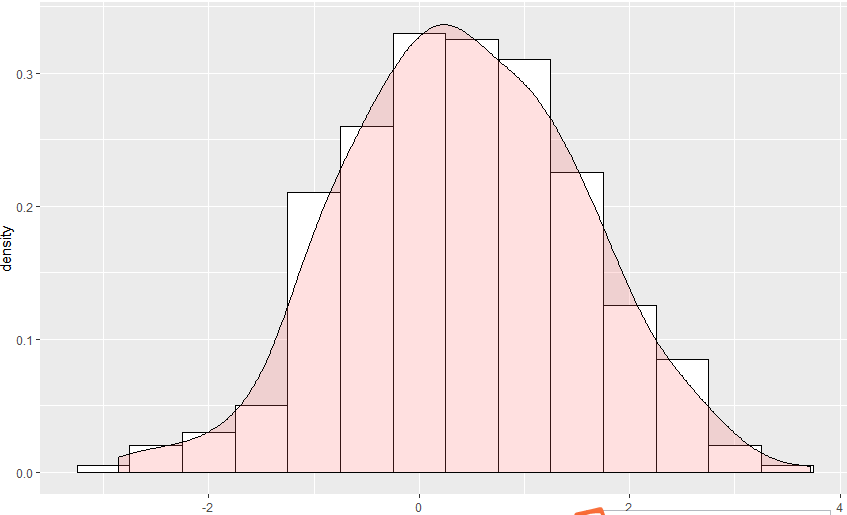
ggplot(dat, aes(x=rating)) +
geom_histogram(aes(y=..density..), # 这一步很重要,使用density代替y轴
binwidth=.5,
colour="black", fill="white") +
geom_density(alpha=.2, fill="#FF6666") # 重叠部分采用透明设置
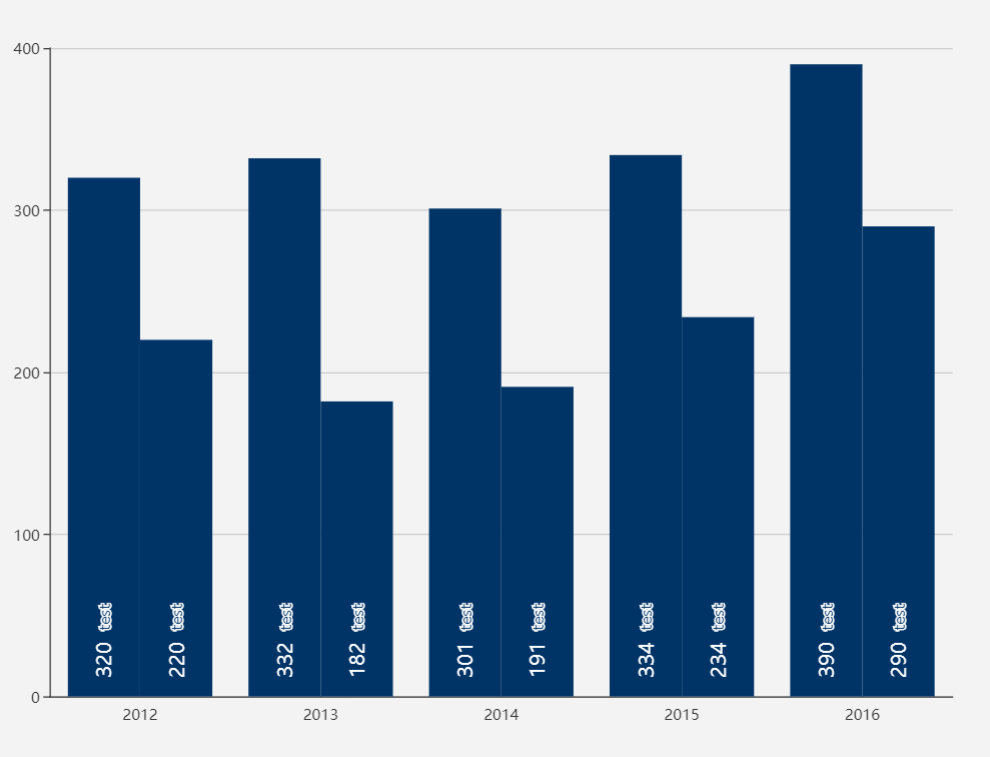
方法三:echarts
https://echarts.baidu.com/examples/editor.html?c=bar-label-rotation
https://github.com/ecomfe/echarts-stat
或者用echarts-stat画直方图或者拟合曲线
方法4:excel
参考https://jingyan.baidu.com/article/f3ad7d0fffa41509c2345b6e.html
注意使用几个函数
=MAX(A:A)
=MIN(A:A)
=ROUNDUP(SQRT(COUNT(A:A)),0) 分组数
极差/分组数=组距
=FREQUENCY(A:A,K18:K34) 求组内计数,先输入一行公式,再选中所有待计数的单元格,F2,ctrl+shift+enter,搞定
=NORMDIST(K18,AVERAGE(A:A),STDEV(A:A),0) 求正态分布的函数密度
插入直方图,选中直方图后,设置数据系列格式
选择组距为0,颜色,边框,
选择数据,可以点击编辑,换别的数据,可以添加新的数据,横坐标的label修改的话,选择“水平(分类)轴标签”
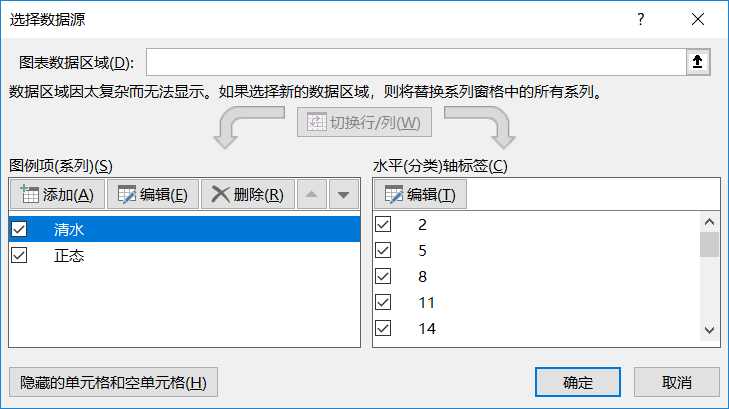
再插一个直方图,选中图形,鼠标右键,
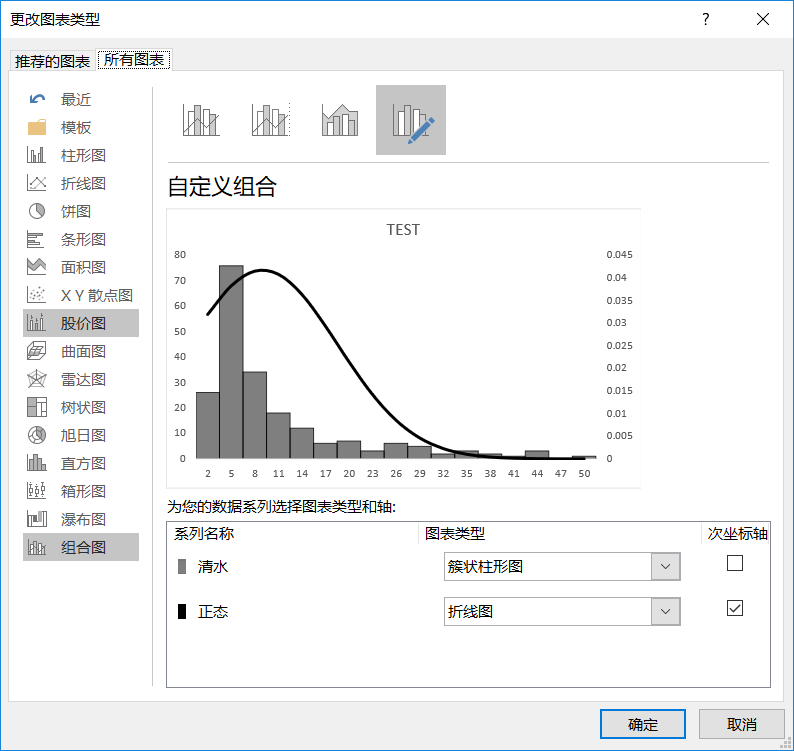
别忘了,选中曲线,设置平滑线。
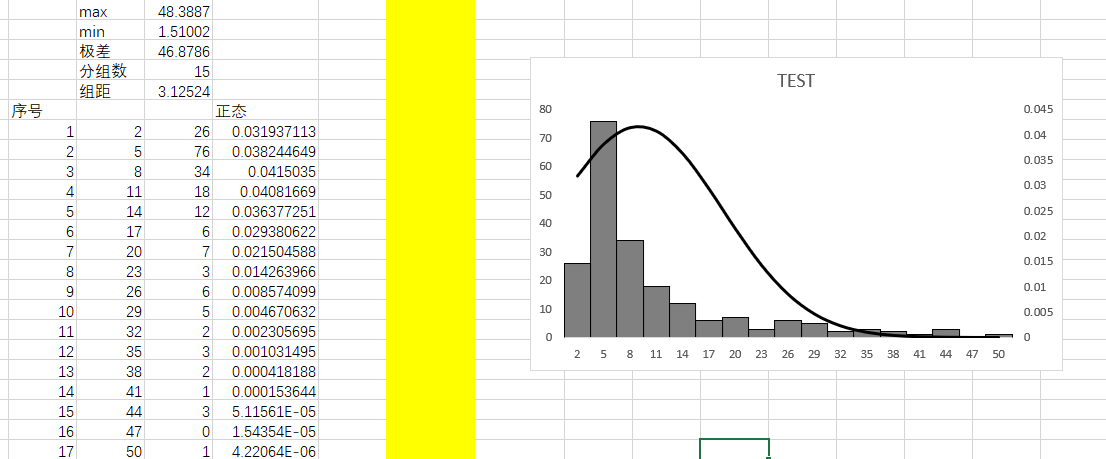
* 附上lines和curve的区别
lines得直接输入x,y值;curve可以直接接受函数为输入值,例如curve(sin)。
lines默认加载现在的图上,curve默认是新图。
*附上lines和abline的区别
函数lines()其作用是在已有图上加线,命令为lines(x,y),其功能相当于plot(x,y,type="1")
函数abline()可以在图上加直线,其使用方法有四种格式。
(1)abline(a,b)
表示画一条y=a+bx的直线
(2)abline(h=y)
表示画出一条过所有点得水平直线
(3)abline(v=x)
表示画出一条过所有点的竖直直线
(4)abline(lm.obj)
表示绘出线性模型得到的线性方程
lines()函数做的是一般连线图,其输入是x,y的点向量。
abline()函数做的是回归线,其输入是回归模型对象。
plot()函数被调用时即创建一副新图,而lines()函数是在已存在的图形上添加信息,并不能自己生成图形。
*附上如何使用R语言做正态性检验,数据是否服从正态分布
两种办法
x<-c(39,55,51,47,32,25,34)
shapiro.test(x)
看p值大不大0.05,越大越正态
用R语言自带的Kolmogorov-Smirnov方法
ks.test(x, "pnorm", mean = mean(x), sd = sqrt(var(x)))
看p值大不大0.05,越大越正态
或者画一个qq图
norm.test<- function(input.data,alpha=0.05,pic=TRUE){
if(pic==TRUE){#画图形
dev.new()
par(mfrow=c(2,1))
qqnorm(input.data,main="qq图")
qqline(input.data)
hist(input.data,frep=F,main="直方图和密度估计曲线")
lines(density(input.data),col="blue") #密度估计曲线
x<- c(round(min(input.data)):round(max(input.data)))
lines(x,dnorm(x,mean(input.data),sd(input.data)),col="red") #正态分布曲线
}
sol<- shapiro.test(input.data)
if(sol$p.value>alpha){
print(paste("success:服从正态分布,p.value=",sol$p.value,">",alpha))
}else{
print(paste("error:不服从正态分布,p.value=",sol$p.value,"<=",alpha))
}
sol
}