三角数字
给定一串数字1,3,6,10,15,21.......是否能推出后面几项的值呢。
显然第N项的值等于第N-1项+N
a[N]=a[N-1]+N该种数列被称为三角形数字。

由此可以根据规律计算第N项的值。可以使用循环的方法来计算第N项的值
int triangle(int n)
{
int total=0;
while(n>0)
{
total=total+n;
--n;
}
return total;
}
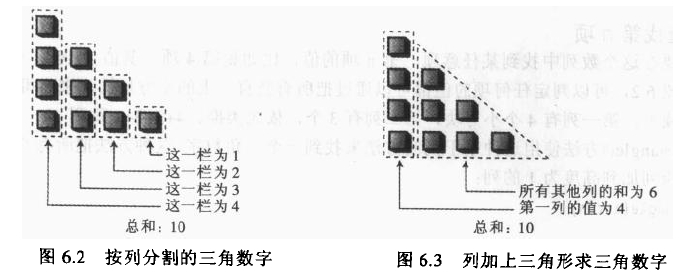
使用循环的方法来算挺好,但是可以考虑用递归,正如两幅图之间对比的那样。
int triangle(int n)
{
return (n+triangle(n-1));
}
但是显然上面的程序永远不会结束,陷入了一个庞氏骗局,因为没有终止的条件。
int triangle(int n)
{
if(n=1)
return 1;
else
return (n+triangle(n-1));
}
为了清楚地观察到递归函数的执行过程,程序中加入了测试语句。可以看到整个递归的调用过程。



通过上面的三幅图看到整个递归程序的执行过程。
阶乘
阶乘实际上就是把上面三角形的问题,稍微改变一下。
递归的二分查找
下面两幅图对比,可以看到我们将递归插入到了二分查找中


图二实质上是一种分治算法,把原来的大问题,细分为一个个的小问题。这样小问题便于求解。
汉诺塔问题
递归的算法

归并排序
冒泡排序,插入排序,选择排序三者的时间复杂性是O(N^2)
归并排序的时间复杂性是O(N*lgN),显然它比前面几个都要快,但是归并排序有一个缺点
需要较大的存储空间。
归并两个有序数组
归并算法的中心是归并两个各自有序的数组,将其合成一个全新的按大小顺序排列的数组。
一般的归并排序,两个指针指向各自的元素,小的进来,指针后移。直到其中一方数据为空。复制另一方剩余的数据。


通过归并进行排序

