20199103 2019-2020-2 《网络攻防实践》期末大作业
论文介绍
我阅读的文章是ICSE2020的“Ankou: Guiding Grey-box Fuzzing towards Combinatorial Difference ”,作者是Valentin J.M. Manès,Soomin Kim和Sang Kil Cha,文章的主要内容是提出了一个新的灰盒测试工具。
最近模糊测试技术变得越来越热门。模糊测试不需要测试者进行太多的设置,测试者所需要设置的仅仅有两点:模糊测试的入口,以及测试的初始种子集。在测试过程中,种子需要根据实际的测试情况来动态的添加或者删除。在灰盒模糊测试中,会定义一个适应度函数,来决定某个种子是否适合添加到种子池之中。
现在大多数适应度函数都是基于代码覆盖率来构建适应度函数。例如:一个适应度函数是基于分支覆盖率,那么如果某个测试实例输入之后运行了之前从未运行过的分支,那么这个适应度函数就会将其加入种子池之中。尽管在实际实现的时候每个模糊测试器的适应度函数都各不相同,但是基本上都是倾向于将可以导致新的代码覆盖的输入加入到种子池之中。
尽管说这种适应度函数背广泛认可,但是还是有着他不可避免地缺陷。很多又bug的代码片段并不会每次在我们执行这片代码的时候都会发生,比如缓存区溢出bug。这样就导致基于代码覆盖率的适应度函数出现了缺陷,如果我们第一次执行这片代码的时候没有出现bug,而相应的输入又被添加到了种子池当中,那么下一次我们某个输入有可能回触发bug,但是这个输入的代码覆盖与我们之前添加进种子池的输入的代码覆盖完全一样,或者不完全一样但是没有产生新的代码覆盖,那么这个导致bug的输入就不会添加到种子池之中。
在文章中,提出了上述问题解决方面的三个困难:C1、想要区别各个输入测试用例,那么我们的适应度函数就必须能够量化不同的输入导致的程序执行上的差异。C2、在保证适应度函数可以提供足够的信息的同时,效率不能过低。C3、适应度函数需要保证种子池内不能有太多的种子,否则会难以处理。
C1不仅是一个需要解决的问题,还是本篇文章创新的核心。为了解决C1,作者引入了一种“基于距离”的适应度函数,它通过衡量两次程序的分支组合来量化这两个程序的相似度。这样以来,即使两次执行有着相同的代码覆盖,我们也能够在一定程度上对他们进行区别。但是这样又导致了另一个问题,就是计算量过大。根基作者的测试,直接采用基于距离的适应度函数会导致速度下降了13.2倍,这也就是我们上面所说的C2问题。问了应对计算量过大的问题,作者提出了一种降维方法动态PCA(principal component analysis,主成分分析)。这是在PCA之上进行改进的一种方法。之所以不直接采用PCA进行降维来降低计算所耗时间,是因为PCA本身所耗的时间就很多。而根据作者的调查,如今的所有PCA的延申变体都不满足需求,所以作者提出了动态PCA这个新概念,其核心思想就是让PCA的计算可以在上一次PCA计算的基础之上进行计算,避免了重复使用PCA造成的大量时间消耗。当然,使用降维就一定会或多或少的造成信息损失。根据作者的统计,使用动态PCA来降低基于距离的适应度函数的计算时间会造成大约18%的信息损失,但是效率却会大幅上升,总体而言利大于弊。最后就是种子池问题C3,种子池肯定不能无限制的大,不然我们可以直接把所有运行实例当作种子加进去。根据作者的测试,不对种子池做任何调整的话种子池就会过大导致程序无法运行。本文作者采用的方法就是定一个“阈值”来决定是否将程序实例纳入种子池当中,但是这个阈值时根据模糊测试器的运行结果而不断的修改的。并且当种子池的种子达到一定的数量之后,每加入一个种子就会挑选一个“最没用”的种子剔除。
基础知识
适应度与局部最优问题
根据上文所说,有些适应度函数选取种子的时候可能会忽略某些没有实现新的代码覆盖率的关键程序运行实例,我们把这种问题叫做局部最优问题。为了解决这个问题,有人提出了基于“分支命中次数”的适应度函数,核心思想是不再仅仅统计一个程运行实例分支覆盖,而是统计该运行实例在各个分支上的运行次数。这样以来即使两个程序运行实例有着相同的代码覆盖,但是我们通过统计每个分支的运行次数也可以将其量化的区分开。这样以来,对于每个程序实例的输出,我们就可以用一个向量x=(x1,x2,...,xn)T来表示出来,其中n代表程序的分支数总数。但是即使这样,还是会存在局部最优问题,例如下面三个程序运行实例的输出$x1=(1,1,2),x2=(1,1,0),x3=(0,1,2)。$这样以来,适应度函数就会选择x1而忽视x2,x3,因为他们相较x1没有产生新的分支覆盖,并且在产生分支数覆盖的分支数内的运行次数与x1完全相同。
PCA(主成分分析)

上图是30个程序运行实例的结果,每个点代表一个,两个维度分别代表两个分支的运行次数。PCA的目的是降维,也就是将上述的二维降成一维,同时保证这个30个点一维的空间上投影的方差最大。由于PCA的详细介绍不是这篇文章的创新点与重点,所以可以将PCA理解为一种降维工具,在本文中的具体作用是:PCA : (B, Σ) → (B′, Σ′)。其中B代表一组基,由于本文中的程序运行实例的结果都是用向量表示,所以B在本文中是一个矩阵,而Σ代表协方差矩阵。由于PCA的降维作用,所以在B′中每一个列向量都是线性无关的,一般情况下列向量的个数也会比B少。
基于距离的适应度函数
这一部分我认为是这篇论文创新的核心,也是解决C1问题的关键。C1问题要求我们建立一个可以准确的衡量不同程序测试实例之间的差异的适应度函数。在上文我们知道,已经有人将分支数的运行次数统计为向量用以区分不同的测试实例。作者认为这种统计方法已经提供了足够的多的信息,并将实现相同覆盖但是分支命中次数不同的两个程序将分别用各自相应的向量表示出来,然后对他们的距离进行统计。也就是说,与上文中的采用分支命中状态的适应度函数相比较,我们对程序测试实例有着更严格的区分,只要向量中有一个元素不同,我们就将这两个程序运行实例看作两个完全不同的实例,不会认为某个包含于某个。
首先我们给出一个程序的分支命中数的空间。对于一个程序p,我们定义 Ωp代表程序执行结果所有可能的分支命中数所组成的集合。然后我们考虑两个不同的程序测试运行实例的距离的概念,在基B下,我们将两个不同程序测试实例记作向量x,y,将距离其简单的定义为欧几里得距离||xT B − yT B||。依托距离,我们可以简单的量化两个不同的程序测试实例之间的相似程度。例如,三个不同的程序测试实例得到了三个不同的测试结果:(3,0,1),(3,0,0),(0,1,1)。很显然,我们的“距离”的概念下,第一个测试结果与第二个测试结果是颇为相近的,但是他们与第三个测试结果就相差不少了。
有了“距离”的概念,我们就可以对程序测试实例是否有资格加入种子池这个问题进行量化,也就是写出适应度函数。在已有一个种子池Π = {t1,t2, ... ,tm }的时候,对于一个新的测试实例t,我们要测试这个实例域种子池之间的距离,就需要将t与种子池中的每一个种子之间的距离计算出来,然后取当中的最小值当作t与种子池之间的距离。例如在程序p之下的一个测试运行实例t,我们将t的分支命中的向量用ϵ表示,然后在一个基B之下,对于t与种子池的距离,我们就可以写作:$∆B(t, Π) = mini∈ΠδB(ϵp (t), ϵp (i))$。当我们计算出实例域种子池之间的距离的时候,适应度函数的任务就完成了,之后就要判定这个实例有没有资格加入种子池,这就是种子池调整的任务了。
但是这样以来我们就面临一个很严重的问题,就是计算量太多庞大,对于每个测试用例我们都需要计算他与种子池之间的距离。这个计算的复杂度大概是O(mn),这里m代表种子池之中种子的个数,n代表分支的个数,而分支的个数很可能会非常大。所以我们就需要解决C2问题。
动态PCA
为了解决适应度函数的计算量过大的问题,我们引入了动态PCA,用以降低分支命中的维度,也就是不同分支的运行次数之间可能会存在某种相关关系,我们运用动态PCA就可以利用这一点来降维。标准的PCA在这里不适用的原因有的两点,其中一点就是我们之前所说的其本身的时间消耗就过大,其次就是每次我们的种子池更新的时候,我们的采样的概率分布就会发生变化,这样以来我们直接采用PCA的时间消耗就会更高了。
以下为动态PCA的算法。

可以看到动态PCA主要有三部分组成,ExpandBasisIfInteresting, UpdateCovMatrix, 和 PeriodicDecompose。
ExpandBasisIfInteresting其实是就是对测试运行实例的检查,检查是否“有资格”添加到基B之中,如果说无视改测试运行实例的话,会损失较大的信息,就对B进行更新。信息的损失计算在下面的algorithm1中有提及。
然后UpdateCovMatrix是更新协方差矩阵,如果基B添加了新的基,自然也需要更新协方差矩阵。但是要更新协方差矩阵我们就要面临一个问题,PCA是假设我们的抽样一直在一个恒定的概率分布,但是灰盒测试的过程显然不是这样,这里作者给出了一个折中方案Σ′=((xTB)(xTB)T+αwsΣ)/(1+αws),其中ws== 1+α+α2 +...+αs-1,α代表使用者的倾向程度,位于0到1之间,倾向0则代表使用者希望忽视过去的概率分布,倾向1则代表希望延续之前的概率分布。
PeriodicDecompose则是定期运行PCA来对B进行降维。这个定期一般是一分钟一次,但是也可以调整。需要注意的是这个输入的B是在之前调整过的,所以输入的B中的分支的个数要比实际运行测试中输出的分支的个数要少,这也进一步减少了计算所消耗的时间。
采用降维就代表着一定会造成信息流失。在作者的实际实验的过程中,信息的损失一直都没有超过20%。
自适应种子池调整
在之前有提到过,这个作者所采用的方法是设定一个阈值,然后计算新测试实例与种子池之间的所有的种子的距离的最小值,如果这个最小值大于阈值,九八这个测试实例的输入添加到种子池之中。这样以来,最关键的问题就是应该怎么样设置阈值。
通过下面的algorithm2我们可以看到,对于每个虚拟的测试实例添加进种子池的过程的最后一步都会更新阈值,而更新之后的阈值就是种子池之间所有种子之间的距离的最小值。而下一个测试实例与种子池之间的距离只要大于这个阈值,就会被添加到种子池之中。但是其实第4行的AddToPool不仅仅是添加种子到种子池,为了保证种子池不会过大,还会删除一个种子,删除的这个种子就是与新加入的种子距离最近的种子。但是种子池不仅仅要保证不能过大,还要保证不能过小,所以删除种子这一步只有在种子池中的种子大于1000个的时候才会进行。

Ankou的架构
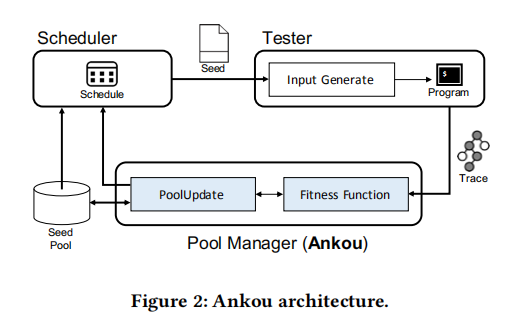
Ankou和一般的灰盒相似,主要有种子调度模块、种子池管理器模块和测试模块组成。种子调度模块选择一个种子并将其传递给测试模块,测试模块通过改变给定的种子来生成输入,运行程序。之后测试模块会将程序运行实例的结果(各个分支的运行次数)传递给种子池管理模块的适应度函数,然后种子池管模块就会动态的更新种子池。
实验结果
降维的影响
这一部分的实验主要是证明PCA在Ankou中是否真的有必要。
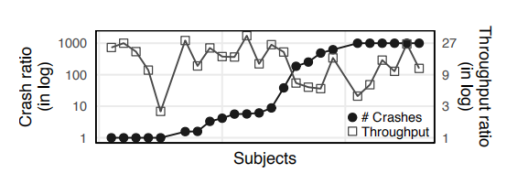
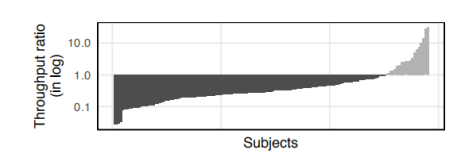
作者在这里创造了两种Ankou,一种是按照上面所描述的正常的Ankou,一种是没有动态PCA的Ankou,然后分别用这两种Ankou在相同的实验环境下对相同的程序组测试24小时,下图是测试结果。
其中黑色的圆圈代表在各个程序中,两种模式的Ankou发现的程序崩溃的bug的比例,白色的方形代表两种模式的Ankou的吞吐量的比例。通过下图我们可以清楚的看到,在吞吐量方面,采用动态PCA的Ankou远远优于不采用动态PCA的Ankou;在发现崩溃数量的方面,有五个程序上两个Ankou的表现相同,而其他的程序也都是采用动态PCA的Ankou更胜一筹。
动态PCA的负面影响
我们知道动态PCA在提升速度上有着很高的作用,但是也会造成信息损失。那么我们就需要知道,采用动态PCA会损失多少信息?换句话说,我们的动态PCA在降维的时候,能不能保证降维之后的维度是最大方差的呢?
作者选取了150个程序来进行测试,并通过计算基B的协方差矩阵Σ′来计算所损失的信息。结果如下图所示:
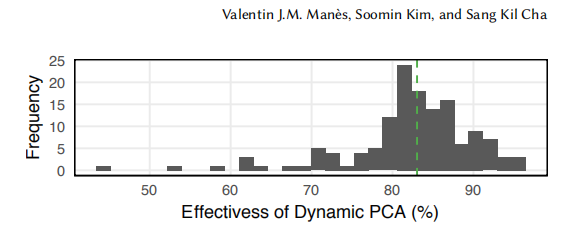
根据作者的测试结果,大约有80%的程序保留了78.8%以上的信息,有90%的程序保留了72.7%以上的信息。相较于提升的效率来说,可以说动态PCA利大于弊。
基于距离的适应度函数的增益
作者之所以提出基于距离的适应度函数,是因为基于代码覆盖的适应度函数不能提供足够的用于寻找bug的信息,但是我们也知道基于距离的适应度函数会造成运行效率降低。所以有必要对两种适应度函数的实际的运行进行对比。
作者对24个程序分别用两种函数进行测试,总体而言,基于距离的适应度函数所发现的崩溃bug的种类是基于代码覆盖率的函数的1.5倍,最高的程序甚至达到了4倍。而那些崩溃bug的种类对比不是很明显的程序,基于距离的适应度函数在83%的情况下都会输出更多的崩溃的数量。所以基于距离的适应度函数是更具有潜力的。
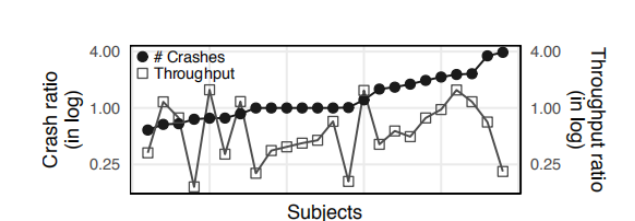
不过我们也可以看出,在吞吐量方面基于距离的适应度函数占有显著的劣势,因为计算所好的时间过长。但是即使这样,基于距离的适应度函数仍然能够找到更多的崩溃。
还有一点值得注意的是,两者在分支的覆盖率上差异很少,一直在1.5%以下,这也更进一步证明了作者在开始提出的猜想。
因此我们可以得出结论:基于距离的适应度函数更有效率。
动态PCA与标准PCA
因为标准PCA本身的运行时间过长,所以作者采用了动态PCA,那么如果使用了标准PCA会有多慢?
根据作者的实验,如果采用标准PCA,计算5000个种子文件就需要一个小时,但是模糊测试常常会每秒运行数千个测试实例,所以标准PCA可以说完全不可用。
基于距离的适应度函数在动态PCA下
我们知道基于距离的适应度函数在效率上会有所下降,那么采用动态PCA于其结合之后效率会怎么样?作者将Ankou与AFL进行对比,结果如下图。
可以看到,Ankou的速度整体上比AFL慢出不少。作者统计,整体上Ankou的速度要慢35%,并且在89%的情况下Ankou的速度都要慢。不过需要注意,尽管如此,在接下来我们可以看到Ankou发现的有意义的测试实例是AFL的两倍。
与其它模糊测试工具的对比
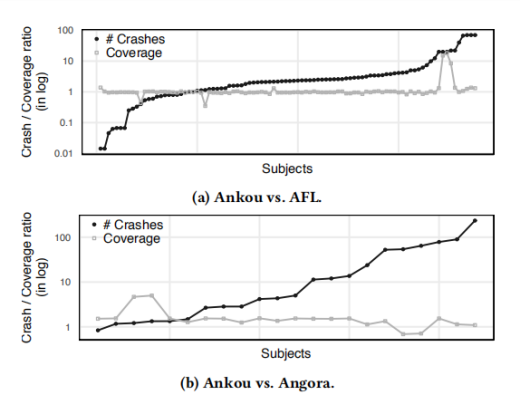
作者将Ankou与AFL、Angora进行了性能的对比。
对比之后发现,Ankou发现的崩溃数量大约是AFL的1.94倍,在75%的情况下都可以发现比AFL更多的崩溃。而在于Angora的对比中,Ankou发现的崩溃的数量大约是其8倍。
作者设计并实现了一种灰盒模糊测试工具Ankuo,用极高的维度提供了大量的信息,但是由于信息太多难以用于实践,所以提出了一种适用于Ankou的降维方法:动态PCA,之后又提出了与基于距离的适应度函数相适应的种子池管理方法,与其他的已有的模糊测试工具相比,可以说是极大的提升了bug的查找能力。
复现
作者在github上公开了Ankou的源代码。作者是用go语言编写的Ankou,所以在复现之前需要配置go语言的环境。并且Ankou需要AFL里的fuzzed工具,所以还需要配置AFL。但是AFL不能在windows上运行,而AFL的win版本WinAFL我经过多次尝试都以失败结果。所以最终的实验我是在虚拟机KALI上完成的。
作者在github中的源代码中不仅公开了源代码与测试用程序,而且在readme部分对环境的配置也有着很详细的描述。
虽然作者公开了全部的测试程序,但是由于作者的实验是在较好的环境下运行数十小时得出的数据,而我的虚拟机环境较差,并且我的笔记本页承受不起数十小时的运转,所以我无法做到和作者完全一样的测试。
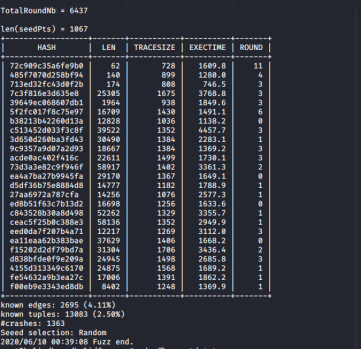
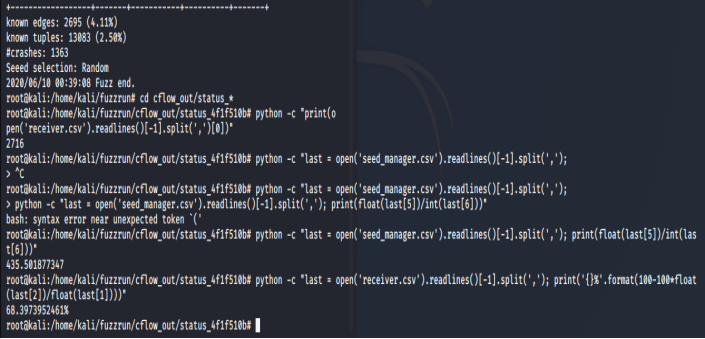
下图为我用Ankou对作者公开的测试用程序进行了两个小时测试的结果。
从测试结果可以看出,我的测试总共找到了1363个崩溃bug,覆盖了2716个分支,总吞吐量为435.501877347,动态PCA提升的效率约为68%。
课程总结与课程建议
从我一个本科跨专业上研究生来学这门课的学生的角度而言,学习过程真的挺吃力的。有大量的基础知识欠缺,所以在整个学习过程中几乎都在补课。从数据库到汇编,从网络协议到linux,有以前自学过的内容,也有从未接触过的,因为需要补充的知识太多,所以我也只能本着实用主义的原则,用到什么学什么。并且这门课的实践要求也是很高,一学期里我接触了太多之前闻所未闻的东西。最可惜的一点就是直到最后我对好多的原理还是一知半解。总的来说自我感觉进步不小,但是也只能说差强人意。
在建议上,我认为应该多增加交流的机会,尽管说实践终归是要自己动手才能理解,但是在实验的时候经常会卡在某个点做不下去实验或者难以理解,这时候别人的一个小指点真的能事半功倍。