图像处理------ 一阶微分应用 分类： 视频图像处理 2015-07-24 10:07 38人阅读 评论(0) 收藏

一：数学背景

首先看一下一维的微分公式Δf = f(x+1) – f(x), 对于一幅二维的数字图像f(x,y)而言，需要完

成XY两个方向上的微分，所以有如下的公式：

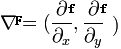
分别对X,Y两个方向上求出它们的偏微分，最终得到梯度Delta F.

对于离散的图像来说,一阶微分的数学表达相当于两个相邻像素的差值，根据选择的梯度算

子不同，效果可能有所不同，但是基本原理不会变化。最常见的算子为Roberts算子，其它

常见还有Sobel，Prewitt等算子。以Roberts算子为例的X,Y的梯度计算演示如下图：

二：图像微分应用

图像微分(梯度计算)是图像边缘提取的重要的中间步骤，根据X,Y方向的梯度向量值，可以

得到如下两个重要参数振幅magnitude, 角度theta，计算公式如下：

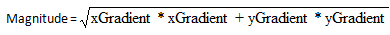
Theta = tan^-1(yGradient/xGradient)

magnitude表示边缘强度信息

theta预言边缘的方向走势。

假如对一幅数字图像，求出magnitude之后与原来每个像素点对应值相加，则图像边缘将被

大大加强，轮廓更加明显，是一个很典型的sharp filter的效果。

 

三：程序效果

X, Y梯度效果，及magnitude效果

图像微分的Sharp效果：

四：程序源代码

package com.process.blur.study;

import java.awt.image.BufferedImage;

// roberts operator
// X direction 1, 0
//             0,-1
// Y direction 0, 1
//            -1, 0

public class ImageGradientFilter extends AbstractBufferedImageOp {
    public final static int X_DIRECTION = 0;
    public final static int Y_DIRECTION = 2;
    public final static int XY_DIRECTION = 4;

    private boolean sharp;
    private int direction;

    public ImageGradientFilter() {
        direction = XY_DIRECTION; // default;
        sharp = false;
    }

    public boolean isSharp() {
        return sharp;
    }

    public void setSharp(boolean sharp) {
        this.sharp = sharp;
    }

    public int getDirection() {
        return direction;
    }

    public void setDirection(int direction) {
        this.direction = direction;
    }

    @Override
    public BufferedImage filter(BufferedImage src, BufferedImage dest) {
        int width = src.getWidth();
        int height = src.getHeight();

        if (dest == null )
            dest = createCompatibleDestImage( src, null );

        int[] inPixels = new int[width*height];
        int[] outPixels = new int[width*height];
        getRGB( src, 0, 0, width, height, inPixels );
        int index = 0;
        double mred, mgreen, mblue;
        int newX, newY;
        int index1, index2, index3;
        for(int row=0; row<height; row++) {
            int ta = 0, tr = 0, tg = 0, tb = 0;
            for(int col=0; col<width; col++) {
                index = row * width + col;

                // base on roberts operator
                newX = col + 1;
                newY = row + 1;
                if(newX > 0 && newX < width) {
                    newX = col + 1;
                } else {
                    newX = 0;
                }

                if(newY > 0 && newY < height) {
                    newY = row + 1;
                } else {
                    newY = 0;
                }
                index1 = newY * width + newX;
                index2 = row * width + newX;
                index3 = newY * width + col;
                ta = (inPixels[index] >> 24) & 0xff;
                tr = (inPixels[index] >> 16) & 0xff;
                tg = (inPixels[index] >> 8) & 0xff;
                tb = inPixels[index] & 0xff;

                int ta1 = (inPixels[index1] >> 24) & 0xff;
                int tr1 = (inPixels[index1] >> 16) & 0xff;
                int tg1 = (inPixels[index1] >> 8) & 0xff;
                int tb1 = inPixels[index1] & 0xff;

                int xgred = tr -tr1;
                int xggreen = tg - tg1;
                int xgblue = tb - tb1;

                int ta2 = (inPixels[index2] >> 24) & 0xff;
                int tr2 = (inPixels[index2] >> 16) & 0xff;
                int tg2 = (inPixels[index2] >> 8) & 0xff;
                int tb2 = inPixels[index2] & 0xff;

                int ta3 = (inPixels[index3] >> 24) & 0xff;
                int tr3 = (inPixels[index3] >> 16) & 0xff;
                int tg3 = (inPixels[index3] >> 8) & 0xff;
                int tb3 = inPixels[index3] & 0xff;

                int ygred = tr2 - tr3;
                int yggreen = tg2 - tg3;
                int ygblue = tb2 - tb3;

                mred = Math.sqrt(xgred * xgred + ygred * ygred);
                mgreen = Math.sqrt(xggreen * xggreen + yggreen * yggreen);
                mblue = Math.sqrt(xgblue * xgblue + ygblue * ygblue);
                if(sharp) {
                    tr = (int)(tr + mred);
                    tg = (int)(tg + mgreen);
                    tb = (int)(tb + mblue);
                    outPixels[index] = (ta << 24) | (clamp(tr) << 16) | (clamp(tg) << 8) | clamp(tb);
                } else {
                    outPixels[index] = (ta << 24) | (clamp((int)mred) << 16) | (clamp((int)mgreen) << 8) | clamp((int)mblue);
                    // outPixels[index] = (ta << 24) | (clamp((int)ygred) << 16) | (clamp((int)yggreen) << 8) | clamp((int)ygblue);
                    // outPixels[index] = (ta << 24) | (clamp((int)xgred) << 16) | (clamp((int)xggreen) << 8) | clamp((int)xgblue);
                }


            }
        }
        setRGB(dest, 0, 0, width, height, outPixels );
        return dest;
    }

    public static int clamp(int c) {
        if (c < 0)
            return 0;
        if (c > 255)
            return 255;
        return c;
    }
}

版权声明：本文为博主原创文章，未经博主允许不得转载。