本文讲述java中基本数据类型溢出的原理,在此之前,我们要先了解一下计算机补码的知识。
一、用补码表示数
计算机中,将补码作为实际数据的存储形式,其中正数的补码与原码(原始二进制编码)相同,负数的补码是在保持最高符号位不变的情况下将其余比特位按位取反,然后再加上1。以127和-127为例,它们的原码、补码计算过程如下:
| 127 | -127 | |
| 原码 | 0111 1111 | 1111 1111 |
| 补码 | 0111 1111(正数补码与原码相同) | 1000 0000(最高位不变,其余位按位取反) |
| 1000 0001(最低位加1) |
对于计算机来说,补码的优势是可以让减法运算变成加法运算,举个例子,127-127可以变成127的补码加上-127的补码,这直接减少了CPU设计的复杂度(减法指令直接用加法指令代替)。
二、基本数据类型的取值范围
以byte为例,java中的byte是一个字节,在给出它真实的取值范围之前,让我们先运用学到的补码知识,尝试写出最大值和最小值:
| 二进制原码 | 二进制补码 | 十进制表示 | |
| 最小值 | 1111 1111 | 1000 0001 | -127 |
| 最大值 | 0111 1111 | 0111 1111 | +127 |
可以看到,我们认为byte的最大值为+127,最小值为-127,然而在java规范中,定义的byte取值范围是[-128, 127],这个-128从何而来?实际上,它只是java的一个特殊处理,为了理解这一点,先看两个特殊的0值:
| 二进制原码 | 二进制补码 | |
| +0 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1 0000 0000 |
(1)整数集中,是不存在所谓-0的,映射到计算机世界时,也不应该存在-0。
(2)对于-0这个数,它的二进制补码产生了进位,由于byte只有8位,进位的1将被会舍弃,那么它的补码就变成0000 0000,这样一来,负数变成了正数,符号产生了颠倒。
如果简单的删除-0这个数,就可以完美解决上面两个矛盾,但java并未采取这个做法,而是选择将-0这个数映射成-128,并且由于-0的补码会产生进位,所以让其补码与原码相同,如下表所示:
| 二进制原码 | 二进制补码 | |
| 0 | 0000 0000 | 0000 0000 |
| -128 | 1000 0000 | 1000 0000 |
以上的推导也适用于其他整数类型,比如short、int、long,而char类型由于只包含自然数,就不存在这么复杂的处理了。
三、基本数据类型的溢出
还是以byte类型为例,有了上面了解到的知识,我们很容易的推理出数据是如何溢出的。
1 public static void main(String[] args) {
2 byte b = -128;
3 System.out.println((byte)(b - 1));
4 byte b1 = 127;
5 System.out.println((byte)(b1 + 1));
6 }
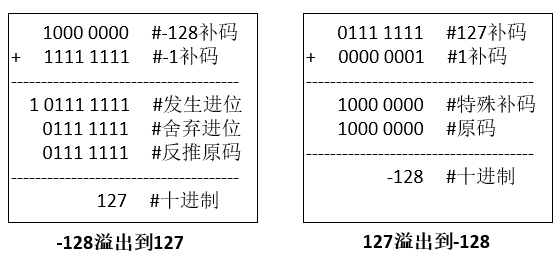
最小值-128继续减少1,发生溢出,得到结果127;最大值127继续增加1,发生溢出,得到结果-128: