本讲内容
1.Optional margin classifier（最优间隔分类器）
2.primal/dual optimization（原始优化问题和对偶优化问题）KKT conditions（KKT条件）
3.SVM dual （SVM的对偶问题）
4.kernels （核方法）
1.最优间隔分类器
对于一个线性可分的训练集合，最优间隔分类器的任务是寻找到一个超平面(w,b), 使得该超平面到训练样本的几何间隔最大。
你可以任意地成比例地缩放w和b的值，这并不会改变几何间隔的大小。
例如，我可以添加这样的约束：
这意味着我可以先解出w的值，然后缩放w的值，使得 
我们可以自由地选择缩放因子来添加一些约束条件，但不会改变几何间隔的大小。
考虑最优间隔分类器的优化问题：
添加 
这个条件，可以使几何间隔等于函数间隔。但是这个条件是一个非常糟糕的非凸性约束，所以需要改变优化问题：
实际上这依然是一个糟糕的非凸性优化目标，很难找到参数的全局最优解。之前说过我们可以自由地选择缩放因子来添加一些奇怪的约束条件，这里我们选择添加 
.很明显这是一个缩放约束，当解出w，b的值后，你可以对他们进行任意地缩放，使得函数间隔等于1.因此优化问题变为：
这就是最终的凸优化问题。
2.原始问题和对偶问题
拉格朗日乘数法
假设有一个优化问题
首先创建一个拉格朗日算子
其中 
称为拉格朗日乘数。
令参数的偏导数为0：
解方程组，求得w为最优解。
拉格朗日乘数法的扩展形式
假设有一个优化问题，称为原始问题p
首先创建一个拉格朗日算子
接着定义
当约束条件满足的时候，即 
否则，任一约束不满足
考虑这样的优化问题
实际上等价于原始问题p
对偶问题：
定义
考虑这样的优化问题
这就是对偶问题。注意到对偶问题和原始问题的区别是，对偶问题的求最大值和求最小值的顺序刚好和原始问题相反。
一个事实是 
.即最大值的最小值一定大于最小值的最大值。
在特定条件下，原始问题和对偶问题会得到相同的解。因此满足某些条件时，可以用对偶问题的解代替原始问题的解。
通常来说，对偶问题会比原始问题简单，并且具有一些有用的性质。
使原始问题和对偶问题等价的条件：
令f为凸函数 (Hessian H>=0)
假设 
是仿射函数 
接着假设 
严格可执行 
（注意是小于，而不是小于等于）
所以，
， 使得 
是原始问题的解，
是对偶问题的解，并且 
KKT(Karush-kuhn-Tucker)互补条件：
(1) 
(2) 
(3) 
(4) 
(5) 
根据条件(3)，一般情况下 
这不是绝对成立的，因为可能两个值都为0.
当 
成立时，我们称 
是一个active constraint（活动约束）。
3.最优间隔分类器 对偶问题
原始问题
约束为
这是一个活动约束
当 
意味着训练样本 
的函数间隔等于1.
从上图可以看出，通常情况下，一个最优化问题的解只和特别少的样本有关。例如，上图的所有点中，只有离超平面分隔线最近的三个点，他们的函数间隔为1，拉格朗日乘数不为0，这三个样本我们称之为支持向量(support vectors)
拉格朗日算子
对偶问题为
为了求解对偶问题，我们需要对w，b求偏导数，并令偏导数为0 得到拉格朗日算子取极小值时的w,b。
将上述两条约束代入拉格朗日算子
因此对偶问题可以描述为
求解上述对偶问题，解出 
，那么
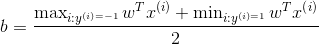
我们可以将整个算法表示成内积的形式
4.核方法
在SVM的特征向量空间中，有时候训练样本的维数非常高，甚至是无限维的向量。但是你可以使用 
来高效地计算内积，而不必把x显式的表示出来。
这个结论仅对一些特定的特征空间成立。
第七讲完。