方程的解数
| Time Limit: 15000MS | Memory Limit: 128000K | |
| Total Submissions: 6188 | Accepted: 2127 | |
| Case Time Limit: 5000MS | ||
Description
已知一个n元高次方程:
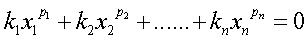
其中:x1, x2,...,xn是未知数,k1,k2,...,kn是系数,p1,p2,...pn是指数。且方程中的所有数均为整数。
假设未知数1 <= xi <= M, i=1,,,n,求这个方程的整数解的个数。
1 <= n <= 6;1 <= M <= 150。
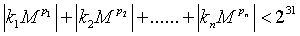
方程的整数解的个数小于231。
★本题中,指数Pi(i=1,2,...,n)均为正整数。
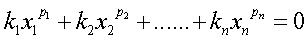
其中:x1, x2,...,xn是未知数,k1,k2,...,kn是系数,p1,p2,...pn是指数。且方程中的所有数均为整数。
假设未知数1 <= xi <= M, i=1,,,n,求这个方程的整数解的个数。
1 <= n <= 6;1 <= M <= 150。
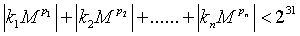
方程的整数解的个数小于231。
★本题中,指数Pi(i=1,2,...,n)均为正整数。
Input
第1行包含一个整数n。第2行包含一个整数M。第3行到第n+2行,每行包含两个整数,分别表示ki和pi。两个整数之间用一个空格隔开。第3行的数据对应i=1,第n+2行的数据对应i=n。
Output
仅一行,包含一个整数,表示方程的整数解的个数。
Sample Input
3 150 1 2 -1 2 1 2
Sample Output
178
#include<stdio.h> #include<stdlib.h> #define Max 4000037 int hash[Max],num[Max]; //hash判断和的位置,num是和为s的个数 bool used[Max]; bool used[Max]; //判断hash是否用过 int n,M,k[7],p[7],cnt,mid; int locat(int s) { int tmp=s; while(tmp<0) { tmp+=Max; } while(tmp>=Max) { tmp-=Max; } while(used[tmp]&&hash[tmp]!=s) { tmp++; if(tmp>=Max) { tmp-=Max; } } return tmp; } void in_sert(int s) { int pos=locat(s); hash[pos]=s; used[pos]=1; num[pos]++; } void left_dfs(int d,int s) //左边一半的值的和的可能 { if(d==mid) { in_sert(s); return ; } for(int i=1;i<=M;i++) { int tmp=k[d]; if(i!=1&&tmp!=0) { for(int j=0;j<p[d];j++) { tmp*=i; } } left_dfs(d+1,s+tmp); } } void right_dfs(int d,int s) //右边所有和的可能如果左右相等,那么就加上这个和的所有可能 { if(d==n) { s=-s; int pos=locat(s); if(hash[pos]==s) { cnt+=num[pos]; } return ; } for(int i=1;i<=M;i++) { int tmp=k[d]; if(i!=1&&tmp!=0) { for(int j=0;j<p[d];j++) { tmp*=i; } } right_dfs(d+1,s+tmp); } } int main() { int i,j; scanf("%d",&n); scanf("%d",&M); for(i=0;i<n;i++) { scanf("%d%d",&k[i],&p[i]); } mid=n/2; cnt=0; left_dfs(0,0); right_dfs(mid,0); printf("%d ",cnt); return 0; }