HDU 4570 Multi-bit Trie

Multi-bit Trie

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 180    Accepted Submission(s): 56

Problem Description

　　IP lookup is one of the key functions of routers for packets forwarding and classifying. Generally, IP lookup can be simplified as a Longest Prefix Matching (LPM) problem. That's to find the longest prefix in the Forwarding Information Base (FIB) that matches the input packet's destination address, and then output the corresponding Next Hop information.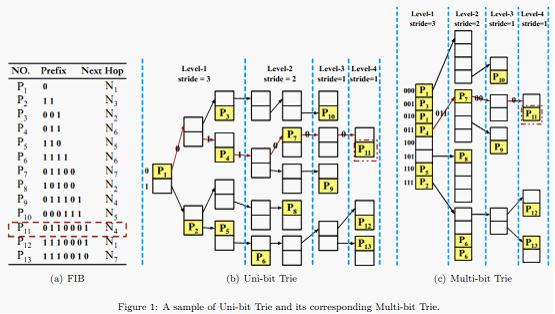　　Trie-based solution is the most wildly used one to solve LPM. As shown in Fig.1(b), an uni-bit trie is just a binary tree. Processing LPM on it needs only traversing it from the root to some leaf, according to the input packet's destination address. The longest prefix along this traversing path is the matched one. In order to reduce the memory accesses for one lookup, we can compress some consecutively levels of the Uni-bit Trie into one level, transforming the Uni-bit Trie into a Multi-bit Trie. 　　For example, suppose the strides array is {3, 2, 1, 1}, then we can transform the Uni-bit Trie shown in Fig.1(b) into a Multi-bit Trie as shown in Fig.1(c). During the transforming process, some prefixes must be expanded. Such as 11(P2), since the first stride is 3, it should be expanded to 110(P2) and 111(P2). But 110(P5) is already exist in the FIB, so we only store the longer one 110(P5). 　　Multi-bit Trie can obviously reduce the tree level, but the problem is how to build a Multi-bit Trie with the minimal memory consumption (the number of memory units). As shown in Fig.1, the Uni-bit Trie has 23 nodes and consumes 46 memory units in total, while the Multi-bit Trie has 12 nodes and consumes 38 memory units in total.

 

Input

　　The first line is an integer T, which is the number of testing cases. 　　The first line of each case contains one integer L, which means the number of levels in the Uni-bit Trie. 　　Following L lines indicate the nodes in each level of the Uni-bit Trie. 　　Since only 64 bits of an IPv6 address is used for forwarding, a Uni-bit Trie has maximal 64 levels. Moreover, we suppose that the stride for each level of a Multi-bit Trie must be less than or equal to 20.

 

Output

　　Output the minimal possible memory units consumed by the corresponding Multi-bit Trie.

 

Sample Input

1

7

1

2

4

4

5

4

3

 

Sample Output

38

 

Source

2013 ACM-ICPC长沙赛区全国邀请赛——题目重现

 

区间DP问题

此题最难的就是读懂题意（好吧，我承认我到AC了都没时白Discription里说的是啥...）

将题目转化过之后就是如下这个（据说）很水的区间DP问题：

一个长度为n的数列，将其分成若干段（每一段的长度要<=20），要求∑ai*(2^bi)最小，其中ai是每一段数列的第一项，bi是每一段的长度。

比如：n=7，A={1 2 4 4 5 4 3}，将其分成1 2 4| 4 5| 4| 3，则其所用空间为1*23+4*22+4*21+3*21=38，而如果分成1 2| 4 4 5| 4 3，则其所用空间为1*22+4*23+4*22=52，比38大。

 

#include<iostream>
#include<cstring>
#include<cstdio>

using namespace std;

long long num[65];
long long sum[65];
long long two[65];
long long dp[65][65];

long long min(long long a,long long b)
{
    return a<b?a:b;
}

int main()
{
    int t;

    scanf("%d",&t);

    two[0]=1;
    for(int i=1;i<=30;i++)
        two[i]=two[i-1]*2;

    while(t--)
    {
        int l;

        memset(sum,0,sizeof(sum));
        memset(dp,0,sizeof(dp));

        scanf("%d",&l);

        for(int i=1;i<=l;i++)
        {
            cin>>num[i];
            sum[i]=sum[i-1]+num[i];
        }

        for(int len=0;len<l;len++)
        {
            for(int i=1;i<=l&&i+len<=l;i++)
            {
                int j=i+len;
                //初始化，注意区间长度小于等于20的各大于20的不一样
                if(len<=19)
                    dp[i][j]=min((sum[j]-sum[i-1])*2,num[i]*two[len+1]);
                else
                    dp[i][j]=2*(sum[j]-sum[i-1]);
                //动规过程
                for(int k=i;k<j;k++)
                    dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
            }
        }

        cout<<dp[1][l]<<endl;
    }

    return 0;
}