20155239吕宇轩待及格加分项目
递归
一、基本概念
递归算法是一种直接或者间接调用自身函数或者方法的算法。Java递归算法是基于Java语言实现的递归算法。递归算法的实质是把问题分解成规模缩小的同类问题的子问题,然后递归调用方法来表示问题的解。递归算法对解决一大类问题很有效,它可以使算法简洁和易于理解。递归算法,其实说白了,就是程序的自身调用。它表现在一段程序中往往会遇到调用自身的那样一种coding策略,这样我们就可以利用大道至简的思想,把一个大的复杂的问题层层转换为一个小的和原问题相似的问题来求解的这样一种策略。递归往往能给我们带来非常简洁非常直观的代码形势,从而使我们的编码大大简化,然而递归的思维确实很我们的常规思维相逆的,我们通常都是从上而下的思维问题, 而递归趋势从下往上的进行思维。这样我们就能看到我们会用很少的语句解决了非常大的问题,所以递归策略的最主要体现就是小的代码量解决了非常复杂的问题。
递归算法解决问题的特点:
1)递归就是方法里调用自身。
2)在使用递增归策略时,必须有一个明确的递归结束条件,称为递归出口。
3)递归算法解题通常显得很简洁,但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。
4)在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等,所以一般不提倡用递归算法设计程序。
在做递归算法的时候,一定要把握住出口,也就是做递归算法必须要有一个明确的递归结束条件。这一点是非常重要的。其实这个出口是非常好理解的,就是一个条件,当满足了这个条件的时候我们就不再递归了。
①斐波纳契数列(Fibonacci Sequence)
问题描述:求解Fibonacci数列的第n个位置的值?(斐波纳契数列(Fibonacci Sequence),又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F1=1,F2=1,Fn=F(n-1)+F(n-2)(n>2,n∈N*))。
使用JDB调试Java程序
Linux Bash下打开三个标签页
如图所示:
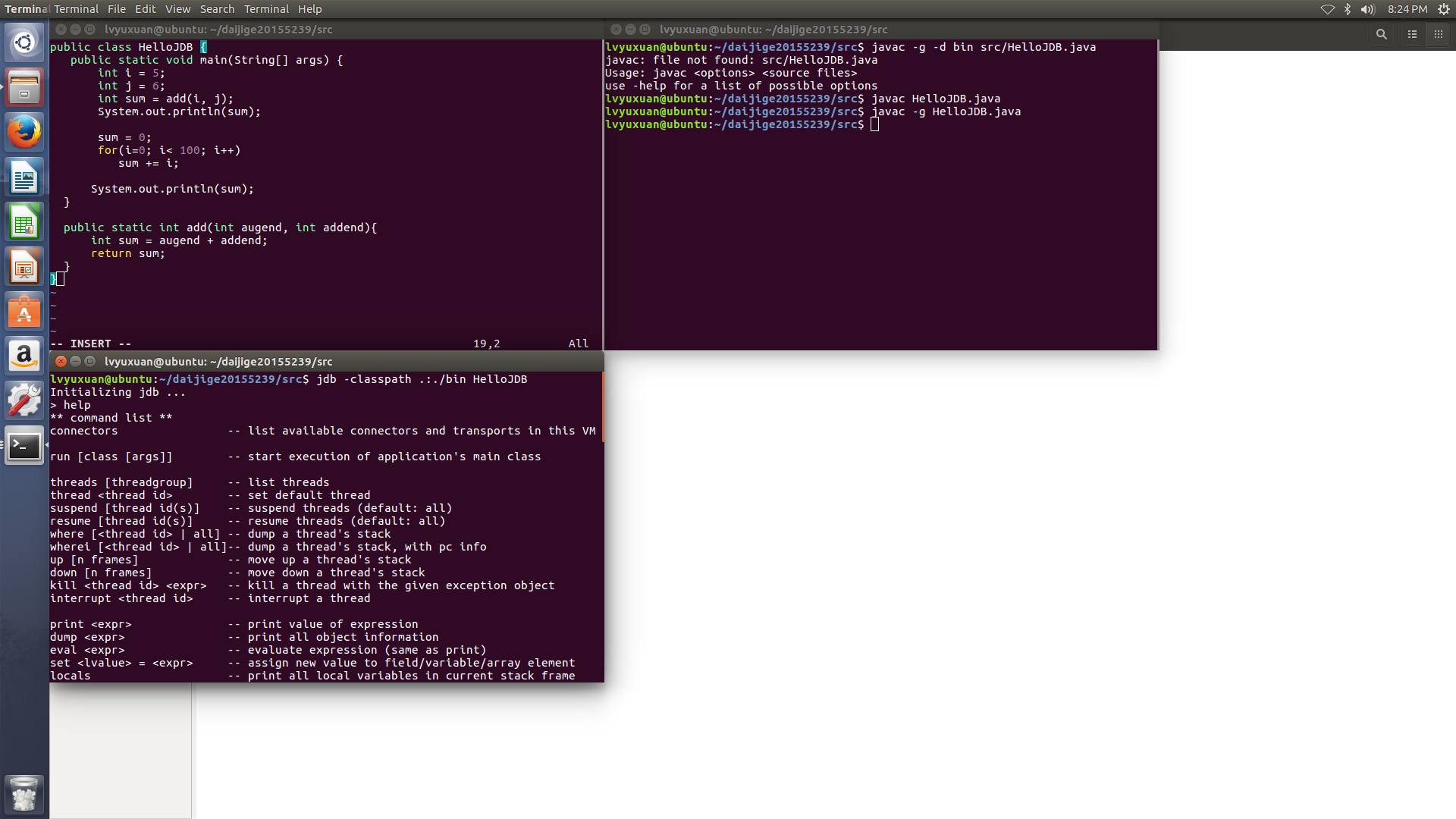
代码编辑完,我们按“:w”进行保存而不是“:wq”进行保存退出,这样在编译或调试中遇到问题就可以按Alt+1 进入第一个标签修代码了。
我们按Alt+2 进入第二个标签,使用javac -g -d bin src/HelloJDB.java对程序进行编译。注意javac中-g参数是为了产生各种调试信息,一定要加上,否则无法调试。
调试基础
调试程序先要学会设置断点,这样才能让程序停在你感觉有问题的代码处进行排查。学习调试我们要学会设置四种断点:
方法断点
行断点
条件断点
临时断点
我们在JDB中输入help可以查看命令列表:
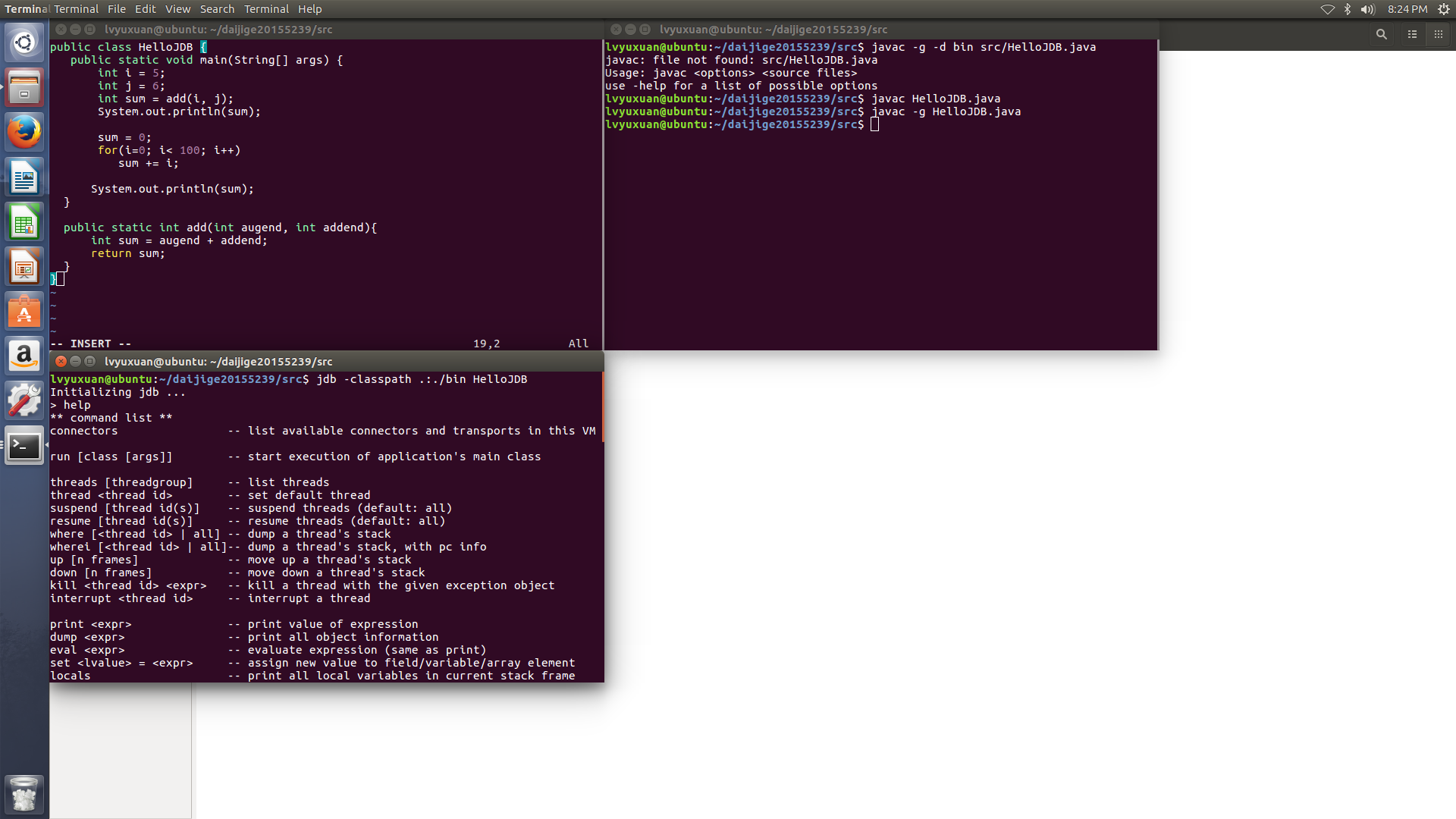
stop in
用来设置方法断点,
stop at
设置行断点。
我们通过运行
stop in
HelloJDB.main命令在main方法开始处设置断点:

输入run命令来运行HellJDB.class,程序会在main()的开始处停下。
locals命令查看变量,step命令运行下一行代码:

看两条locals命令的结果,开始只有main方法的参数args,后面就有局部变量i,j的值了。
使用print来查看值。

list来查看运行到了源代码的什么位置

继续输入step和list,我发现代码跳入16行方法体中

通过stop at HelloJDB:12在第12行设个断点,然后运行cont就会一下子把循环运行完并停在第十二行

15.cnblogs.com/blog/1074290/201705/1074290-20170530145226414-1343628620.png)