今天洛谷试练场看到斐波那契 发现我学矩阵乘法时死于玄学错误 最后放弃自我 然后决定搞一搞矩阵乘法
快速幂优化的矩阵乘法
1 matrix mul(matrix a,matrix b) 2 { 3 matrix c; 4 c.m[0][0]=c.m[0][1]=c.m[1][1]=c.m[1][0]=0;//初始化 5 for(int i=0;i<2;++i) 6 for(int j=0;j<2;++j) 7 for(int k=0;k<2;++k) 8 c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod; 9 return c; 10 } 11 12 void qpow(ll b)//快速幂 13 { 14 while(b) 15 { 16 if(b&1) ans=mul(ans,base); 17 base=mul(base,base); 18 b>>=1; 19 } 20 }
这题很水 很裸 就是模板题
值得了gai一下斐波那契通项公式 (虽然我也不晓得有什么用)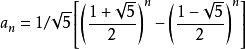
然后它深刻地教会我 什么叫 不开long long见祖宗

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int mod=1000000007; 5 ll n; 6 struct matrix {ll m[2][2];}base,ans; 7 template<class t>void rd(t &x) 8 { 9 x=0;int w=0;char ch=0; 10 while(!isdigit(ch)) w|=ch=='-',ch=getchar(); 11 while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); 12 x=w?-x:x; 13 } 14 15 matrix mul(matrix a,matrix b) 16 { 17 matrix c; 18 c.m[0][0]=c.m[0][1]=c.m[1][1]=c.m[1][0]=0;//初始化 19 for(int i=0;i<2;++i) 20 for(int j=0;j<2;++j) 21 for(int k=0;k<2;++k) 22 c.m[i][j]=(c.m[i][j]+a.m[i][k]*b.m[k][j])%mod; 23 return c; 24 } 25 26 void qpow(ll b)//快速幂 27 { 28 while(b) 29 { 30 if(b&1) ans=mul(ans,base); 31 base=mul(base,base); 32 b>>=1; 33 } 34 } 35 36 int main() 37 { 38 rd(n); 39 if (n <= 2) return puts("1"), 0; 40 base.m[0][0]=base.m[0][1]=base.m[1][0]=1,base.m[1][1]=0; 41 ans.m[0][0]=ans.m[1][1]=1,ans.m[0][1]=ans.m[1][0]=0; 42 qpow(n); 43 printf("%lld",ans.m[0][1]%mod); 44 return 0; 45 }
