Trust-Region-Methods
Trust-Region Method(置信域方法)利用目标函数在迭代点的函数值与导数信息来建立一个二次型模型用来近似表示目标函数,而在距离迭代点多远的范围之内可以相信这个二次型模型,这个范围就是置信域。
二次型模型
在迭代点的二次型模型具体表示为$$m_k(p)=f_k+ abla f_k^T p+ frac{1}{2}p^T B_k p$$式子中(f_k)是目标函数在第k个迭代点的取值,(B_k)是一个对称矩阵,一般来说,很容易想到它会是(x_k)点的Hessian矩阵,不过这里并不要求必须是Hessian矩阵,(B_k)的不同也导出了不同类型的方法。
算法大致过程
TRM在达到目标任务的过程中,一是要不断求解二次型模型的子问题,第二就是要适当地控制置信域,为此,考虑一个比值$$
ho_k = frac{f(x_k)-f(x_k+p_k)}{m_k(0)-m_k(p_k)}$$可以看见,分子是实际目标函数的下降量,而分母是二次型局部模型的下降量,(p_k)的选择必定使得分母是非负的,通过(
ho_k),能够知道根据局部模型做出的决定与真实函数情况有多少程度的符合。每次迭代计算相应的(
ho_k),并根据(
ho_k)来调整置信域。下面的伪代码是具体的设置。

算法的框架已经很明了了,现在剩下的问题是如何求解局部二次型子问题,即如何根据二次型模型得到一个(p_k)来尽量最小化二次型。
子问题求解
本章介绍的三个子问题近似求解方法都是基于Cauchy点的。
Cauchy点
(下面的(g_k)实际上是(
abla f_k),而(g)就表示(
abla f),意思是专注于同一个迭代步骤中的过程)

上图是Cauchy点的定义,抛开繁杂的符合定义,其实可以看出,Cauchy点就是梯度负方向上的二次型最低点,这样他的意义就明了很多。重要的是,Cauchy点有闭式解,不难得到:
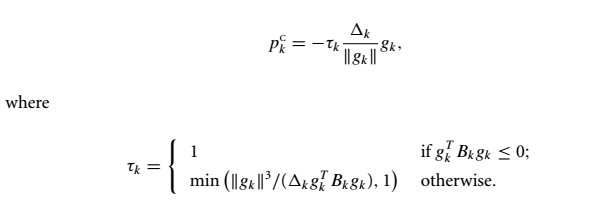
dogleg方法
如果置信域足够大,即(delta_k > |p^B|),其中(p^B=-B^{-1}g)是二次型的全局最优点。而置信域不够大的时候,二次型中二次项的影响会很小,此时将二次型的二次项直接忽略,只根据一次项的信息来决定优化点,那么随着(delta_k)的增大,优化点的轨迹显然是从中心到Cauchy点的连线。dogleg方法就是简单的折中了,从下图可以看的很明白。
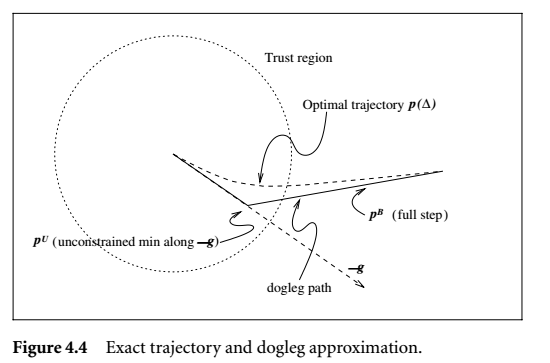
dogleg方法需要(B_k)是正定的,在这样的条件下,置信域与优化轨道只有一个交点,并且顺着优化轨道,(m_k)单调递减。
Two-Dimension Subspace方法
这种方法书上介绍的很不详细,大致上是在梯度方向和全局点方向张成的二维子空间中优化(m_k),即$$min limits_p m(p)=f+gTp+frac{1}{2}pTBp quad s.t.|p| leq delta,pin span left[g,B^{-1}g ight]$$
Steihaug's approach
是一种对共轭梯度法的改进,这里不再细说。
精确求解子问题
对二次型,有下面的非常有用的结论

有了这个结论,我们可以用牛顿法来寻找(lambda)的取值,从而得到非常精确的子问题最优解点。
具体过程的话,首先将对称矩阵(B)做分解化为标准型,即(B=QLambda Q^T),根据第一个条件,定义$$p(lambda)=-(B+lambda I){-1}g=-sum_{j=1}n frac{q_j^Tg}{lambda_j+lambda}q_j$$(q_j)是Q的第(j)个列向量。设(lambda_1)是B最小的特征值,那么$$limlimits_{lambda
ightarrow infty}|p(lambda) = 0$$如果(q_j^TB
eq 0)$$limlimits_{lambda
ightarrow lambda_j} |p(lambda)|=infty$$于是可以用牛顿法求解$$|p(lambda)-Delta |=0$$
当(q_1^Tg=0),情况就要复杂一些,此时可能在((lambda_1,infty))内没有解,如果没有解,又由条件3,(lambda)只能取(lambda_1),此时将(p(lambda_1))稍做修改,让他加上一个与(B-lambda_1I)正交的单位向量,条件一不被破坏,但使得我们可以通过改变单位向量的系数来调整p的模,从而满足条件二了,这个系数也是非常容易确定的。