刚体变换
即变换不改变长度、角度以及偏手性(不会让左右手坐标系颠倒)。
下面的平移变换、旋转变换即属于刚体变换
平移
从一个位置变到另一个位置可以用平移矩阵T来表示,这个矩阵将一个实体变换一个向量t = (tx, ty, tz).

如对于点P=(px,py,pz,1),经过平移变换后,即T(t)P=P'=(px + tx, py + ty, pz + tz, 1)
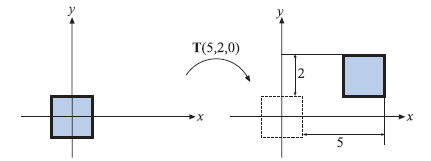
平移变换的逆矩阵与原来的平移量相同,但是方向相反
T-1 (t)=T(-t)

旋转
旋转变换将一个向量(位置或方向)绕给定轴旋转给定的角度。旋转变换矩阵通常用Rx(φ),Ry(φ),Rz(φ)来表示,即一个实体绕x,y及z轴分别旋转φ弧度
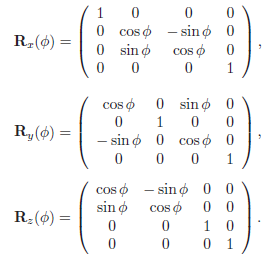
例子,将一个物体绕z轴以某个点p为中心点旋转φ弧度,那么我们首先将点p作为原点,即将物体平移到原点,如平移变换中所说,使用矩阵T(-p),然后再用旋转矩阵Rz(φ),最后在将物体平移回去到原先的原点。式子如下:
X = T(p)Rz(φ)T(-p)

缩放
缩放矩阵S(s)=S(sx,sy,sz)将一个实体以沿着x,y和z方向以sx,sy,sz的倍数缩放

如果sx=sy=sz,则叫均匀(uniform,or isotropic)缩放,否则就叫不均匀(nonuniform, or anisotropic)缩放。
如果sx,sy,sz中任意一个为负数,我们称矩阵为反射矩阵(reflection matrix,or mirror matrix)
剪切
剪切变换在游戏中可以扭曲整个场景来实现迷幻效果或者通过抖动产生模糊反射。
有6个剪切矩阵Hxy(s), Hxz(s),Hyx(s),Hyz(s),Hzx(s),Hzy(s),第一个下标用来表示哪个坐标会被改变,第二个下标表示做剪切的坐标。如Hxz(s)可以表示为
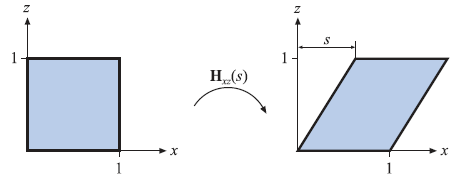
法线变换
不能直接用模型变换矩阵来变换Normal,比如使用某含有非一致性缩放(在x,y,z方向上进行不程度的拉伸)的变换矩阵来变换一球体,则可能得到如下列图示的结果:

左图为原始球体及其表面上的法向分布(2D投影后);中间为直接使用变换矩阵操作后的法向分布,但注意其明显与表面不垂直;右图为正确变换后的法向分布。
逆矩阵
逆矩阵在很多时候会用到,譬如,在坐标系统中改变后面和前面。
一般有三种方法计算逆矩阵:
1. 如果矩阵是单个变换或者是一系列有给定参数的简单变换,那么
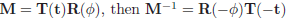
2. 如果矩阵是正交矩阵,那么 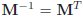
即逆矩阵就是转置矩阵
3. 如果没有任何特别之处,那么可以使用 adjoint method, Cramer's rule, LU decompostion,Gaussian elimination来计算逆矩阵