Preface
为了得到更好的纹理,很多人采用各种形式的柏林噪声(该命名来自于发明人 Ken Perlin)
柏林噪声是一种比较模糊的白噪声的东西:(引用书中一张图)

柏林噪声是用来生成一些看似杂乱无章其实有些变换规律的图形(更加贴近自然),比如海水、地形、雾等
当然这里面的原理涉及分形几何等相关的知识
例如,2D柏林噪声可以生成

以及一些网上的总结:
还有一些其他的图




是不是看起来自然多了
那么今天,我们就来领略一下随机技术带来的自然之美~
Chapter 4:Perlin Noise
柏林噪声有2个关键的特点:
第一,输入相同的3D点,总能返回相同的随机值
第二,简单快捷,使用一些hack的方法,达到快速近似的效果。
关于随机数:
许多人在他们的程序中使用“随机数产生器”,以使得物体的运动行为更加自然,或者用来生成纹理。随机数产生器在一些情况下很有用,比如用在模拟自然物体的地方,如地形,海水等。
自然物体通常是分形的,有各种各样的层次细节,比如山的轮廓,通过高度区分就有高山(mountain,高度变化大)、山丘(hill,高度变化适中)、巨石(高度变化小) 、石头(高度变化很小)等。另外,比如草地、海浪、跑动的蚂蚁、摇晃的树枝、风、大理石的花纹等等,这些都呈现出了或大或小的细节变化。Perlin噪声函数通过噪声函数来模拟这些自然景观。
要构造一个Perlin函数,首先需要一个噪声函数和一个插值函数。
我们第一步当然是构建一个Perlin的类
class Perlin { public: inline rtvar noise(const rtvec& p)const; inline static rtvar* randomvalue() { return _randomvalue; } inline static int* perm_x() { return _perm_x; } inline static int* perm_y() { return _perm_y; } inline static int* perm_z() { return _perm_z; } public: static rtvar* perlin_generate(); static int* perlin_generate_perm(); static void permute(int* p, int n);
private: static rtvar* _randomvalue; static int* _perm_x; static int* _perm_y; static int* _perm_z; };
我们来介绍一下,第一个public包含的是和该类相关的成员函数
第二个public是我们的随机数生成函数,它们按理说应该和此类无关,但是放在类外,担心污染命名空间,所以暂时列为静态函数成员,毕竟它们和Perlin类有很大关系,最后的时候,再把所有的功能性全局函数封装到3D泛型库里面
类数据成员:分别是Perlin随机函数生成的随机序列以及三个方向的辅助随机分量序列
我们如下设置这三个随机函数
rtvar * Perlin::perlin_generate() { rtvar* p = new rtvar[256]; for (int i = 0; i < 256; ++i) p[i] = lvgm::rand01(); return p; } int* Perlin::perlin_generate_perm() { int * p = new int[256]; for (int i = 0; i < 256; ++i) p[i] = i; permute(p, 256); return p; } void Perlin::permute(int * p, int n) { for (int i = n - 1; i > 0; --i) { int target = int(lvgm::rand01() * (i + 1)); stds swap(p[i], p[target]); } }
然后用它们初始化静态数据成员
rtvar* Perlin::_randomvalue = Perlin::perlin_generate(); int* Perlin::_perm_x = Perlin::perlin_generate_perm(); int* Perlin::_perm_y = Perlin::perlin_generate_perm(); int* Perlin::_perm_z = Perlin::perlin_generate_perm();
其中,总随机序列由第一种方法生成,序列中的每一个元素均为0~1的随机数
分量的随机序列由第二种方法生成,即,初始序列为1-255,之后遍历整个序列,当前位置和一个随机生成的位置进行交换,已达到序列随机化
随机函数讲完了,我们来看一下产生噪声值的函数

u,v,w是插值时候用的,目前暂时不用
参数p为空间某点的位置(未经归一化或单位化)
上面的函数也很好懂,就不细说了
我们暂时先不管插值函数,我们先用这个试一下效果
class noise_texture :public texture { public: noise_texture() { } virtual rtvec value(rtvar u, rtvar v, const rtvec& p)const override; private: Perlin _noise; }; rtvec noise_texture::value(rtvar u, rtvar v, const rtvec& p)const { return rtvec(1, 1, 1) * _noise.noise(p); }
就是把原来的噪声值腾个地方,转个手,没什么变化
然后主函数中

相机参数依然是:(以后默认是这个)

得到的效果是这样的:

其实还有个中间产品,之前把noise中的最后一行写成了
return _randomvalue[_perm_x[i] ^ _perm_y[i] ^ _perm_z[i]];
结果得到了下图(未做到完全随机)
感觉这个手误形成图也挺好看的
第一个图片看起来有点生硬粗糙,不是很光滑,所以,我们采用线性插值光滑一下
rtvar Perlin::trilinear_interp(rtvar c[2][2][2], rtvar u, rtvar v, rtvar w) { rtvar accumulate = 0; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) accumulate += (i * u + (1 - i)*(1 - u))* (j * v + (1 - j)*(1 - v))* (k * w + (1 - k)*(1 - w))* c[i][j][k]; return accumulate; }
我们把插值函数加入到noise函数中,当然你也可以尝试其他的插值函数
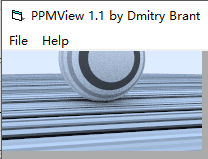
inline rtvar Perlin::noise(const rtvec& p)const { int i = floor(p.x()); int j = floor(p.y()); int k = floor(p.z()); rtvar u = p.x() - i; rtvar v = p.y() - j; rtvar w = p.z() - k; rtvar list[2][2][2]; for (int a = 0; a < 2; ++a) for (int b = 0; b < 2; ++b) for (int c = 0; c < 2; ++c) list[a][b][c] = _randomvalue[_perm_x[(i + a) & 255] ^ _perm_y[(j + b) & 255] ^ _perm_z[(k + c) & 255]]; return trilinear_interp(list, u, v, w); }
我们同时采用了随机生成函数和插值函数

我们还可以再尝试一下利用Hermit Cubic来进行舍入插值

它的频率依旧有点低,我们可以对参数施加一定的缩放比例,加速它的变化
也就是图像中的颜色更迭的太慢(I think)
class noise_texture :public texture { public: noise_texture() { } noise_texture(const rtvar scale); virtual rtvec value(rtvar u, rtvar v, const rtvec& p)const override; private: Perlin _noise; rtvar _scale; }; noise_texture::noise_texture(const rtvar scale) :_scale(scale) { } rtvec noise_texture::value(rtvar u, rtvar v, const rtvec& p)const { return rtvec(1, 1, 1) * _noise.noise(_scale * p); }
下面是scale 为 15 的图像

看起来密集多了,颜色变换频率也快了
下面是scale 为 1.5 的图像

显然,上面的图像格点还是很明晰的,可能是因为最小值和最大值总是精确地落在整数x / y / z上。 Ken Perlin采用了另一种技巧,将随机单位向量(而不仅仅是浮点数)放在格点上,并使用点积来移动格子的最小值和最大值。
所以,首先我们需要将随机浮点数更改为随机向量,试一试新的方法
下面是书上的代码,你运行之后打不开图像文件,因为里面是错的,我们边看边数说哪里错了
我们需要把数据成员_randomvalue改为static rtvec*
所以初始化语句也要改
rtvec * Perlin::_randomvalue = Perlin::perlin_generate(); int * Perlin::_perm_x = Perlin::perlin_generate_perm(); int * Perlin::_perm_y = Perlin::perlin_generate_perm(); int * Perlin::_perm_z = Perlin::perlin_generate_perm();
rtvec * Perlin::perlin_generate() { rtvec * p = new rtvec[256]; for (int i = 0; i < 256; ++i) p[i] = rtvec(-1 + 2 * lvgm::rand01(), -1 + 2 * lvgm::rand01(), -1 + 2 * lvgm::rand01()).ret_unitization(); return p; }
且看上面这段代码, -1 + 2*lvgm::rand01(),返回的区间为-1~1
inline rtvar Perlin::noise(const rtvec& p)const { int i = floor(p.x()); int j = floor(p.y()); int k = floor(p.z()); rtvar u = p.x() - i; rtvar v = p.y() - j; rtvar w = p.z() - k; rtvec list[2][2][2]; for (int a = 0; a < 2; ++a) for (int b = 0; b < 2; ++b) for (int c = 0; c < 2; ++c) { list[a][b][c] = _randomvalue[_perm_x[(i + a) & 255], _perm_y[(j + b) & 255], _perm_z[(k + c) & 255]]; #ifdef listtest if (list[a][b][c].x() < 0)stds cout << "list.x < 0 " << stds endl; if (list[a][b][c].y() < 0)stds cout << "list.y < 0 " << stds endl; if (list[a][b][c].z() < 0)stds cout << "list.z < 0 " << stds endl; #endif } return perlin_interp(list, u, v, w);
上述测试部分可能会输出信息,因为list中有负值,然后Perlin向量插值就可能会是负值
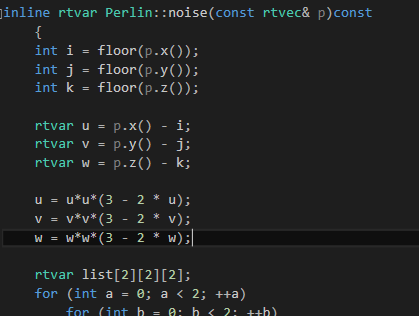
rtvar Perlin::perlin_interp(rtvec list[2][2][2], rtvar u, rtvar v, rtvar w) { rtvar uu = u*u*(3 - 2 * u); rtvar vv = v*v*(3 - 2 * v); rtvar ww = w*w*(3 - 2 * w); rtvar accumulate = 0; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) { rtvec weight(u - i, v - j, w - k); accumulate += (i*uu + (1 - i) * (1 - uu))* (j*vv + (1 - j) * (1 - vv))* (k*ww + (1 - k) * (1 - ww))* lvgm::dot(list[i][j][k], weight); #ifdef accumulatetest if (accumulate < 0)stds cout << "accumulate < 0 " << stds endl; #endif } return (accumulate); }
****************************** 为什么是“错”的 ***************************************
如果noise返回一个负值,那么
rtvec noise_texture::value(rtvar u, rtvar v, const rtvec& p)const { return rtvec(1., 1., 1.) *_noise.noise(p); }
它返回的就是一个负值
bool lambertian::scatter(const ray& rIn, const hitInfo& info, rtvec& attenuation, ray& scattered)const { rtvec target = info._p + info._n + lvgm::random_unit_sphere(); scattered = ray{ info._p, target - info._p }; attenuation = _albedo->value(0.,0.,info._p); return true; }
scatter传出去的attenuation就是负值
主函数中
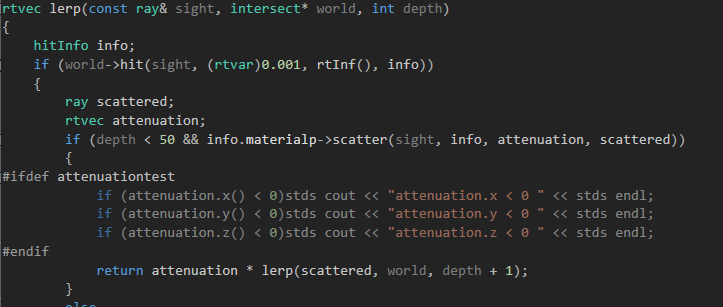
错误信息会输出成功,lerp函数返回含有负值的向量

gamma校正负值开根号为出现无穷
你的图像文件数据读取会报错!
****************************** 插曲结束 ***************************************
那么如果把随机生成函数改为
rtvec * Perlin::perlin_generate() { rtvec * p = new rtvec[256]; for (int i = 0; i < 256; ++i) p[i] = rtvec(abs(-1 + 2 * lvgm::rand01()), abs(-1 + 2 * lvgm::rand01()), abs(-1 + 2 * lvgm::rand01())).ret_unitization(); return p; }
还不行,因为noise会返回负值,那么我们把Perlin插值的返回值改为正值即可
rtvar Perlin::perlin_interp(rtvec list[2][2][2], rtvar u, rtvar v, rtvar w) { rtvar uu = u*u*(3 - 2 * u); rtvar vv = v*v*(3 - 2 * v); rtvar ww = w*w*(3 - 2 * w); rtvar accumulate = 0; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) { rtvec weight(u - i, v - j, w - k); accumulate += (i*uu + (1 - i) * (1 - uu))* (j*vv + (1 - j) * (1 - vv))* (k*ww + (1 - k) * (1 - ww))* lvgm::dot(list[i][j][k], weight); #ifdef accumulatetest if (accumulate < 0)stds cout << "accumulate < 0 " << stds endl; #endif } return abs(accumulate); //!!! }
那么我们的图片将是这个样子的
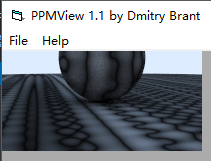
如果我们不改动随机数生成器,只保证noise函数最后的返回值为正值
那么也是上面那个图
改动间还得到了如下图:
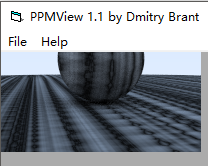
上面两个图是因为noise函数中list的值每次取得都和z有关,所以造成了上述线条现象

不小心重新抄写的时候将^写成了逗号,不过改为^也是错,因为不管怎么选择下标,该数组中的元素值始终都是-1~1
真正的解法是value取值的时候对noise的返回值做处理
下面是Perlin.hpp

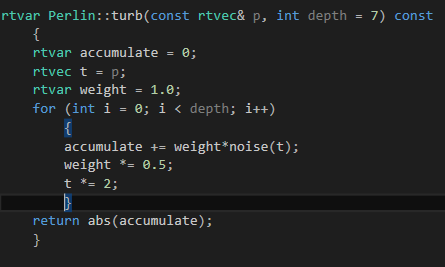
/// Perlin.hpp // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the Perlin-class for the ray-tracing project // from the 《ray tracing the next week》 // ----------------------------------------------------- #pragma once namespace rt { class Perlin { public: inline rtvar noise(const rtvec& p)const; inline rtvar turb(const rtvec& p, int depth) const; inline rtvec* randomvalue()const { return _randomvalue; } inline int* perm_x()const { return _perm_x; } inline int* perm_y()const { return _perm_y; } inline int* perm_z()const { return _perm_z; } public: static rtvec * perlin_generate(); static void permute(int * p, int n); static int * perlin_generate_perm(); static rtvar perlin_interp(rtvec list[2][2][2], rtvar u, rtvar v, rtvar w); private: static rtvec * _randomvalue; static int * _perm_x; static int * _perm_y; static int * _perm_z; }; rtvec * Perlin::_randomvalue = Perlin::perlin_generate(); int * Perlin::_perm_x = Perlin::perlin_generate_perm(); int * Perlin::_perm_y = Perlin::perlin_generate_perm(); int * Perlin::_perm_z = Perlin::perlin_generate_perm(); rtvec * Perlin::perlin_generate() { rtvec * p = new rtvec[256]; for (int i = 0; i < 256; ++i) p[i] = rtvec(-1 + 2 * lvgm::rand01(), -1 + 2 * lvgm::rand01(), -1 + 2 * lvgm::rand01()).ret_unitization(); return p; } int* Perlin::perlin_generate_perm() { int * p = new int[256]; for (int i = 0; i < 256; ++i) p[i] = i; permute(p, 256); return p; } void Perlin::permute(int* p, int n) { for (int i = n - 1; i; i--) { int tar = int(lvgm::rand01() * (i + 1)); stds swap(p[i], p[tar]); } } rtvar Perlin::turb(const rtvec& p, int depth = 7) const { rtvar accumulate = 0; rtvec t = p; rtvar weight = 1.0; for (int i = 0; i < depth; i++) { accumulate += weight*noise(t); weight *= 0.5; t *= 2; } return abs(accumulate); } inline rtvar Perlin::noise(const rtvec& p)const { int i = floor(p.x()); int j = floor(p.y()); int k = floor(p.z()); rtvar u = p.x() - i; rtvar v = p.y() - j; rtvar w = p.z() - k; rtvec list[2][2][2]; for (int a = 0; a < 2; ++a) for (int b = 0; b < 2; ++b) for (int c = 0; c < 2; ++c) { list[a][b][c] = _randomvalue[_perm_x[(i + a) & 255] ^ _perm_y[(j + b) & 255] ^ _perm_z[(k + c) & 255]]; #ifdef listtest if (list[a][b][c].x() < 0)stds cout << "list.x < 0 " << stds endl; if (list[a][b][c].y() < 0)stds cout << "list.y < 0 " << stds endl; if (list[a][b][c].z() < 0)stds cout << "list.z < 0 " << stds endl; #endif } return perlin_interp(list, u, v, w); } rtvar Perlin::perlin_interp(rtvec list[2][2][2], rtvar u, rtvar v, rtvar w) { #ifdef uvwtest if (u < 0)stds cout << "u < 0 " << stds endl; if (v < 0)stds cout << "v < 0 " << stds endl; if (w < 0)stds cout << "w < 0 " << stds endl; if (u > 1)stds cout << "u > 1 " << stds endl; if (v > 1)stds cout << "v > 1 " << stds endl; if (w > 1)stds cout << "w > 1 " << stds endl; #endif rtvar uu = u*u*(3 - 2 * u); rtvar vv = u*v*(3 - 2 * v); rtvar ww = u*w*(3 - 2 * w); rtvar accumulate = 0; for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j) for (int k = 0; k < 2; ++k) { rtvec weight(u - i, v - j, w - k); accumulate += (i*uu + (1 - i) * (1 - uu))* (j*vv + (1 - j) * (1 - vv))* (k*ww + (1 - k) * (1 - ww))* lvgm::dot(list[i][j][k], weight); #ifdef accumulatetest if (accumulate < 0)stds cout << "accumulate < 0 " << stds endl; #endif } return accumulate; } }
以及noise_texture.hpp中的value函数,如下:

方可解决noise中返回为负的情况,_scale 为 5 的时候做出的图如下:

同样,我们可以将光线追踪提高图片质量的惯用伎俩——采样,用在噪声值生成上面,即:使用具有多个相加频率的复合噪声。 这通常称为turbulence
用turb函数来代替noise函数,编者在turb返回的时候取了绝对值,而noise中的负值任由不管,不知为何。。

得到如下图:

既然,编者已经将turb返回值取了绝对值,我们大可试一下之前的value函数

_scale 为 5 时候

看着有点密集,和书上的不太像,把_scale调为3,得到如下图,看着差不多了
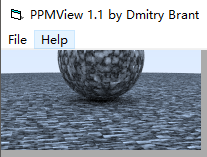
程序纹理的入门是大理石纹理, 基本思想是使颜色与正弦函数成比例,并使用turbulence来调整相位,能使条纹起伏

y = sin(wx + φ)
_scale就是w值,我实在调不出来书上的纹理

我把_scale的值调成6.3,结果如下:
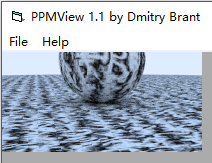
_scale 值越大,图像上的正弦曲线波动幅度越小
如果谁调整出来书上的_scale值了,请于下方评论区留言
我们不妨把value函数中的turb改为原来的noise

则得到下面这幅图

可以看到比较明显的格块状,所以turb还是好一点
今天就到这儿了,感谢您的阅读,生活愉快~
