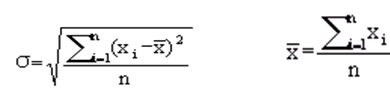https://www.lydsy.com/JudgeOnline/problem.php?id=2428
https://www.luogu.org/problemnew/show/P2503
已知N个正整数:A1、A2、……、An 。今要将它们分成M组,使得各组数据的数值和最平均,即各组的均方差最小。均方差公式如下
其中σ为均方差,
是各组数据和的平均值,xi为第i组数据的数值和。
我们做过很多类似这样的题,首先将均方差式子展开就会发现答案是小是大只和sigma(xi^2)有关。
所以我们可以dp……等等,貌似这个序列可以任取啊……dp好像做不了。
于是我们乱搞模拟退火,每次对这个序列随机交换两个元素,然后dp check一下ans是否能变小就行了。
dp方程太简单了我就懒得写了。
#include<cmath> #include<queue> #include<cstdio> #include<cctype> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> using namespace std; typedef long double dl; const int N=25; const dl T=3157; const dl eps=1e-15; const dl delta=0.998; inline int read(){ int X=0,w=0;char ch=0; while(!isdigit(ch)){w|=ch=='-';ch=getchar();} while(isdigit(ch))X=(X<<3)+(X<<1)+(ch^48),ch=getchar(); return w?-X:X; } int n,m,a[N],s[N],f[N][10]; dl sum,rms,t,ans=9e18; inline int sigma(int l,int r){ return (s[r]-s[l-1])*(s[r]-s[l-1]); } inline int suan(){ memset(f,127,sizeof(f)); for(int i=1;i<=n;i++){ s[i]=s[i-1]+a[i]; f[i][1]=sigma(1,i); for(int j=2;j<=min(i,m);j++){ for(int k=1;k<i;k++){ f[i][j]=min(f[i][j],f[k][j-1]+sigma(k+1,i)); } } } return f[n][m]; } void simulate_anneal(){ t=T; while(t>eps){ int i=rand()%n+1,j=rand()%n+1; swap(a[i],a[j]); dl nans=suan(); dl dans=nans-ans; if(nans<ans||rand()<exp(-dans/t)*RAND_MAX)ans=nans; else swap(a[i],a[j]); t*=delta; } } int main(){ srand(19260817); n=read();m=read(); for(int i=1;i<=n;i++)a[i]=read(),sum+=a[i]; simulate_anneal(); rms=sum/m; ans=sqrt((ans-rms*rms*m)/m); printf("%.2Lf ",ans); return 0; }
+++++++++++++++++++++++++++++++++++++++++++
+本文作者:luyouqi233。 +
+欢迎访问我的博客:http://www.cnblogs.com/luyouqi233/+
+++++++++++++++++++++++++++++++++++++++++++