中心投影变换解算 前后坐标

中心投影变换解算前后坐标

　　前言：文章的目的是为了通过三对 投影平面的点和三维空间中的点，解算出平面内其他点在三维空间中某个平面内的坐标。（这里只有对三维点的平面约束，才能解算出z；值得注意的是，三对点求解P3P问题往往会有多解（2个或者四个等），但是这个在本文中不影响，因为这里可以通过任一投影解来计算三维空间中平面内的坐标）

 

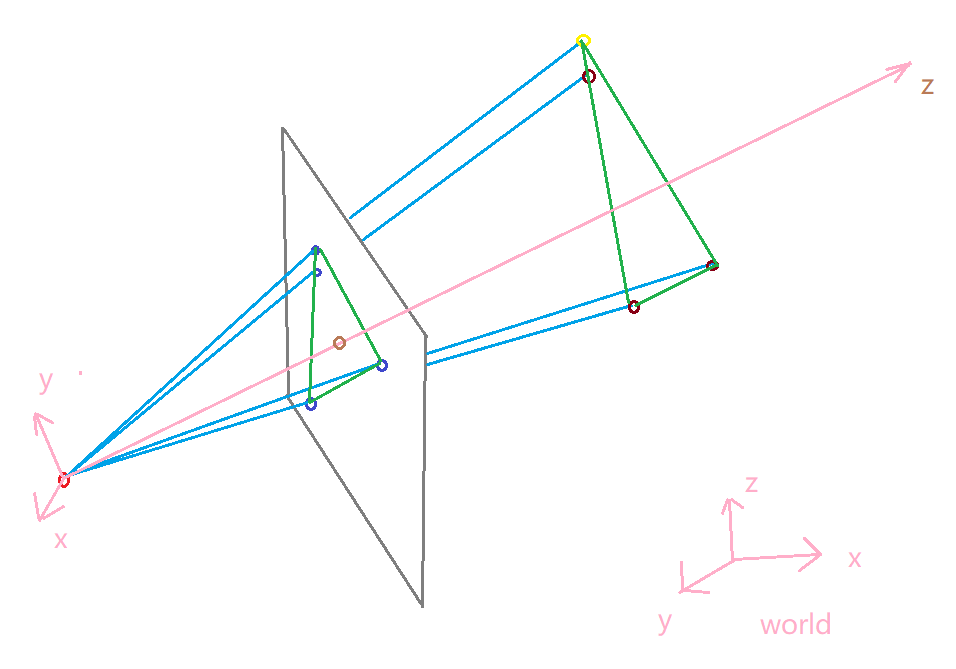
图1

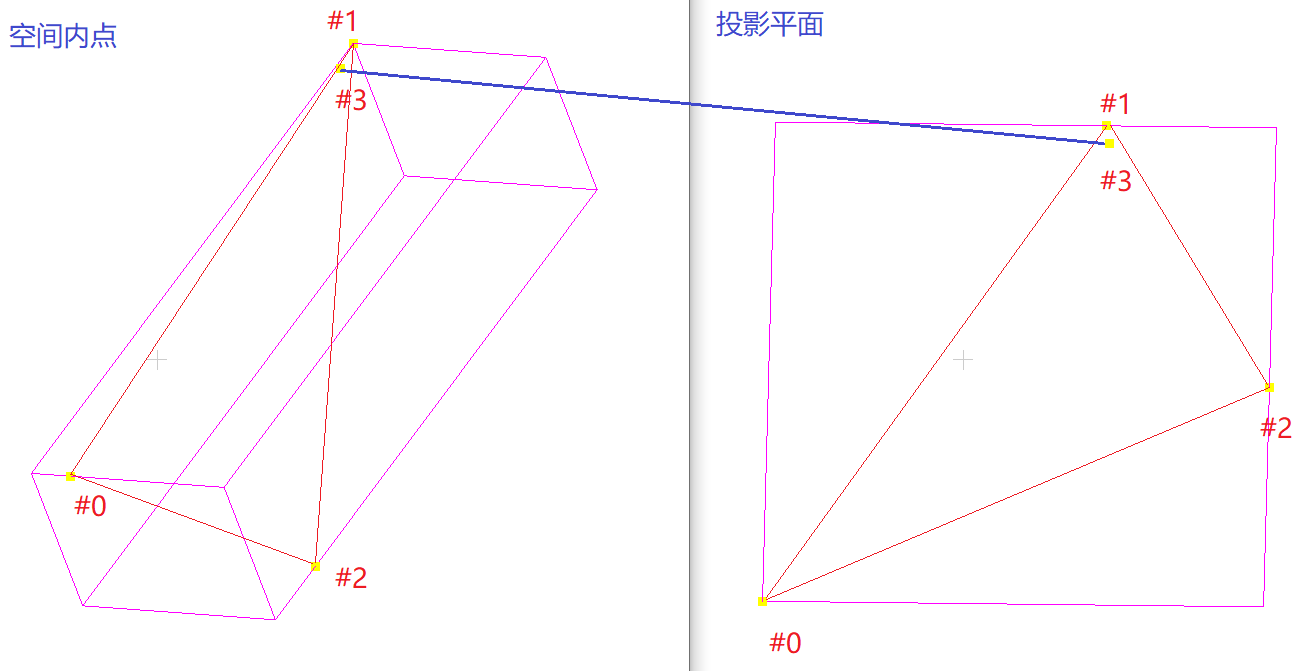
图2

 

//uvpoint caculate  mesh point 
int GTexture::uv2world(cv::Mat& rvec, cv::Mat& tvec, Plane& pl, PointT& pt2d, PointT& pt3d) {

    cv::Mat rotationMatrix = cv::Mat(3, 3, cv::DataType<double>::type);
    cv::Rodrigues(rvec, rotationMatrix);
    PointT uvpoint;
    uvpoint.x = pt2d.x;
    uvpoint.y = pt2d.y;
    uvpoint.z = 1.0;

    double z[3];  // coefficient of z
    double con[3];   // const num of z
    cv::Mat rotation_inv = rotationMatrix.inv();

    z[0] = rotation_inv.ptr<double>(0)[0] * uvpoint.x +
           rotation_inv.ptr<double>(0)[1] * uvpoint.y +
           rotation_inv.ptr<double>(0)[2] * uvpoint.z;

    z[1] = rotation_inv.ptr<double>(1)[0] * uvpoint.x +
           rotation_inv.ptr<double>(1)[1] * uvpoint.y +
           rotation_inv.ptr<double>(1)[2] * uvpoint.z;

    z[2] = rotation_inv.ptr<double>(2)[0] * uvpoint.x +
           rotation_inv.ptr<double>(2)[1] * uvpoint.y +
           rotation_inv.ptr<double>(2)[2] * uvpoint.z;

    con[0] = rotation_inv.ptr<double>(0)[0] * tvec.ptr<double>(0)[0]*(-1.0) +
        rotation_inv.ptr<double>(0)[1] * tvec.ptr<double>(0)[1] * (-1.0) +
        rotation_inv.ptr<double>(0)[2] * tvec.ptr<double>(0)[2] * (-1.0);

    con[1] = rotation_inv.ptr<double>(1)[0] * tvec.ptr<double>(0)[0] * (-1.0) +
        rotation_inv.ptr<double>(1)[1] * tvec.ptr<double>(0)[1] * (-1.0) +
        rotation_inv.ptr<double>(1)[2] * tvec.ptr<double>(0)[2] * (-1.0);

    con[2] = rotation_inv.ptr<double>(2)[0] * tvec.ptr<double>(0)[0] * (-1.0) +
        rotation_inv.ptr<double>(2)[1] * tvec.ptr<double>(0)[1] * (-1.0) +
        rotation_inv.ptr<double>(2)[2] * tvec.ptr<double>(0)[2] * (-1.0);

    //Plane pl;
    double temp = -1.0 * (con[0] * pl.A+ con[1] * pl.B + con[2] * pl.C + pl.D) / (z[0] * pl.A + z[1] * pl.B + z[2] * pl.C);

    pt3d.x = temp * z[0] + con[0];
    pt3d.y = temp * z[1] + con[1];
    pt3d.z = temp * z[2] + con[2];

    return 0;
}