BZOJ1502：[NOI2005]月下柠檬树——题解

https://www.lydsy.com/JudgeOnline/problem.php?id=1502

https://www.luogu.org/problemnew/show/P4207

李哲非常非常喜欢柠檬树，特别是在静静的夜晚，当天空中有一弯明月温柔地照亮地面上的景物时，他必会悠闲地坐在他亲手植下的那棵柠檬树旁，独自思索着人生的哲理。李哲是一个喜爱思考的孩子，当他看到在月光的照射下柠檬树投在地面上的影子是如此的清晰，马上想到了一个问题：树影的面积是多大呢？李哲知道，直接测量面积是很难的，他想用几何的方法算，因为他对这棵柠檬树的形状了解得非常清楚，而且想好了简化的方法。李哲将整棵柠檬树分成了n 层，由下向上依次将层编号为1,2,…,n。从第1到n-1 层，每层都是一个圆台型，第n 层(最上面一层)是圆锥型。对于圆台型，其上下底面都是水平的圆。对于相邻的两个圆台，上层的下底面和下层的上底面重合。第n 层(最上面一层)圆锥的底面就是第n-1 层圆台的上底面。所有的底面的圆心(包括树顶)处在同一条与地面垂直的直线上。李哲知道每一层的高度为h1,h2,…,hn，第1 层圆台的下底面距地面的高度为h0，以及每层的下底面的圆的半径r1,r2,…,rn。李哲用熟知的方法测出了月亮的光线与地面的夹角为alpha。

 

为了便于计算，假设月亮的光线是平行光，且地面是水平的，在计算时忽略树干所产生的影子。

李哲当然会算了，但是他希望你也来练练手。

参考：https://www.luogu.org/blog/ACdreamer/solution-p4207

超级细节之计算几何题。

面积的并选择用自适应辛普森求，我们只取x轴以上的部分，最后答案*2即可。

于是我们需要做到给定x求y，就需要求出这一坨投射的阴影的每个部分的函数（圆的部分可以用几何求y）。

于是需要求出圆的公切线的解析式。

首先对于高度h，投射后的长度为cota*h，圆的大小没有改变。

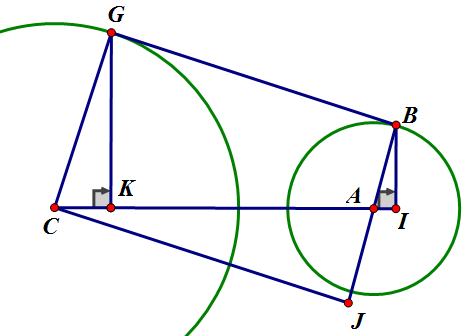
然后就是贴心的两张图了，根据这两张图，再结合你的初中几何知识，相信你一定能推出来的！

#include<cmath>
#include<queue>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef double dl;
const int N=510;
const dl eps=1e-8;
struct cir{
    dl x,r;
}p[N];
struct line{
    dl k,b,l,r;
}q[N];
int n;
dl alpha;
inline dl py(dl a,dl b){return sqrt(a*a-b*b);}
inline dl f(dl x){
    dl ans=0;
    for(int i=1;i<=n;i++){
        if(p[i].x-p[i].r<x&&x<p[i].x+p[i].r){
            ans=max(ans,py(p[i].r,x-p[i].x));
        }
    }
    for(int i=1;i<n;i++){
        if(q[i].l<=x&&x<=q[i].r){
            ans=max(ans,q[i].k*x+q[i].b);
        }
    }
    return ans;
}
inline dl simpson(dl l,dl r){
    dl mid=(l+r)/2;
    return (f(l)+4*f(mid)+f(r))*(r-l)/6;
}
inline dl asr(dl l,dl r,dl ans){
    dl mid=(l+r)/2;
    dl l1=simpson(l,mid),r1=simpson(mid,r);
    if(fabs(l1+r1-ans)<eps)return l1+r1;
    return asr(l,mid,l1)+asr(mid,r,r1);
}
inline int shadow(dl a){
    dl c=a*alpha;
    dl d=sqrt(a*a+c*c);
    return c*a/d;
}
inline void getl(int x,int y){
    if(fabs(p[x].r-p[y].r)<eps){
        q[x].l=p[x].x,q[x].r=p[y].x;
        q[x].k=0;q[x].b=p[x].r;
        return;
    }
    dl CA=p[y].x-p[x].x,AJ=fabs(p[x].r-p[y].r);
    dl CG=p[x].r,AB=p[y].r;
    dl CK=CG*AJ/CA,AI=AB*AJ/CA;
    if(p[x].r>p[y].r){
        q[x].l=p[x].x+CK;q[x].r=p[y].x+AI;
        dl x1=q[x].l,y1=py(CG,CK);
        dl x2=q[x].r,y2=py(AB,AI);
        q[x].k=(y1-y2)/(x1-x2);
        q[x].b=y1-q[x].k*x1;
    }else{
        q[x].l=p[x].x-CK;q[x].r=p[y].x-AI;
        dl x1=q[x].l,y1=py(CG,CK);
        dl x2=q[x].r,y2=py(AB,AI);
        q[x].k=(y1-y2)/(x1-x2);
        q[x].b=y1-q[x].k*x1;
    }
}
int main(){
    scanf("%d%lf",&n,&alpha);
    alpha=1.0/tan(alpha);
    for(int i=1;i<=n+1;i++){
        scanf("%lf",&p[i].x);
        p[i].x*=alpha;
        p[i].x+=p[i-1].x;
    }
    for(int i=1;i<=n;i++)scanf("%lf",&p[i].r);
    p[++n].r=0;
    for(int i=1;i<n;i++){
        getl(i,i+1);
    }
    dl l=p[1].x-p[1].r,r=p[n].x;
    for(int i=1;i<=n;i++){
    r=max(r,(p[i].x+p[i].r));
    l=min(l,(p[i].x-p[i].r));
    }
    printf("%.2lf
",2*asr(l,r,simpson(l,r)));
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

 +本文作者：luyouqi233。 　　　　　　　　　　　　　　+

 +欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++