DBoW2库是University of Zaragoza里的Lopez等人开发的开源软件库。
由于在SLAM回环检测上的优异表现(特别是ORB-SLAM2),DBoW2库受到了广大SLAM爱好者的关注。本文希望通过深入解析DBoW2库及相关的DLoopDetector库,为读者后续使用这两个库提供参考。
git地址:
DBoW2
DLoopDetector
论文:Bags of Binary Words for Fast Place Recognition in Image Sequences
DBoW2库介绍
词袋模型
BoW(Bag of Words,词袋模型),是自然语言处理领域经常使用的一个概念。以文本为例,一篇文章可能有一万个词,其中可能只有500个不同的单词,每个词出现的次数各不相同。词袋就像一个个袋子,每个袋子里装着同样的词。这构成了一种文本的表示方式。这种表示方式不考虑文法以及词的顺序。
在计算机视觉领域,图像通常以特征点及其特征描述来表达。如果把特征描述看做单词,那么就能构建出相应的词袋模型。这就是本文介绍的DBoW2库所做的工作。利用DBoW2库,图像可以方便地转化为一个低维的向量表示。比较两个图像的相似度也就转化为比较两个向量的相似度。它本质上是一个信息压缩的过程。
视觉词典
词袋模型利用视觉词典(vocabulary)来把图像转化为向量。视觉词典有多种组织方式,对应于不同的搜索复杂度。DBoW2库采用树状结构存储词袋,搜索复杂度一般在log(N),有点像决策树。
词典的生成过程如下图。
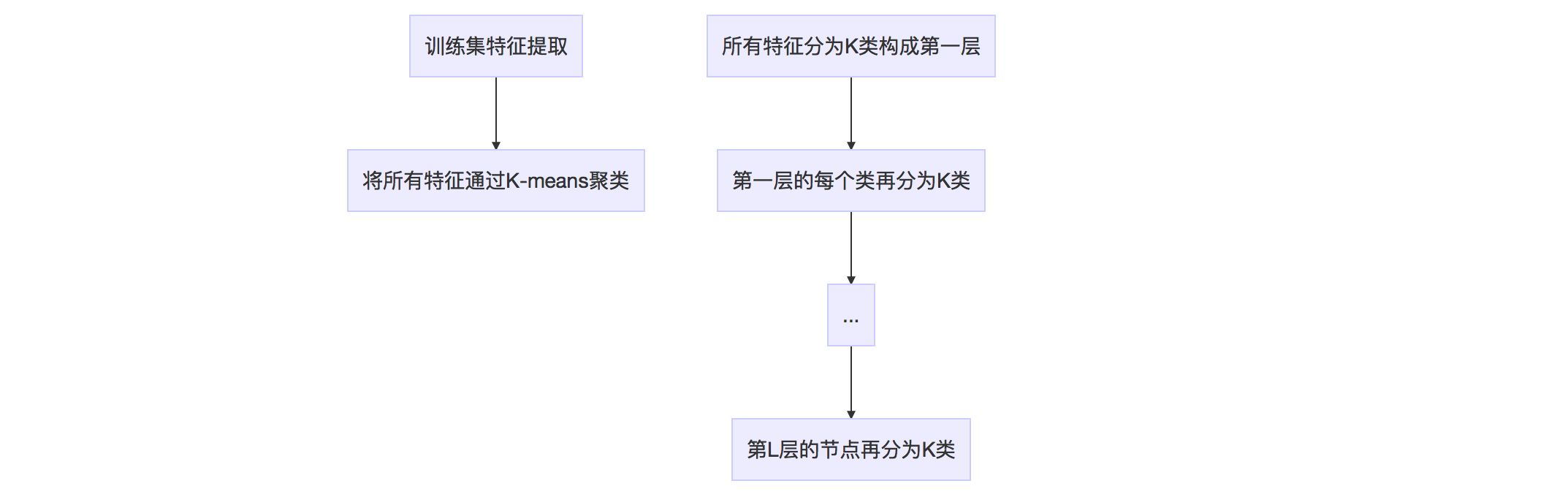
这棵树里面总共有(1+K+cdots+K^L=(k^{L+1}-1)/(K-1))个节点。所有叶节点在(L)层形成(W=K^L)类,每一类用该类中所有特征的平均特征(meanValue)作为代表,称为单词(word)。每个叶节点被赋予一个权重。作者提供了TF、IDF、BINARY、TF-IDF等权重作为备选,默认为TF-IDF。
TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的频率TF高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。TF-IDF实际上是TF * IDF,TF代表词频(Term Frequency),表示词条在文档d中出现的频率。IDF代表逆向文件频率(Inverse Document Frequency)。如果包含词条t的文档越少,IDF越大,表明词条t具有很好的类别区分能力。(来自百度百科)
第k个叶节点(单词)的TF和IDF分别定义为
视觉词典可以通过离线训练大量数据得到。训练中只计算和保存单词的IDF值,即单词在众多图像中的区分度。TF则是从实际图像中计算得到各个单词的频率。单词的TF越高,说明单词在这幅图像中出现的越多;单词的IDF越高,说明单词本身具有高区分度。二者结合起来,即可得到这幅图像的BoW描述。
假设训练集有10万幅图像,每幅图像提取出200个特征,总共有两千万个特征。如果我们取K=10,L=6,那么词典总共有十万个节点,压缩了200倍。K和L需要根据场景的丰富程度和特征的区分度选取。
在DBoW2库中,如果特征描述是ORB特征,那就训练得到ORB词典;如果是SIFT特征,那就训练得到SIFT词典。DBoW2库利用一个大的图像数据库,离线训练好了ORB库和SIFT库,供大家使用。因此,在使用DBoW2库时,首先需要载入一个离线视觉词典。
ORB-SLAM2中,那个100多兆的文件就是ORB词典。
注意ORB特征和SIFT特征对于meanValue()和distance()的定义有所不同。
代码解析
生成词典的函数位于TemplatedVocabulary.h,具体实现为
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor,F>::create(
const std::vector<std::vector<TDescriptor> > &training_features, // 图像特征集合
int k, // 每层的类的个数
int L, // 树的层数
WeightingType weighting, // 权重的类型,默认为TF-IDF
ScoringType scoring) // 得分的类型,默认为L1-norm
{
m_nodes.clear();
m_words.clear();
// 节点数 = Sum_{i=0..L} ( k^i )
int expected_nodes = (int)((pow((double)m_k, (double)m_L + 1) - 1)/(m_k - 1));
m_nodes.reserve(expected_nodes); // avoid allocations when creating the tree
// 将所有特征描述集合到一个vector
std::vector<pDescriptor> features;
getFeatures(training_features, features);
// 生成根节点
m_nodes.push_back(Node(0)); // root
// k-means++(内有递归)
HKmeansStep(0, features, 1);
// 建立一个只有叶节点的序列m_words
createWords();
// 为每个叶节点生成权重,此处计算IDF部分,如果不用IDF,则设为1
setNodeWeights(training_features);
}
k-means++过程
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::HKmeansStep
(
NodeId parent_id, // 父节点id
const std::vector<pDescriptor> &descriptors, // 该父节点对应的特征描述集合
int current_level // 当前层数
)
{
if (descriptors.empty()) return;
// 用来存储子节点的特征描述 features associated to each cluster
std::vector<TDescriptor> clusters;
// 用来存储每个子节点对应的特征描述在descriptors向量中的id
std::vector<std::vector<unsigned int> > groups; // groups[i] = [j1, j2, ...]
// j1, j2, ... indices of descriptors associated to cluster i
clusters.reserve(m_k);
groups.reserve(m_k);
// 如果特征描述个数小于m_k,直接分类
if ((int)descriptors.size() <= m_k) {
// trivial case: one cluster per feature
groups.resize(descriptors.size());
for (unsigned int i = 0; i < descriptors.size(); i++) {
groups[i].push_back(i);
clusters.push_back(*descriptors[i]);
}
} else {
// k-means分类
bool first_time = true;
bool goon = true;
// 用于检查迭代过程中前后两次分类结果是否一致,如一致,分类结束
std::vector<int> last_association, current_association;
// 迭代过程
while (goon) {
// 1. 分类
if (first_time) {
// 第一次,初始化分类
initiateClusters(descriptors, clusters);
} else {
// 计算每一类的meanValue
for (unsigned int c = 0; c < clusters.size(); ++c) {
std::vector<pDescriptor> cluster_descriptors;
cluster_descriptors.reserve(groups[c].size());
// 利用group,读取每一类对应的id
std::vector<unsigned int>::const_iterator vit;
for (vit = groups[c].begin(); vit != groups[c].end(); ++vit) {
cluster_descriptors.push_back(descriptors[*vit]);
}
// 计算meanValue
F::meanValue(cluster_descriptors, clusters[c]);
}
} // if(!first_time)
// 2. 利用1计算的中心重新分类
groups.clear();
groups.resize(clusters.size(), std::vector<unsigned int>());
current_association.resize(descriptors.size());
typename std::vector<pDescriptor>::const_iterator fit;
// 对每一个特征,计算它与K个中心特征的距离,标记距离最小的中心特征的id
for (fit = descriptors.begin(); fit != descriptors.end(); ++fit) { //, ++d)
double best_dist = F::distance(*(*fit), clusters[0]);
unsigned int icluster = 0;
for (unsigned int c = 1; c < clusters.size(); ++c) {
double dist = F::distance(*(*fit), clusters[c]);
if (dist < best_dist) {
best_dist = dist;
icluster = c;
}
}
// 记录分类信息
groups[icluster].push_back(fit - descriptors.begin());
current_association[ fit - descriptors.begin() ] = icluster;
}
// kmeans++ ensures all the clusters has any feature associated with them
// 3. 检查前后两次分类结果是否一致,如一致,分类结束
if (first_time) {
first_time = false;
} else {
goon = false;
for (unsigned int i = 0; i < current_association.size(); i++) {
if (current_association[i] != last_association[i]) {
goon = true;
break;
}
}
}
// 如果不一致,存储本次分类信息
if (goon) {
// copy last feature-cluster association
last_association = current_association;
}
} // while(goon)
} // if must run kmeans
// 生成本层的节点,其特征描述为每一类的meanValue
for (unsigned int i = 0; i < clusters.size(); ++i) {
NodeId id = m_nodes.size();
m_nodes.push_back(Node(id));
m_nodes.back().descriptor = clusters[i];
m_nodes.back().parent = parent_id;
m_nodes[parent_id].children.push_back(id);
}
// 如果没有达到L层,继续分类
if (current_level < m_L) {
// iterate again with the resulting clusters
const std::vector<NodeId> &children_ids = m_nodes[parent_id].children;
for (unsigned int i = 0; i < clusters.size(); ++i) {
// 当前层的节点id
NodeId id = children_ids[i];
std::vector<pDescriptor> child_features;
child_features.reserve(groups[i].size());
std::vector<unsigned int>::const_iterator vit;
// 该id对应的特征描述集合
for (vit = groups[i].begin(); vit != groups[i].end(); ++vit) {
child_features.push_back(descriptors[*vit]);
}
// 进入下一层,继续分类
if (child_features.size() > 1) {
HKmeansStep(id, child_features, current_level + 1);
}
}
}
}
可以看出,词典树的所有节点是按照层数来排列的。
图像识别
离线生成视觉词典以后,我们就能在线进行图像识别或者场景识别。实际应用中分为两步进行。
第一步:为图像生成一个表征向量(v_{1 imes W})。图像中的每个特征都在词典中搜索其最近邻的叶节点。所有叶节点上的权重集合构成了BoW向量(v)。
第二步:根据BoW向量,计算当前图像和其它图像之间的距离(s(v_1,v_2))
有了距离定义,即可根据距离大小选取合适的备选图像。
正向索引与反向索引
在视觉词典之上,作者还加入了Database的概念,并引入了正向索引(direct index)和反向索引(inverse index)的概念。这部分代码位于TemplatedDatabase.h中。
反向索引
作者用反向索引记录每个叶节点对应的图像编号。当识别图像时,根据反向索引选出有着公共叶节点的备选图像并计算得分,而不需要计算与所有图像的得分。反向索引定义为
// InvertedFile为所有叶节点反向索引的集合
// 每个叶节点(word)有一个反向索引,定义为IFRow
typedef std::vector<IFRow> InvertedFile;
// InvertedFile[word_id] --> inverted file of that word
// IFRow定义list,为一系列图像编号的集合
// IFRows根据图像编号的升序排列
typedef std::list<IFPair> IFRow;
struct IFPair
{
// Entry id,图像编号
EntryId entry_id;
// Word weight in this entry,叶节点权重
WordValue word_weight;
}
其中IFPair储存图像编号和叶节点的权重(此处保存权重可方便得分s的计算)。
正向索引
当两幅图像进行特征匹配时,如果极线约束未知,那么只有暴力匹配,复杂度为(O(N^2)),或者先为特征生成k-d树再利用k-d树匹配,复杂度为(O(Nlog N))。作者提供了一种正向索引用于加速特征匹配。正向索引需要指定词典树中的层数,比如第m层。每幅图像对应一个正向索引,储存该图像生成BoW向量时曾经到达过的第m层上节点的编号,以及路过这个节点的那些特征的编号。正向索引的具体定义为
// DirectFile为所有图像正向索引的集合
// 每个图像有一个FeatureVector,
// 每个FeaturVector定义为std::map,map的元素为<node_id, std::vector<feature_id>>
typedef std::vector<FeatureVector> DirectFile;
// DirectFile[entry_id] --> [ node_id, vector<feature_id> ]
FeatureVector通过下面介绍的transform()函数得到。
假设两幅图像为A和B,下图说明如何利用正向索引来加速特征匹配的计算。
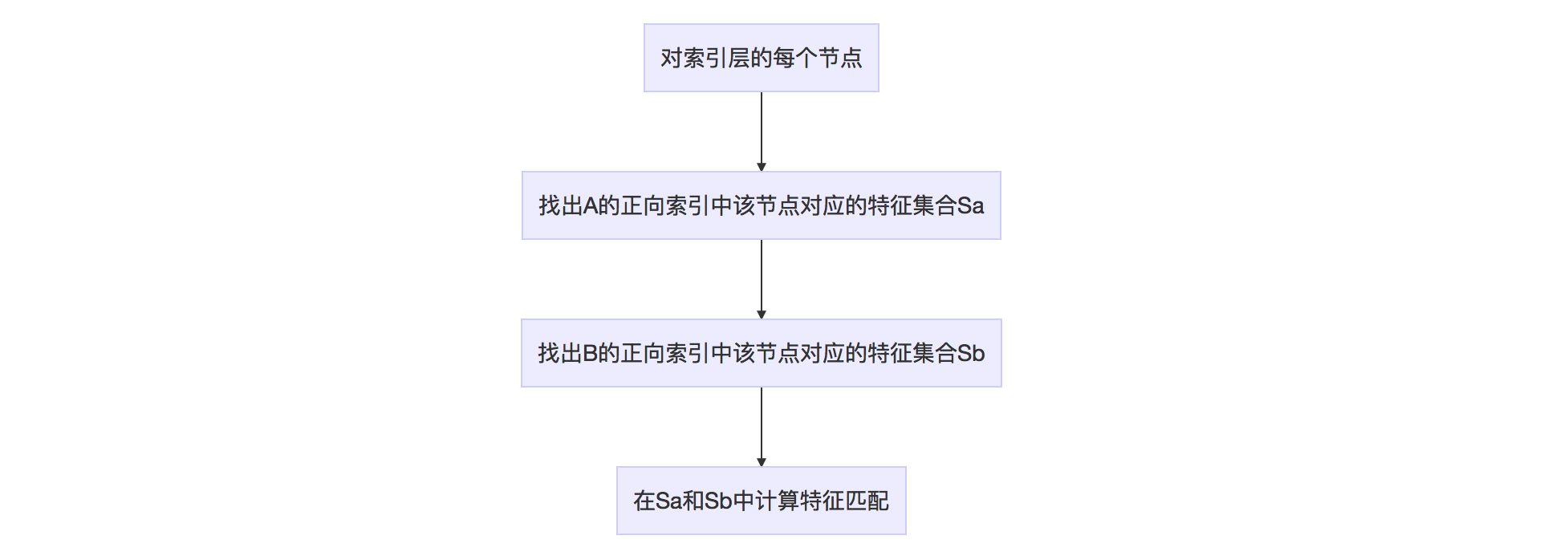
当然上述算法也可通过循环A或者B的正向索引来做。
这种加速特征匹配的方法在ORB-SLAM2中被大量使用。注意到,正向索引的层数如果选择第0层(根节点),那么时间复杂度和暴力搜索一样。如果是叶节点层,则搜索范围有可能太小,错失正确的特征点匹配。作者一般选择第二层或者第三层作为父节点(L=6)。正向索引的复杂度约为(O(N^2/K^m))。
代码解析
图像转化为BoW向量(包含正向索引)
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::transform
(
const std::vector<TDescriptor> &features, // 图像特征集合
BowVector &v, // bow向量,std::map<leaf_node_id, weight>
FeatureVector &fv, // 正向索引向量,std::map<direct_index_node_id, feature_id>
int levelsup // 正向索引的层数=L-levelsup
) const
{
// ignore some unimportant code here
// whether a vector must be normalized before scoring according
// to the scoring scheme
LNorm norm;
bool must = m_scoring_object->mustNormalize(norm);
typename std::vector<TDescriptor>::const_iterator fit;
// 依据权重类型,bow向量加入权重的方式有所不同
if (m_weighting == TF || m_weighting == TF_IDF) {
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为TF-IDF,w为IDF。如为TF,w为1
transform(*fit, id, w, &nid, levelsup);
// 加入权重
if (w > 0) { // not stopped
// 累积该叶节点的idf权重,v(id).weight += w
// 最后v(id).weight实际上等于M*idf,M为插入该叶节点的特征描述的个数
v.addWeight(id, w);
// 插入<node_id, feature_id>
fv.addFeature(nid, i_feature);
}
}
if (!v.empty() && !must) {
// unnecessary when normalizing
const double nd = v.size();
// 只有SCORING_CLASS=DotProductScoring时
for (BowVector::iterator vit = v.begin(); vit != v.end(); vit++)
vit->second /= nd;
}
} else { // IDF || BINARY
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为IDF,w为IDF。如为BINARY,w为1
transform(*fit, id, w, &nid, levelsup);
if (w > 0) { // not stopped
// 插入该叶节点的权重,v.insert(id,w)
v.addIfNotExist(id, w);
// 插入<node_id, feature_id>
fv.addFeature(nid, i_feature);
}
}
} // if m_weighting == ...
// 归一化bow向量,v=v/|v|
// 因为要归一化,所以之前计算的TF-IDF并没有除以TF的分母(特征的总数,对于bow向量中的所有项都相等)
if (must) v.normalize(norm);
}
单个图像特征寻找叶节点
template<class TDescriptor, class F>
void TemplatedVocabulary<TDescriptor, F>::transform
(
const TDescriptor &feature, // 当前带插入的特征描述
WordId &word_id, // 待取出的叶节点id(叶节点序列中的id,非树中的id)
WordValue &weight, // 待取出的权重
NodeId *nid, // 该特征描述对应的正向索引(树中某一层的父节点id)
int levelsup // 正向索引在第(L-levelsup)层上
) const
{
// 将当前特征描述插入词典树的叶节点层
std::vector<NodeId> nodes;
typename std::vector<NodeId>::const_iterator nit;
// 如果nid不为空,则nid储存该特征在第(L-levelsup)层上的父节点
// 用于正向指标
const int nid_level = m_L - levelsup;
if (nid_level <= 0 && nid != NULL) *nid = 0; // root
NodeId final_id = 0; // root
int current_level = 0;
// 逐层插入,直到叶节点层
do {
++current_level;
nodes = m_nodes[final_id].children;
final_id = nodes[0];
// 计算该特征与本层节点的距离,选取距离最小的节点
double best_d = F::distance(feature, m_nodes[final_id].descriptor);
for (nit = nodes.begin() + 1; nit != nodes.end(); ++nit) {
NodeId id = *nit;
double d = F::distance(feature, m_nodes[id].descriptor);
if (d < best_d) {
best_d = d;
final_id = id;
}
}
// 存储正向索引nid
if (nid != NULL && current_level == nid_level)
*nid = final_id;
} while ( !m_nodes[final_id].isLeaf() );
// 取出叶节点对应的word id(所有叶节点集合内的编号)和权重
word_id = m_nodes[final_id].word_id;
weight = m_nodes[final_id].weight;
}
权重更新过程
// 每幅图像有一个BoWVector
// TF-IDF或者TF采用这个函数
// 累积节点权重,bow向量是一个按WordId排序的有序序列
void BowVector::addWeight(WordId id, WordValue v)
{
// 找到第一个大于等于id的节点
BowVector::iterator vit = this->lower_bound(id);
// 找到了输入id对应的节点
// 权重+=v
if(vit != this->end() && !(this->key_comp()(id, vit->first)))
{
vit->second += v;
}
// 没有找到输入id,插入<id,v>
// vit==end()(id比现有WordId都大)
// 或者vit的id不等于输入的id
else
{
this->insert(vit, BowVector::value_type(id, v));
}
}
// IDF或者BINARY采用这个函数
// 当id不存在时,插入<id,v>
// 因为不考虑词频,所以每个叶节点只需要插入第一个到达此节点的权重值
void BowVector::addIfNotExist(WordId id, WordValue v)
{
BowVector::iterator vit = this->lower_bound(id);
if(vit == this->end() || (this->key_comp()(id, vit->first)))
{
this->insert(vit, BowVector::value_type(id, v));
}
}
FeatureVector更新过程
// 储存所有到达过某个node_id的feature_id(正向索引)
// 每幅图像有一个FeatureVector
void FeatureVector::addFeature(NodeId id, unsigned int i_feature)
{
// 找到第一个key大于等于node_id的项
FeatureVector::iterator vit = this->lower_bound(id);
// 如果key==node_id,push_back
if(vit != this->end() && vit->first == id)
{
vit->second.push_back(i_feature);
}
// 如果id还没有出现,插入<node_id,feature_id>
else
{
vit = this->insert(vit, FeatureVector::value_type(id,
std::vector<unsigned int>() ));
vit->second.push_back(i_feature);
}
}
DLoopDetector库介绍
在SLAM中,追踪(Tracking)得到的位姿通常都是有误差的。随着路径的不断延伸,前面帧的误差会一直传递到后面去,导致后续帧的姿态估计的误差越来越大。就好比一个人走在陌生的城市里,可能一开始还能分清东南西北,但随着在小街小巷转来转去,大概率已经无法定位自身的准确位置了。通过认真辨识周边环境,他可以建立起局部的地图信息(局部优化)。再回忆以前走过的路径,他可以纠正一些以前的地图信息(全局优化)。然而他还是不能确定自己在城市的精确方位。直到他看到了一个之前路过的地方,就会恍然大悟,“噢!原来我回到了这个地方”。此时,将这个信息传递回整个地图,配合全局优化,就可以很好地修正当前的地图信息。回环检测就是想办法找到以前经过的地方。
回环检测已经成为现代SLAM框架中非常重要的一环,特别是在大尺度地图构建上。回环检测如果从图像出发,就是比较两个图像的相似度。这就可以利用上面介绍DBoW2库来实现快速选取备选的回环图像。这就是DLoopDetector库的工作。
ORB-SLAM2中,作者利用DBoW2库,按照自己的标准选取回环图像,并没有用DLoopDetector库。具体可以参考作者文章和代码。
DLoopDetector库默认只输出一幅回环图像。如果需要多幅图像备选,自己修改一下程序即可。
为了鲁棒地选取回环图像,DLoopDetector库采用了如下准则。
归一化
根据前面的定义,两个BoW向量之间的得分定义为
因此,对于(t)时刻的图像,可以找到一系列图像和它有较高的得分,记为({t_j})。作者注意到,尽管(v)已经归一化,(s)还是会受到不同图像的特征分布的影响。作者进一步将得分归一化为
其中(s(v_t,v_{t-delta t}))为(t)时刻图像与(t-delta t)时刻图像的得分。当相机旋转很快时,分母会偏小,(eta)会偏大,因此还要规定一个最小的(s(v_t,v_{t-delta t})),默认值为0.005。另外,(eta)也需要达到一个最小值,默认值为0.3。
ORB-SLAM2用另外一种思路做了归一化。
最后,选取(eta)最大的若干幅图像,作为回环的备选图像。
分组
计算得分时,相邻两幅备选图像与当前图像的得分会很接近。为了选取更具代表性的图像,作者根据图像id(即时间顺序)对备选图像进行分组,计算和比较组间的得分,从而避免在小时间段内重复选取。定义一组(island)的得分为
下面给出一个简单的分组示意图。

当一个真正的回环出现时,回环附近的图像与当前图像的相似度都会比较高,因此计算累积得分能更好地区分出回环图像。
最后,选取得分最高的分组(V_{T'})。
时间一致性
找到最好的分组后,还要检查在一定时间内回环是否稳定存在。假设(t)时刻出现一个真正的回环,那么在接下来的一定时间内,回环应当是稳定存在的。因此,回环应该在时间上具有一致性。具体而言,(v_{t+kdelta t})时刻应该也检测出一个回环(V_{T'_k}),并且和(V_{T'})很接近(指组内的图像序列编号),(k=1,cdots,K)。如果回环在(K)个时刻都满足一致性,那么认为这是一个好的回环检测。默认参数(K=3)。
几何一致性
选定了回环图像后,作者还检查了两幅图像之间的几何一致性。通过计算两幅图像之间的基本矩阵(fundamental matrix),判断其内点数是否足够(作者选择的阈值是12)。如果不够,说明两幅图像之间的特征匹配并不可靠,予以拒绝。作者利用之前介绍的正向索引来加速特征匹配的计算。作者也提供了直接配对和k-d tree配对的算法。
代码分析
这里就不逐行分析代码了,介绍一下DLoopDetector里面的参数设置。代码位于TemplatedLoopDetector.h。
template <class TDescriptor, class F>
void TemplatedLoopDetector<TDescriptor,F>::Parameters::set(float f)
{
/// 计算得分的参数
// 回环的图片id应当小于当前id-dislocal
dislocal = 20 * f;
// 从data base中选出来的最大备选图像数量
max_db_results = 50 * f;
// s(v_t,v_{t-delta t})的最小值
min_nss_factor = 0.005;
// alpha:eta的最小值,default=0.3
/// 分组的参数
// 组内最少的图像数量
min_matches_per_group = f; //
// 两组之间最小的图像编号差,见示意图中的gap
max_intragroup_gap = 3 * f; //
/// 回环检测找到备选分组时,进行时间一致性检查的参数
// 前后两个时刻最佳备选分组之间的时间间隔应当比较小
max_distance_between_groups = 3 * f; //
// 当前图像id与上次一致性检查时的图像id的最大距离
// 前后两次检查之间的时间间隔应当较小
max_distance_between_queries = 2 * f;
// k: 最小entry的数目,default=3
// RANSAC 计算F矩阵的参数
min_Fpoints = 12; //
max_ransac_iterations = 500; //
ransac_probability = 0.99; //
max_reprojection_error = 2.0; //
// isGeometricallyConsistent_Flann中用到的参数
max_neighbor_ratio = 0.6; //
}
分析
基于DBoW2的方法有一些非常好的优势
- 速度快
- 场景识别的速度很快。小尺寸的图像可以在毫秒级别完成。
- 很多VSLAM本身就要计算特征点和特征描述,因此使用BoW方法不需要太多额外的计算时间。
- 利用词典可以加速特征匹配,特别是在大尺度场景上。
- 扩展性好
- 库本身并没有限制特征的类型,不局限于图像特征,只需要定义好distance()的计算方法。
- 可以用自定义的特征训练视觉词典。
- 使用方便
- 词典可以离线训练。作者提供了通过大量数据训练出来的BRIEF和SIFT的词典。
- 依赖性少
- 基本上只依赖于OpenCV和boost库(BRIEF需要boost::dynamic_bitset),非常轻量级。
当然它也有自己的劣势
- 作者提供的词典基于非常丰富的场景,因此占用空间大,加载速度慢。
- DBoW2中只考虑图像中的特征描述,丢失了特征的几何约束。
一些comments
- 如果应用本身不需要计算特征,那要考虑额外的计算时间。比如直接法。
- 推荐像ORB-SLAM2一样,利用DBoW2选出若干幅备选图像,后续通过其它方法验证。
- ORB-SLAM2利用Sim3优化来验证回环。
- RGBD-SLAM可利用点云匹配或者BA去验证回环。
- 如果场景特征很少,或者重复的特征太多,效果可能不佳。
- 现在有研究者基于深度学习来识别重复场景,也是非常好的思路,准确率更高。
SLAM中的应用
可参考ORB-SLAM2在重定位、特征匹配和回环检测中的应用。想强调的是,不要局限于作者提供的特征,结合使用场景,尝试自定义特征和训练词典。