最近看了些逻辑斯蒂方程的内容，其初始应用于生态学中的物种数量的预测，延伸到人口限制增长，信息传播，商品的销售预测问题等，此外，逻辑斯蒂方程还是非线性科学混沌学的一个著名的映射，是混沌的入口。
逻辑斯蒂方程的应用
1．人口限制增长问题
人口的增长不是呈指数型增长的，这是由于环境的限制、有限的资源和人为的影响，最终人口的增长将减慢下来。实际上，人口增长规律满足逻辑斯蒂方程。
2. 信息传播问题
所谓信息传播可以是一则新闻，一条谣言或市场上某种新商品有关的知识,在初期，知道这一信息的人很少，但是随时间的推移，知道的人越来越多，到一定时间，社会上大部分人都知道了这一信息．这里的数量关系可以用逻辑斯蒂方程来描述。若以t表示从信息产生算起的时间，P表示已知信息的人口比例，则逻辑斯蒂方程变为：
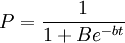...................(3)
例如,当某种商品调价的通知下达时，有10％的市民听到这一通知，2小时以后，25％的市民知道了这一信息，由逻辑斯蒂方程可算出有75％的市民了解这一情况所需要的时间。
在方程(3)中，由t=0时，P=10％可得 B＝9;再由t=2时，P=25％可得,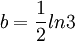
。
当P=75％时，有:
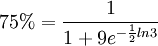
解得t=6，即6小时后，全市有75％的人了解这一通知。
3.商品销售预测问题
例如，某种商品的销售，开始时，知道的人很少，销售量也很小。当这种商品信息传播出去后，销售量大量增加，到接近饱和时销售量增加极为缓慢。比如，这种商品饱和量估计a=500(百万件)，大约5年可达饱和，常数b经测定为b=lnl0，B=100。下面我们来预测一下第3年末的销售量是多少。
由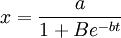
,有:
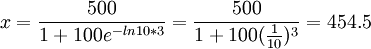(百万件)
所以第三年末的市场销售量大约为454.5百万件，这样可以做到有计划地生产。
逻辑斯蒂方程的应用比较广泛。如果问题的基本数量特征是：在时间t很小时，呈指数型增长，而当t增大时，增长速度就下降，且越来越接近于一个确定的值，这类问题可以用逻辑斯蒂方程加以解决。