There are NN light bulbs indexed from 00 to N-1N−1. Initially, all of them are off.
A FLIP operation switches the state of a contiguous subset of bulbs. FLIP(L, R)FLIP(L,R)means to flip all bulbs xx such that L leq x leq RL≤x≤R. So for example, FLIP(3, 5)FLIP(3,5) means to flip bulbs 33 , 44 and 55, and FLIP(5, 5)FLIP(5,5) means to flip bulb 55.
Given the value of NN and a sequence of MMflips, count the number of light bulbs that will be on at the end state.
InputFile
The first line of the input gives the number of test cases, TT. TT test cases follow. Each test case starts with a line containing two integers NN and MM, the number of light bulbs and the number of operations, respectively. Then, there are MMmore lines, the ii-th of which contains the two integers L_iLi and R_iRi, indicating that the ii-th operation would like to flip all the bulbs from L_iLi to R_iRi , inclusive.
1 leq T leq 10001≤T≤1000
1 leq N leq 10^61≤N≤106
1 leq M leq 10001≤M≤1000
0 leq L_i leq R_i leq N-10≤Li≤Ri≤N−1
OutputFile
For each test case, output one line containing Case #x: y, where xx is the test case number (starting from 11) and yy is the number of light bulbs that will be on at the end state, as described above.
样例输入
2 10 2 2 6 4 8 6 3 1 1 2 3 3 4
样例输出
Case #1: 4 Case #2: 3
题意:
有T组样例,依次输入每组样例,第一行为n,表示有n个灯泡,然后m次操作,最后输出经过m次操作后亮着的灯泡有多少个?
思路:
首先,我们会想就操作区间的进行加1,最后n个数,依次代表n个灯泡操作的次数,次数%2==0,就是关着的,次数%2==1,就是开着的。
就拿第一个样例来说:
第一行:开始状态 第二行:第一次操作后 第三行:第二次操作后
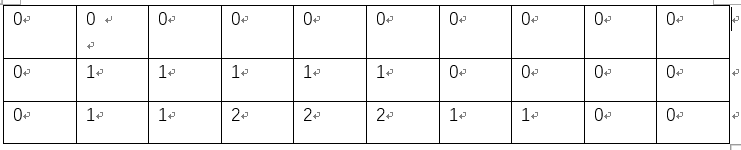
m次操作,每次是将区间的所有值都加一。
这里不是不有点前缀和的味道,给定 n 个数和 m 次询问,每次询问一段区间的和,一个 O(n + m) 的做法。
for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + a[i]; //O(n) while(m--) //O(m) { int L, R; scanf("%d%d", &L, &R); printf("%d ", sum[R] - sum[L - 1]); }
我们先简单的引入有关差分的概念。
设a数组表示原始的数组;
设d[i]=a[i]-a[i-1](1<i≤n,d[1]=a[1]);
设f[i]=f[i-1]+d[i](1<i≤n,f[1]=d[1]=a[1]);
设sum[i]=sum[i-1]+f[i](1<i≤n,sum[1]=f[1]=d[1]=a[1])。

这道题我们完全用差分
为了不出现负数的情况,我们可以初始化每个数都为1000(一千次操作),然后对区间操作的时候[l,r],将a[l]+1,a[r+1]-1,
然后我们直接进行求和
for(i = 1;i<=n;i++)
b[i] = b[i-1]+a[i];
b[i]%2==0灯就是关着的,b[i]%2==1灯就是开着的
但是还是不行,为什么呢?我们分析一下,每个样例我们都要对数组进行初始化1e6,然后我们对区间的端点进行操作m,然后最后来个类似于前缀和的操作1e6
所有大约1e3*2e6=2e9,两秒,题目要求一秒,超时,然后我们想到用空间换时间,这也是我之前想过的,不用想,直接爆,我太难了!!!
因此我们要再想一想如何优化,可以满足要求
既然我们是直接对区间的端点进行操作,那么我们想一想能不能把1e6转为1e3,这样1e3*1e3=1e6,不会超
显然是可以的。
这里是%2==1/0进行判断灯是否亮,前面差分我们是+1 ,-1(把对后面的影响抵消掉),但是对这一道题我们可以直接+1,+1,两次加1作用就抵消了,并且操作相同。
经过m次操作就直接输出结果,那么哪个操作在前,哪个操作在后其实就不重要了
我们记录端点(l,r+1),然后所有操作完后进行排序,从小到大,我们两两配对,从前往后,
2 4 7 9,
4-2 2相当于从第二个灯泡影响到最后的灯泡,4就把从第四个灯泡开始的影响给消除了,然后这一对操作其实影响的就只有2个灯泡,7-8类似
4-2+9-7=4.
代码:
#include<bits/stdc++.h> using namespace std; const int maxn = 1e6+20; int num[maxn*2]; int main(){ int t; cin>>t; for(int i=1;i<=t;i++){ int n,m; scanf("%d%d",&n,&m); int count = 0; for(int j = 0; j<m;j++){ int x,y; scanf("%d%d",&x,&y); num[count++] = x; num[count++] = y+1; } sort(num,num+m*2); int sum = 0; for(int i = 0;i <count;i+=2){ sum +=num[i+1] - num[i]; } printf("Case #%d: %d ",i,sum); } return 0; }