一 算法效率的度量方法
1 高级语言编写的程序在计算机上运行时所消耗的时间取决于以下因素:
- 算法采用的策略和方案
- 编译产生的代码质量
- 问题的输入规模(输入量的多少)
- 机器执行指令的速度
2 分析算法运行时间的关键:把基本操作的数量和输入模式关联起来
二 函数的渐进增长
1 定义:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。加上
2 技巧:判断一个算法的效率时,函数中的常数和其它次要项常常可以忽略,而更应该关注主项(最高项)的阶数。
三 算法时间复杂度
1 定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
2 表示:T(n) = O(f(n)) ,其中f(n)是问题规模n的某个函数
- 上式表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度
3 关键:执行次数=时间
4 大O记法:用大写的O()来体现算法的时间复杂度的记法
5 最优算法:随着输入规模n增大,T(n)增长最慢的算法
6 如何分析算法时间复杂度:
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行次数函数中,只保留最高阶项
- 如果最高阶项存在且不为1,则除掉与这个项相乘的常数
- 得到的最后结果就是大O阶
7:常数阶O(1)、线性阶O(n)、平方阶O(n^2)、对数阶O(log2n)
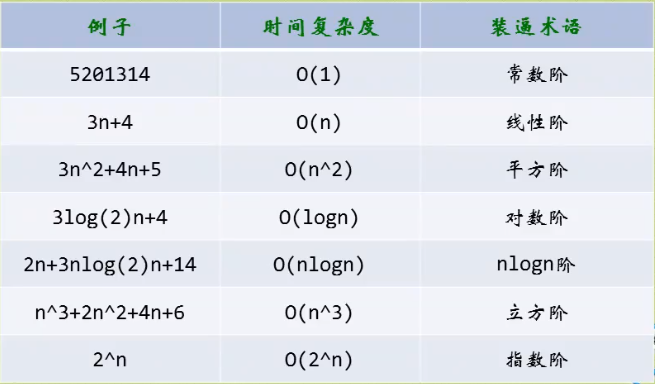
时间从小到大:O(1)<O(log2n)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
8 最坏的情况与平均情况
平均运行时间:期望的运行时间
最坏运行时间:在应用中,提到的运行时间一般都是最坏情况的运行时间
四 算法的空间复杂度
1 写代码完全可以用空间换时间,一般求复杂度都是指时间复杂度

2 表示 :s(n) = O(f(n)) 其中n是问题规模,f(n)是语句关于n所占存储空间的函数