目录
1.哈希
2.KMP
3.Trie
4.AC自动机
5.Manacher
6.回文自动机
哈希
哈希这东西只会一点点,真的一点点。
要用哈希来匹配两个字符串的话,一般都是用进制哈希。
首先设一个进制base,一般为131或13331,不容易出现冲突,然后给每种字符赋一个值,一般a为1,到z为26,将每个字母看做进制位上的一个数字来计算即可。
然后取一个大质数作为模数,每次再加一个质数,就可保证基本上没有冲突。
最后计算出字符串的hash值再比对就可以了。
代码实现
const int mod=1e9+7;
int base=131,p=1919810;
unsigned long long sum=0;
ull hash(char *a)
{
sum=0;
for(int i=0;i<n;i++)
{
sum=(sum*base+a[i]-'a'+1)%mod+p;
}
return sum;
}
KMP
KMP的核心内容我觉得只有一个,就是求最长border长度。
一个字符串的border就是找一个既是它的前缀又是后缀的字符串,最长的border长度顾名思义。
KMP的重点在于让模式串与文本串进行不断地匹配。一般会有一个 j,代表已经和模式串的 1 ~ j 匹配了,还有一个循环中的 i,与 1 ~ j 对应的就是文本串 i-j+1 ~ i的字符串。
循环时我们要比较 a[i+1] 和 b[j+1],看是否匹配,若匹配就让 j++,然后继续循环。
重点是不匹配怎么办,答案是让 j=p[j],也就是等于1~j的最长border长度。
可以想象一下,1 ~ j 与 i-j+1 ~ i相同,前缀与后缀相同。
所以,前缀=后缀=a对应字符串的后缀。也就在保证j定义同时减小了j。
这时候继续尝试匹配 a[i+1] 与 b[j+1] ,相同和之前一样,不相同则继续减小j,直到j为0。
如果仍然无法匹配,说明就找不到了,这时继续循环,看之后有没有文本串的哪一个字母会与模式串的第一个字符匹配,然后操作重复。
预处理时要求出模式串所有前缀的最长border长度,就只需要让模式串自己与自己匹配,通过之前求得的p进行递推,代码与AB匹配雷同。
参考博客:KMP算法详解
模板题:【模板】KMP字符串匹配
核心代码
void pre()
{
p[1]=0;
int j=0;
m=strlen(b+1);
for(int i=1;i<m;i++)
{
while(j>0&&b[i+1]!=b[j+1])j=p[j];
if(b[i+1]==b[j+1])j++;
p[i+1]=j;
}
}
void kmp()
{
n=strlen(a+1);
int j=0;
for(int i=0;i<n;i++)
{
while(j>0&&a[i+1]!=b[j+1])j=p[j];
if(a[i+1]==b[j+1])j++;
if(j==m){
printf("%d
",i+1-m+1);
}
}
}
Trie
学了一点皮毛,就只讲模板。
Trie 一般就只有2个操作,一个插入,一个查询。
由于 Trie 一般需要图才好理解,所以我给一个博客链接
插入首先需要一个指针 p,从根节点开始。根节点是空的。
就是在每一层放字符串里对应的字符,如果这一层已有相同的字母,就使 p 等于它的编号。如果没有,就新建一个节点,然后使 p 等于它的编号。
有一件循环结束后的事,就是要记录循环停止到的那个节点,用 end 数组标记一下,这样查询的时候我们就知道要匹配的字符串在此结束,匹配成功。
查询时同样从根开始,然后一层层去找要匹配的字母,有哪一层匹配不到就失败。如果用来匹配的字符串循环完了,就看那个位置有没有字符串结束,也即前面记录的 end 数组。
核心代码
int trie[N][26],tot=1;
int end[N];
void insert(char *s)
{
int len=strlen(s),p=1;
for(int i=0;i<len;i++)
{
int ch=s[i]-'a';
if(trie[p][ch]==0)trie[p][ch]=++tot;
p=trie[p][ch];
}
end[p]=1;
}
bool search(char *s)
{
int len=strlen(s),p=1;
for(int i=0;i<len;i++)
{
p=trie[p][s[i]-'a'];
if(p==0)return false;
}
return end[p];
}
AC自动机
自动机挺难的,我现在并不是非常理解,所以只能粗略地讲。
AC自动机都说是 Trie+KMP,我觉得的确如此。形象的说就是在树上KMP。
Trie的部分是简单的,只要会插入与查询两种操作就可以了,插入部分与正常的Trie并没有不同,至于查询就是根据题目要求改动,套一层循环即可。
AC自动机的重点在于失配数组,即 fail 数组。和KMP思想类似,fail 指向的地方就是匹配失败要转向的地方。
fail 指针的用途讲了,还要知道它的含义是什么,它指向的是当前字符串的最长后缀的所在地。
当前字符串指的是从Trie的根一直到当前匹配到的位置连起来形成的字符串,指向的点与根形成的字符串就是它的最长后缀。
那么 fail 该怎么求呢?
回顾 KMP ,会发现它的 p 数组是通过递推的方法求得的。fail 数组与 p 数组本质相同,所以我们要求 fail ,也需要从上往下,通过广搜的方式。
我们先假设在求 fail[trie[u][0]]。u为当前从队列中取出的节点,0~25 分别代表a至z。
先看 trie[u][0] 这个节点存不存在,如果存在,就让 fail[trie[u][0]]=trie[fail[u]][0] 。
想一想,fail 数组由于指向的是最长后缀,所以两个位置的字符相同。而显然,而我们要求出 fail 的节点因为 fail 的要求最长后缀,所以它的 fail 连向的节点的上一个节点肯定与它的父节点的字符相同。
理解之后继续。有人也许问如果父节点的 fail 指向的节点不包括要匹配的字符怎么办。这时候就涉及到我们的另一步。
如果 trie[u][0] 这个节点不存在,也就是说没有连接,我们要让 trie[u][0]=trie[fail[u]][0] 。
也就是说,如果这个节点不存在,让它等于父节点的 fail 指向的那个节点的相同字符的儿子。如果指向的那个节点也没有呢?那它的儿子也等于由它父节点的 fail 得到的节点。
这就等同于在跳 fail 了,如果哪一个 fail 跳到的节点的儿子匹配上了,就可以了,否则就一直跳到根。
联想一下节点存在时的代码,我们就可以理解了。这里的 trie[fail[u]][0] 其实就已经是经过多次跳 fail 后匹配得到的结果。
会求 fail 之后,其他的问题都不是什么困难了。
看一道模板题
简单版的,不用考虑太多。注意一点,可能会有重复的,这也需要统计,所以 end 数组必须是 int 类型的。
查询的时候每次循环,都从当前节点开始跳 fail ,直到为 0。取走 end 内的值之后做个标记,以后就不走这里。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int N=1e6+10;
int n,tot;
char s[N];
int end[N];
struct node{
int vis[26];
int fail;
}trie[N];
void insert(char *s)
{
int len=strlen(s),p=0;
for(int i=0;i<len;i++)
{
int ch=s[i]-'a';
if(trie[p].vis[ch]==0)trie[p].vis[ch]=++tot;
p=trie[p].vis[ch];
}
end[p]+=1;
}
void pre()
{
queue<int>q;
for(int i=0;i<26;i++)
{
if(trie[0].vis[i]){
trie[trie[0].vis[i]].fail=0;
q.push(trie[0].vis[i]);
}
}
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=0;i<26;i++)
{
if(trie[u].vis[i])
{
trie[trie[u].vis[i]].fail=trie[trie[u].fail].vis[i];
q.push(trie[u].vis[i]);
}
else trie[u].vis[i]=trie[trie[u].fail].vis[i];
}
}
}
int ans;
void search(char *s)
{
int len=strlen(s),p=0;
for(int i=0;i<len;i++)
{
int ch=s[i]-'a';
p=trie[p].vis[ch];
for(int k=p;k&&end[k]!=-1;k=trie[k].fail)
{
ans+=end[k];
end[k]=-1;
}
}
}
int main()
{
scanf("%d",&n);
while(n--)
{
scanf("%s",s);
insert(s);
}
pre();
scanf("%s",s);
search(s);
printf("%d",ans);
return 0;
}
参考资料:
1.yyb的博客
Manacher
不太会,简单讲一讲。
其实要先分为奇回文串和偶回文串两种情况,因为两种情况的对称中心不同。因为偶回文串的对称中心是间隔,所以为了方便,我们需要在每两个字符之间加一个额外的字符(不在题目字符串可能出现的字符范围内)。
其次来讲怎么求最长回文串。核心思想是利用递推求出每个字符作为对称中心时,可以向两边扩展出的最大回文串长度,然后取最大值。
因为字符间隔也可以是对称中心,之前的预处理这时就发挥效用了。
这里以 mr 作为已经触及到的最右边的位置,即某个字符作为中心向右扩展到的最远的地方。以及一个 mid 代表与 mr 对应的那个中心。然后用 hw[i] 代表以 i 作为中心可扩展出的最大回文串长度。
首先考虑 hw[i] 的初值,假设 mid<i<mr ,那么必然有一个 j 在 mid 左边与 i 对称。这里我们设 x 为 mr 关于 mid 的对称点。
如果 j 左边扩展到的地方没有越过 x ,那么根据对称性 hw[i] (ge) hw[j]。
但是若 j 左边扩展过了 x,那么对应的 i 右边就过了 mr,属于未知领域,所以还得有一个限制,那就是 hw[i] 的最大初值: mr-i 。这个情况就相当于 j 左边刚好顶在了 x 上,属于极限情况。
没有 i<mid 的情况,i 毕竟是递进的,mid 的值既然从以前的 i 得来,就必然小于现在的 i。
若是 i(ge)mr,那么 hw[i]=1。
赋初值的工作完成以后,其他的事情都变得简单了。先用 while 循环进行一头一尾字符的匹配,hw[i] 增大直到匹配不了。
最后判断一下 i 的右边界是否超过了 mr ,是的话更新 mr 与 mid 即可。
还有一个要知道的是,因为字符串中包括了代表间隔的字符,所以 hw[i] 并不用乘二,并且由于 while 循环结束时会让 hw[i] 多加 1,所以输出时要减回去。
AC代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 51000010
using namespace std;
int hw[N],n,ans;
char a[N],s[N<<1];
void manacher()
{
int mr=0,mid;
for(int i=1;i<n;i++)
{
if(i<mr)hw[i]=min(hw[(mid<<1)-i],hw[mid]+mid-i);
else hw[i]=1;
while(s[i+hw[i]]==s[i-hw[i]])hw[i]++;
if(i+hw[i]>mr)
{
mr=i+hw[i];
mid=i;
}
}
}
void change()
{
s[0]=s[1]='#';
for(int i=0;i<n;i++)
{
s[i*2+2]=a[i];
s[i*2+3]='#';
}
n=n*2+2;
s[n]=0;
}
int main()
{
scanf("%s",a);
n=strlen(a);
change();
manacher();
ans=1;
for(int i=0;i<n;i++)
ans=max(ans,hw[i]);
printf("%d",ans-1);
return 0;
}
参考资料:
1.模板题题解之一
回文自动机(PAM)
虽然都是自动机,但是与AC自动机不同,回文自动机的核心代码跟 manacher 一样短。
虽然核心代码很短,但是它的思想却需要一段时间去理解。
首先我们先来考虑如何建 Trie。回文自动机的 Trie 和普通的不同,它被称为回文树。而且通常有两个根,一个连接的字符串代表的是奇回文串,另一个则是偶的。
我们就先用模板题的第一个样例作为例子。
先上图
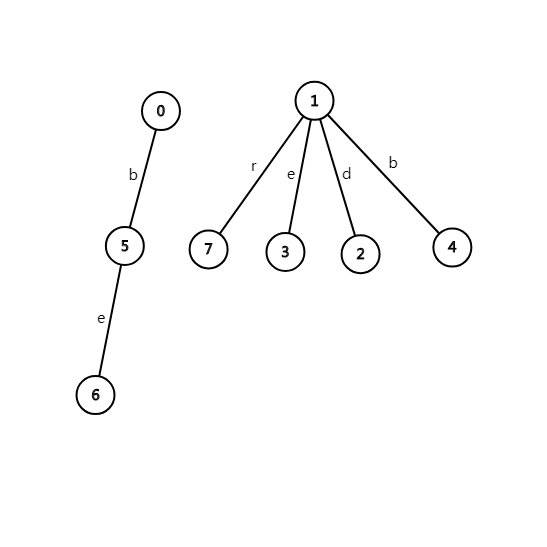
如图,1 连接的是奇回文串,0 连偶回文串。回文树有一个特点,就是它每个节点代表的字符串都是从下往上读的。比如 6 号节点代表的就是 ebbe 这个回文串。
我们先想一想该怎么新建节点。假设我们已经匹配到了 s[i-1] ,现在要加上 s[i] ,那么就需要对 s[i] 与之前的字符串形成的新的回文串新建点。
但是是所有的新回文串吗?考虑一下,我们发现只需要给新出现的最长的回文串建点就行了。其余短的新回文串都是它的子串,因为回文串的对称性,所以这些子串在之前就已经出现过了,无需新建。
顺便还证明了一棵回文树最多只有 n+2 个点。(n 为读入的字符串长度)
那么具体该怎么建呢?我们首先要找到它的父节点。(用 len[x] 代表 x 节点代表的回文串长度)先考虑一个情况:如果 s[i-len[x]+1] 到 s[i] 是一个回文串,那么显然 s[i-len[x]+2] 到 s[i-1] 也是一个回文串。
现在我们既然要加上 s[i] ,自然也就要保证 s[i]=s[i-len[x]+2] 。当然,这里的 len[x] 实际是属于 s[i] 对应的节点的,实际的 len[x] 对应的应该是 s[i-1] 。所以我们在匹配时要保证的实际是 s[i]=s[i-len[x]-1]。
然后就要介绍我们熟悉的 fail 数组。在这里它指向的就是当前字符串的最长回文后缀代表的节点。如果不能匹配,就利用 fail 数组进行转移,直到成功,因为单个字符也能是回文串,所以不存在失败。
fail 数组当然是通过递推的方式求。先给出代码: fail[tot]=trie[getfail(fail[pos],i)][s[i]-'a']。
这看起来非常费解,没关系,我们一个个来。首先是 getfail ,它其实是一个函数,就是我们上面用来匹配找父节点的函数,这里也是同样的功效。
getfail函数实际长这样
int getfail(int x,int i)
{
while(i-len[x]-1<0||s[i-len[x]-1]!=s[i])x=fail[x];
return x;//i-len[x]-1可能小于0,特判处理
}
如果你很好的理解了AC自动机中求 fail 的代码段,那么这里求 fail 的方式也不会难理解。道理和AC自动机一样,只不过AC自动机因为广搜将跳 fail 拆成了一步又一步,而在这里是直接跳 fail,找到拥有相同儿子的父节点。
pos 代表的是我们之前通过 getfail 函数找到的父节点。而这里套了个 fail 在外面是为了防止它把自己当成最长后缀。
有一个初始化要铭记:fail[1]=0,fail[0]=1 。这是为了防止找不到匹配,让 fail 可以跳到另一个根上。
接下来看一下完整的循环代码吧。
for(int i=0;i<n;i++)
{
if(i>0)s[i]=(s[i]-97+last)%26+97;
pos=getfail(cur,i);
int ch=s[i]-'a';
if(!trie[pos][ch])
{
fail[++tot]=trie[getfail(fail[pos],i)][ch];
trie[pos][ch]=tot;
len[tot]=len[pos]+2;
num[tot]=num[fail[tot]]+1;
}
cur=trie[pos][ch];
last=num[cur];
printf("%d ",last);
}
剩下没讲的地方就是 cur 了。它代表的其实是当前所在节点,每次更新,这样给 s[i] 进行匹配时的 len[x] 也可以随之更新。
建新节点时不要忘记 len 数组。因为是回文串,所以树上的一个字符是两个长度。而与 1 号根相连的第一个字符因为只有一个,所以 len[1] 要初始化为 -1 。
多余的部分,比如 num 是记录在这个位置结束的回文串的个数。last 是答案,以及最开头对 s[i] 的更新,都是针对题目的,并非普遍适用。
讲完了,逻辑可能有点混乱,总体应该还好。
最后放一下完整代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=2e6+10;
char s[N];
int num[N],fail[N],trie[N][26],len[N];
int cur,pos,last,tot=1,n;
int getfail(int x,int i)
{
while(i-len[x]-1<0||s[i-len[x]-1]!=s[i])x=fail[x];
return x;
}
int main()
{
scanf("%s",s);
n=strlen(s);
fail[0]=1;len[1]=-1;
for(int i=0;i<n;i++)
{
if(i>0)s[i]=(s[i]-97+last)%26+97;
pos=getfail(cur,i);
int ch=s[i]-'a';
if(!trie[pos][ch])
{
fail[++tot]=trie[getfail(fail[pos],i)][ch];
trie[pos][ch]=tot;
len[tot]=len[pos]+2;
num[tot]=num[fail[tot]]+1;
}
cur=trie[pos][ch];
last=num[cur];
printf("%d ",last);
}
return 0;
}
参考资料:
1.功在不舍的模板题题解