1 对称矩阵
当矩阵中所有元素均为实数时,满足 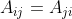 时,该矩阵为对称矩阵
时,该矩阵为对称矩阵 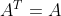 ; 其特征值均为实数,特征向量相互正交。
; 其特征值均为实数,特征向量相互正交。
特征值为实数证明如下:
![]() ,两边同时取共轭得
,两边同时取共轭得 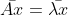 ,
, ,
,
由于 A 为实矩阵,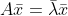 ,由于 A 为对称矩阵,两边转置后得
,由于 A 为对称矩阵,两边转置后得 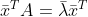 ,
,
两边同时乘 x 得 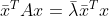 ,
,
对  两边同时乘
两边同时乘 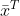 得
得  ,
,
对比 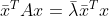 与
与  得
得  ,故
,故 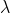 为实数;
为实数;
特征向量相互正交证明如下:
假设有两特征向量满足 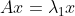 ,
, ,
,
要证明两向量正交,需要构造 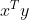 表达式,通过矩阵 A 可建立如下联系:
表达式,通过矩阵 A 可建立如下联系:
 ,
, ,
,
由于特征值为实数且不相等, 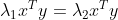 ,
,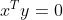 ,故特征向量相互正交;
,故特征向量相互正交;
2 Hermitian 矩阵
在复平面上,向量 x 得长度定位为 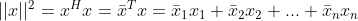 ,
,
向量 x,y 正交定义为 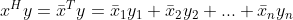 ,
,
如果  ,该矩阵为复数域中的对称矩阵,被称为 Hermitian 矩阵,
,该矩阵为复数域中的对称矩阵,被称为 Hermitian 矩阵,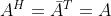 ;
;
由于实数域是复数域的一个子集,实数域中的对称矩阵也是复数域中的 Hermitian 矩阵;Hermitian 矩阵的特征值为实数,特征向量相互正交。
特征值为实数证明如下:
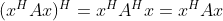 ,由于
,由于 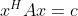 ,c 为一复数,
,c 为一复数,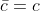 ,c 为一实数,
,c 为一实数,
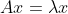 ,
,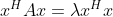 ,
, ,
,
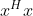 为特征向量的模长,该模长为一实数,且特征向量不为零使得
为特征向量的模长,该模长为一实数,且特征向量不为零使得 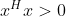 ,故特征值为实数;
,故特征值为实数;
特征向量相互正交证明如下:
假设有两特征向量满足 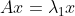 ,
, ,
,
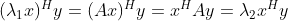 ,
,
由于特征值为实数,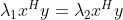 ,由于
,由于 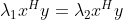 ,由于
,由于  ,
,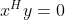 ,两特征向量正交;
,两特征向量正交;
当矩阵有充足的特征向量,矩阵 A 可被分解为  ,由于矩阵A为 Hermittan矩阵(或对称矩阵),其特征向量正交,将其归一化后得 :
,由于矩阵A为 Hermittan矩阵(或对称矩阵),其特征向量正交,将其归一化后得 :
 ,矩阵 A 被分解为 n 个 Rank 1 矩阵得线性和。
,矩阵 A 被分解为 n 个 Rank 1 矩阵得线性和。
3 斜对称矩阵
当矩阵中所有元素均为实数时,满足 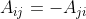 时,该矩阵为对称矩阵
时,该矩阵为对称矩阵 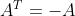 ; 其特征值均为纯虚数,特征向量相互正交。
; 其特征值均为纯虚数,特征向量相互正交。
特征值为纯虚数证明如下:
与对称矩阵特征值为实数证明类似,![]() ,
, ,
,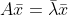 ,
,
两边转置得 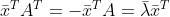 , 两边同时乘 x 得
, 两边同时乘 x 得 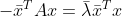 ,
,
对  两边同时乘
两边同时乘 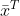 得
得  ,
,
对比 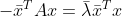 与
与  得
得 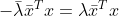 ,
,
由于特征向量不为零,有 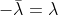 ,故特征值为纯虚数;
,故特征值为纯虚数;
特征向量相互正交证明如下:
对称矩阵特征向量相互正交证明类似,假设有两特征向量满足 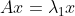 ,
, ,
,
要证明两向量正交,需要构造 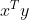 表达式,通过矩阵 A 可建立如下联系:
表达式,通过矩阵 A 可建立如下联系:
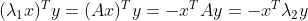 ,
, ,
,
由特征值不为零得 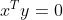 ,故特征向量相互正交;
,故特征向量相互正交;
4 Skew Hermittan 矩阵
当矩阵中元素包含复数时,如果 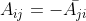 ,
,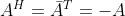 ,该矩阵为 Skew Hermittan 矩阵。其特征值为纯虚数,特征向量正交。
,该矩阵为 Skew Hermittan 矩阵。其特征值为纯虚数,特征向量正交。
由 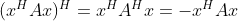 得
得  为纯虚数,
为纯虚数, 表示向量模长的平方,为实数,
表示向量模长的平方,为实数,
在 Hermittan 矩阵中  ,故特征值为纯虚数;
,故特征值为纯虚数;
假设有两特征向量满足 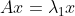 ,
, ,
,
 ,
,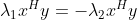 ,
,
由特征值不为零得 ![]() ,故特征向量相互正交;
,故特征向量相互正交;
5 酉矩阵(正交矩阵)
如果矩阵 A 中每列向量相互正交且为单位长度,如果矩阵中各元素均为实数时为正交矩阵,如果矩阵中存在复数为酉矩阵;
酉矩阵与正交矩阵性质基本一致,其证明过程也基本一致,下面给出酉矩阵性质及证明:
1)酉矩阵不改变向量点积与长度;
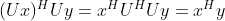 ,
,
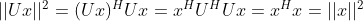 ;
;
2)酉矩阵特征值绝对值为 1;
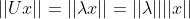 ,由于性质 1)
,由于性质 1) ,
,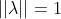 ;
;
3)酉矩阵特征向量正交;
假设 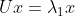 ,
,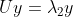 ,
,
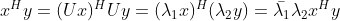 ,
,
由于 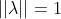 ,且
,且 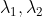 为不同特征值,因此
为不同特征值,因此 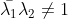 ,故
,故  ,特征向量正交;
,特征向量正交;
参考资料 Linear Algebra And Its Applications Gilbert Strang