一 简介
在视频成像中,有部分视频存在不确定抖动(如眼球颤抖),可以使用光流方案计算出整个视频的运动速度 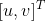 ,剔除抖动,实现视频稳像。
,剔除抖动,实现视频稳像。
当物体运动时,每一个点的运动方向构成了物体的运动场。物体在图像上形成的亮度模式相应改变,称为光流。在一般情况下,运动场与光流基本是一致的,所以可以通过光流来估计图像运动。
通过数学建模,光流可表示为图像空域差分(XY平面梯度)与图像帧间差分(相邻两帧图像差)的函数。理想情况下,我们可以计算出图像上每一个点的运动速度,但存在两点问题:
1)光滑平面上图像空域差分与图像帧间差分均为0,故计算出光流速度为0;
2)在图像边缘上,由于光流计算观察一个较小邻域,无法计算出边缘方向上的运动速度(即孔径问题)。
因此,需要对特殊点进行光流计算以避免以上问题。该特殊点称为角点,角点在邻域上至少两个方向上存在明显梯度变化,这就避免了孔径问题。同时,在图像匹配应用中,角点或者类似的特 征点也是多幅图像之间关联点。
二 Harris角点
考虑一个固定小的图像区域,相对于该图像区域做任意一个小的平移  ,其变化量可用自相关函数定义:
,其变化量可用自相关函数定义:
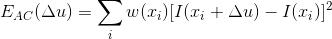 ,其中
,其中 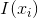 表示固定小的图像区域内的点,
表示固定小的图像区域内的点,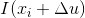 表示对其进行任意平移后的点,
表示对其进行任意平移后的点,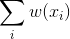 表示对区域内求所有点加权和。
表示对区域内求所有点加权和。
对于该公式需要注意以下两点:
1)对于图像上任意一个固定点,其变化量随着  的取值不同而不同,但该点作为角点的性质取决于图像邻域数据本身。也就是说,如果考察点为角点,使用不同方向的
的取值不同而不同,但该点作为角点的性质取决于图像邻域数据本身。也就是说,如果考察点为角点,使用不同方向的 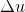 代入上式,其变化量在两个正交方向上都会得到较大值;如果考察点为边缘,则仅在边缘梯度方向上表现为较大值;如果考察点为平滑区域,则在每个方向上都没有较大值。
代入上式,其变化量在两个正交方向上都会得到较大值;如果考察点为边缘,则仅在边缘梯度方向上表现为较大值;如果考察点为平滑区域,则在每个方向上都没有较大值。
2)图像梯度函数为  ,当两个梯度分量都较大时,该点可能是角点,也可能不是角点。比如,斜率为45度角的直线,在两个方向上均有较大梯度,但不是角点。总的来说,这两个概念是两个不同的测量。
,当两个梯度分量都较大时,该点可能是角点,也可能不是角点。比如,斜率为45度角的直线,在两个方向上均有较大梯度,但不是角点。总的来说,这两个概念是两个不同的测量。
对以上公式进行数学变换:
假设图像函数在 (x,y) 平面上连续且二阶可导(图像一般满足该性质),针对较小变化量 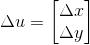 ,
,
由于图像某一点梯度为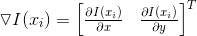 , 对
, 对 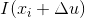 进行泰勒级数展开,
进行泰勒级数展开,
可得  ,其中 e 为二阶及以上高阶分量,可忽略并简化为:
,其中 e 为二阶及以上高阶分量,可忽略并简化为:
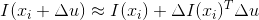 ,对 自相关函数 使用泰勒级数得:
,对 自相关函数 使用泰勒级数得:
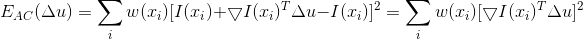 ,
,
 ,进一步整理得:
,进一步整理得:
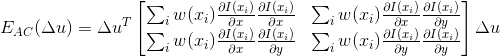 ,
,
则固定小区域的自相关矩阵为: 。
。
自相关矩阵A包含对应区域的变化的全部信息,通过分析该矩阵,可以判断相应区域是否为角点区域。
由于 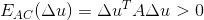 , 则矩阵A为正定矩阵,矩阵A存在两个正交的特征向量,将矩阵A可分解为:
, 则矩阵A为正定矩阵,矩阵A存在两个正交的特征向量,将矩阵A可分解为:
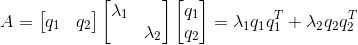 , 其中
, 其中 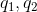 为矩阵A的单位特征向量,自相关变量可进一步表示为:
为矩阵A的单位特征向量,自相关变量可进一步表示为:
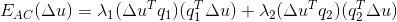 ,当
,当 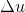 与
与 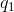 共线时,
共线时,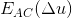 取值为
取值为  ;
;
当 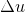 与
与 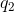 共线时,
共线时,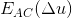 取值为
取值为 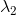 。也就是说,
。也就是说, 在特征向量方向上取值取决于对应特征值。
在特征向量方向上取值取决于对应特征值。
在其他方向上,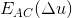 取值介于两个特征值之间。为了确保区域为角点,考察较小特征值大于某个阈值即可。
取值介于两个特征值之间。为了确保区域为角点,考察较小特征值大于某个阈值即可。
另外,如果将 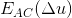 分解为关于x,y的函数,发现
分解为关于x,y的函数,发现 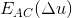 实际上为 关于x, y的二次函数,即一个向上的抛物面。
实际上为 关于x, y的二次函数,即一个向上的抛物面。
令 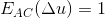 ,则得到一个椭圆平面,其长轴表示变化最快方向,其短轴表示变化最慢方向,当椭圆接近圆形时,该区域则为较好的角点区域。
,则得到一个椭圆平面,其长轴表示变化最快方向,其短轴表示变化最慢方向,当椭圆接近圆形时,该区域则为较好的角点区域。
在实际计算中,一般不直接计算出特征值,而是通过矩阵的行列式与矩阵的迹来判断是否为角点区域,如:
1) ;
;
2) 。
。
三 Lucas-Kanade光流
LK光流基于以下假设:
1)被追踪点帧间亮度保持恒定;
2)被追踪点帧间移动较小;
3)被追踪点邻域运动一致。
根据假设1),可得:
 ,对
,对  进行一阶泰勒展开:
进行一阶泰勒展开:
 ,
,
根据假设 2),帧间移动距离较小,也即帧间间隔时间较短,令 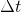 趋近于 0, 消除冗余并同时除以
趋近于 0, 消除冗余并同时除以  得:
得:
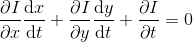 ,其中
,其中 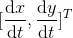 表示光流运动。
表示光流运动。
上式表明,被追踪点的运动速度 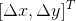 由图像梯度与帧间差分约束,我们无法通过上式求出被追踪点的运动速度。
由图像梯度与帧间差分约束,我们无法通过上式求出被追踪点的运动速度。
根据假设3),由于被追踪点邻域运动一致,对邻域点做相同计算,并建立其联立方程组,即可求解被追踪点的运动速度。
理论上来说,只需要两个线性不相关的方程即可求解光流速度。实际应用中,可以对邻域内每一个点建立方程,构成超定的(overdetermined)线性方程组,从而提升计算准确度,超定线性方程组求解为: 。
。
以上建立了光流跟踪的一般方法。方程组 Ax = b 具体表示为 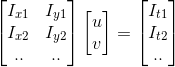 ,
,
 具体表示为
具体表示为  ,矩阵
,矩阵 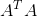 决定了方程是否存在准确解;
决定了方程是否存在准确解;
当矩阵 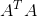 可逆时,方程组有确定解。在角点检测中,当自相关矩阵存在两个较大的特征值时,该点被认作角点;此时的自相关矩阵是可逆的,接近正定矩阵。这也是光流跟踪所需要的良好条件。
可逆时,方程组有确定解。在角点检测中,当自相关矩阵存在两个较大的特征值时,该点被认作角点;此时的自相关矩阵是可逆的,接近正定矩阵。这也是光流跟踪所需要的良好条件。
对于邻域大小选择,当选择邻域较大时,可能违背 邻域运动 一致性原则;当选择邻域较小时,可能遇到孔径问题,而良好角点正好可以在较小邻域上避免孔径问题。
总的来说,Harris 角点特性正好避免 LK 光流跟踪约束方程的孔径问题,所以,使用 LK 算法跟踪 Harris 角点可以获得较好的结果。
在Learning OpenCV中,给出了一维图像的光流计算解释,这可以更直观理解光流计算,具体如下:
针对一维图像,有 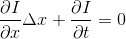 ,其中
,其中 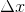 为一维图像的光流速度,则
为一维图像的光流速度,则 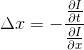 ,其图形如下:
,其图形如下:
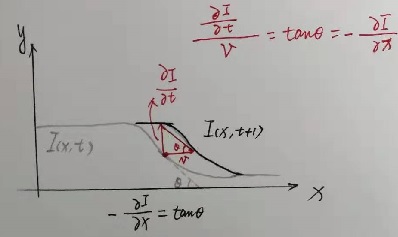
使用 Newton 插值方法可以进一步精确光流速度,如下图:

在实际应用中,LK光流假设2)会经常难以满足,使用图像金字塔可以跟踪帧间较大移动。首先在顶层金字塔上估计光流运动,然后在下一层金字塔中使用上层运动进一步精确光流运动。
在OpenCV中,使用 cv::goodFeaturesToTrack 提取角点,在精确度要求较高时,可使用 cv::CornerSubPix 对提取到的角点计算亚像素精度,该算法基本思想是边缘上点与角点的连线垂直于边缘上点梯度方向;然后使用函数 cv::calcOpticalFlowPyrLK 对提取的角点在两帧图像上计算对应的光流速度;最后,由于部分点的光流速度可能受到干扰影响,可以使用统计的方法剔除部分掉。
参考资料 :Learning OpenCV 3 Adrian Kaehler & Gary Bradski
Computer Vision: Algorithms and Applications Richard Szeliski