SRM-697-DIV2

Div2 Medium: DivisibleSetDiv2

Problem Statement

You are given a vector <int> b containing a sequence of n positive integers: b[0], ..., b[n-1]. We are now looking for another sequence a[0], ..., a[n-1]. This sequence should have the following properties:

• Each a[i] should be a number of the form 2^x[i] where x[i] is some positive integer. In other words, each a[i] is one of the numbers 2, 4, 8, 16, ...
• For each i, the value a[i]^b[i] (that is, a[i] to the power b[i]) should be divisible by P, where P is the product of all a[i].

Determine whether there is at least one sequence with the desired properties. Return "Possible" (quotes for clarity) if such a sequence exists and "Impossible" otherwise.

Definition

Class:	DivisibleSetDiv2
Method:	isPossible
Parameters:	vector <int>
Returns:	string
Method signature:	string isPossible(vector <int> b)
(be sure your method is public)

Limits

Time limit (s):	2.000
Memory limit (MB):	256
Stack limit (MB):	256

Constraints

-

b will contain between 1 and 50 elements, inclusive.

-

Each element in b will be between 1 and 10, inclusive.

Examples

0)

{3,2}

Returns: "Possible"

One valid sequence is the sequence {2, 2}. That is, a[0] = a[1] = 2. Clearly, each a[i] is a power of two not smaller than 2. The product of all a[i] is 2*2 = 4. Both a[0]^b[0] = 2^3 = 8 and a[1]^b[1] = 2^2 = 4 are divisible by 4.

1)

{3,3,3}

Returns: "Possible"

Here, one valid sequence is {2, 2, 2}.

2)

{1,10}

Returns: "Impossible"

Suppose that a[0] = x and a[1] = y. The value a[0]^b[0] = x^1 should be divisible by x*y. This is only possible for y = 1. However, 1 is not a positive power of two, so we cannot have a[1] = 1.

3)

{2, 3, 10}

Returns: "Possible"

One valid sequence is {8, 4, 2}.

4)

{7,10,4,6,3}

Returns: "Possible"

5)

{9,9,9,9,9,9,9,9,9}

Returns: "Possible"

6)

{3,4,5,6,7}

Returns: "Impossible"

　　This is a mathematical problem which is very simple to implement but hard to prove. It turns out that the answer is "Possible" if and only if ∑i=0n−11bi≤1∑i=0n-11bi≤1. You can find a detailed proof below.

　　We are asked if there exists a sequence of powers of two (a0,a1,...,an−1)(a0,a1,...,an-1) that for every i:

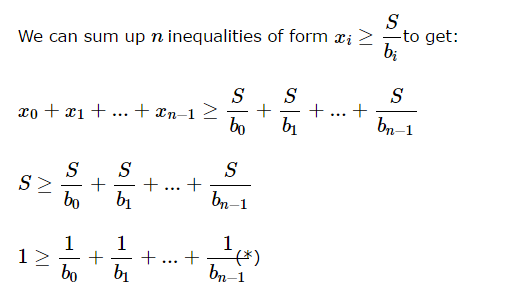
　　Finally, we should avoid losing accuracy in order to use the perfect formula. Casuing the range of bi is [1, 10], we can multiply a constant C which equal to LCM(1,...,10). 

public string isPossible(vector<int> b) {
  int LCM = 2520, sum = 0;
  for (int bi : b)
    sum += LCM / bi; // sum up 1/b multiplied by LCM to avoid floats
  return (sum <= LCM) ? "Possible" : "Impossible";
}

　　Recently, I had met two mathematical problems. The last one is hihoCoder_5 using log to get the maximum value. 

____+++++____