算法导论之插入排序和归并排序

　　作为一名前线的码农不时地看一下算法和数据结构还是很有必要的，虽然《算法导论》这本书很难啃，但还是有必要啃一下的。算法这东西和某种编程语言关系不大，在大学的课堂上书上一般是用伪代码来描述算法的，而用C语言去实现。算法更多的是一种思想，一种解决问题的方法，多看看算法还是很有必要的，它可以开阔的你的思路，让你在编程时思维更为活跃。

　　当然了，本人在算法方面水平有限，这不正在努力的学习不是，接下来就按算法导论上描述的插入排序和归并排序使用Objective-C语言实现一下，当然用什么语言是次要的，关键是理解算法才是关键。

　　一、创建我们的测试工程

　　　　因为我们只理解相应算法，没有什么用户图形，也就用不到UI了，在这儿使用Xcode创建一个基于Mac开发的控制台工程即可，整个工程很简单，一个main函数一个排序类，如下所示。

　　　　在Sort类中我们写了关于排序的一些类方法，然后在main函数中进行调用。

 

　　二、插入排序

　　　　插入排序顾名思义，就是把无序的元素插入到有序的元素当中。《算法导论》中举了一个特为形象的例子，插入排序就如同你在打扑克时摸牌一样，手里的牌是有序的，而你刚摸得牌是是随机的，需要你插入到已经排好序的扑克牌中，这就是插入排序。

　　　　如果用代码实现的话就是每经过一轮插入排序后，前面有序的元素就会加一，而后面无序的元素就会减一。下面根据Demo的实例来说明一下插入排序的思路和具体实现方式。

　　　　1.因为在OC中的可变数组是引用类型，所以在函数中改变后不需要返回。

　　　　2.因为数组中只有一个数据的时候它就是有序的，所以前面有序数列的初始有一个数据，也就是原始数组中的第一个数据。我们从下标为1开始遍历每个无序的元素，往前面有序的元素中相应的位置插入该元素，但插入后必须保证有序数组依然是有序的。

　　　　3.我们需要把即将插入到有序序列的数据进行暂存，因为有序序列中大于当前要插入数据的元素需要后移，为元素插入做准备。有序元素的移动会覆盖的要插入的元素，所以必须得暂存。

　　　　4.遍历有序序列，找到合适的插入位置，进行元素的插入。

+(void) insertionSortWithArray: (NSMutableArray *) array{
    
    //从第二个数开始往前面的数据中进行插入，每经过一轮外面的循环，前面就插入一个从后面取出的值，
    //因此没经过一轮外层循环，有序序列的长度就增加一
    for (int i = 1; i < array.count; i ++) {
        
        //暂存将要插入到前方的数据
        NSNumber *key = array[i];
        
        //获取有序序列最后一个元素的下标
        int j = i - 1;
        
        //循环遍历有序序列，寻找合适的数据插入位置，在此过程中，为数据的插入腾出位置，也就是把
        //比将要暂存的数据大的元素向后移动
        while (j >= 0 && array[j] > key) {
            
            array[j+1] = array[j];
            
            j--;
        }
        
        //插入数据
        array[j+1] = key;
        
        NSLog(@"第%d轮插入排序结果如下：", i);
        [self displayArrayWithArray:array];

    }
}

 　　　　displayArrayWithArray是事先写好的输出数组中数据的方法，代码如下，该方法是把数组元素拼接成字符串，然后进行输出。

+(void) displayArrayWithArray: (NSMutableArray *)array{
    
    NSMutableString *strTemp = [NSMutableString string];
    for (int i = 0; i < array.count; i++) {
        [strTemp appendFormat:@"%@, ", array[i]];
    }
    NSLog(@"%@

", strTemp);
}

　　　　接下来，让我们在main函数中使用随机数产生一个随机的数组，然后进行测试，如下：

        //生成测试随机数组
        NSMutableArray *array = [[NSMutableArray alloc] init];
        UInt count = 10;
        for (int i = 0; i < count; i ++) {
            NSNumber *temp =  @(arc4random()%100);
            [array addObject:temp];
        }

　　进入测试阶段，调用displayArrayWithArray方法，打印随机生成的原始数组，然后调用插入排序，如下所示：

        NSLog(@"原始数组如下：");
        [Sort displayArrayWithArray:array];
        
        //插入排序
        [Sort insertionSortWithArray:array];

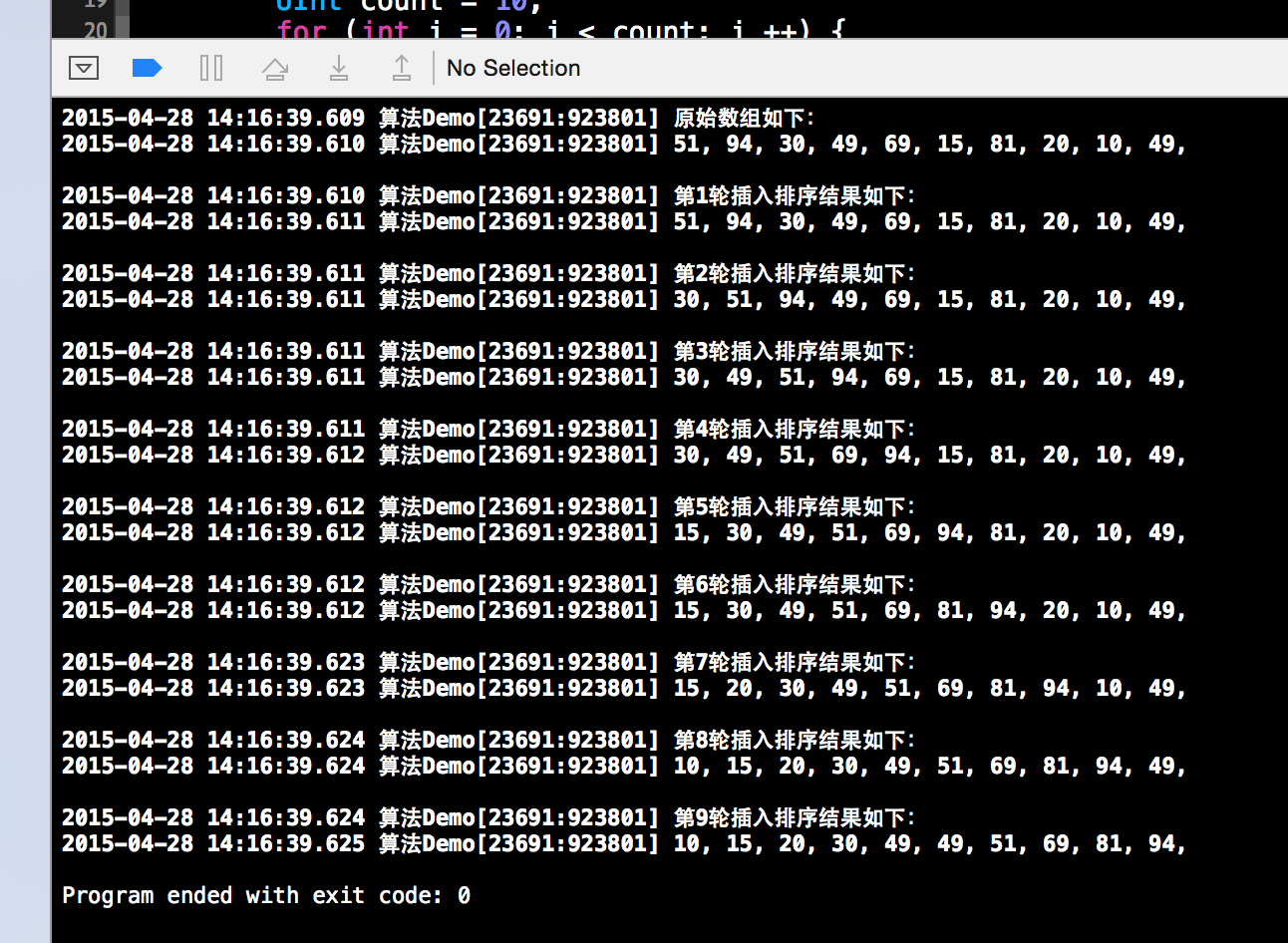
　　输入结果如下,排序方式如下，一目了然，第一轮是前面两个有序，第二轮是前面3个有序，以此类推，该算法的复杂度是O(n²)的

　　三、归并算法

　　　　归并算法之所以有归并是因为把原来的问题分解成更小的子问题，然后子问题解决要比原问题更为简单一些，把子问题的解进行有效的合并，然后得到整个问题的解。这就是分而治之的思想。

　　　　接下来将要具体的实现归并排序算法。

　　　　1.首先实现归并部分的代码，进行归并的数组是已经排好序了的，下面是把数组进行合并的代码，如下：

//一次归并
+(void) mergeWithArray: (NSMutableArray *)array
         WithStarIndex: (NSInteger) starIndex
          WithMidIndex: (NSInteger) midIndex
          WithEndIndex: (NSInteger) endIndex
{
    //记录归并次数
    static int sort_count = 0;
    
    if (endIndex < starIndex) {
        return;
    }
    
    //前半部分元素个数
    NSInteger frontCount = midIndex - starIndex + 1;
    
    //后半部分元素的个数
    NSInteger rearCount = endIndex - midIndex;
    
    //把数组拆分成两部分进行归并
    
    //取出前半部分
    NSMutableArray *frontArray = [[NSMutableArray alloc] initWithCapacity:frontCount];
    for (NSInteger i = 0; i < frontCount; i ++) {
        [frontArray addObject:array[starIndex + i]];
    }
    
    //取出后半部分
    NSMutableArray *rearArray = [[NSMutableArray alloc] initWithCapacity:rearCount];
    for (NSInteger i = 0; i < rearCount; i ++) {
        [rearArray addObject:array[midIndex + i + 1]];
    }
    
    
    //进行比较归并
    
    NSInteger fi = 0;
    NSInteger ri = 0;
    NSInteger oi = starIndex;
    
    //当两个子数组中都有元素时才进行合并
    while (fi < frontArray.count && ri < rearArray.count) {
        
        if(frontArray[fi] <= rearArray[ri]){
            
            array[oi++] = frontArray[fi++];
            continue;
        }
        
        array[oi++] = rearArray[ri++];
    }

    //前面元素中经过合并后仍然有元素，把剩余的元素进行添加
    while (fi < frontArray.count) {
        
        array[oi++] = frontArray[fi++];
        
    }

    //后边元素经过合并后仍然有元素，把剩余元素进行添加
    while (ri < rearArray.count) {
        
        array[oi++] = rearArray[ri++];
        
    }
    
    NSLog(@"第%d合并结果如下：", ++ sort_count);
    [self displayArrayWithArray:array];
}

　　　　上面的代码只是进行问题解的合并，下方是对问题进行拆分，分解成规模比较小的子问题，递归分解代码如下，在这就不多说了，下面代码中已经给出了注释。

#pragma mark -- 本方法是把问题进行递归分割，使其成为多个相似的子问题，然后在把子问题进行合
+(void) mergeSortWithArray: (NSMutableArray *)array
             WithStarIndex: (NSInteger) starIndex
              WithEndIndex: (NSInteger) endIndex
{
    //递归结束条件
    if (starIndex >= endIndex) {
        return;
    }
    
    //找出中点进行分解
    NSInteger midIndex = (starIndex + endIndex)/2;
    
    //递归分解前半部分
    [self mergeSortWithArray:array WithStarIndex:starIndex WithEndIndex:midIndex];
    
    //递归分解后半部分
    [self mergeSortWithArray:array WithStarIndex:midIndex + 1 WithEndIndex:endIndex];
    
    //经过上面的递归分解后，最小的子数组里只有一个元素，也就是有序的了，然后从底层进行递归合并
    [self mergeWithArray:array WithStarIndex:starIndex WithMidIndex:midIndex WithEndIndex:endIndex];
    
}

　　

　　调用归并排序代码如下：

        //归并排序
        [Sort mergeSortWithArray:array WithStarIndex:0 WithEndIndex:array.count-1];

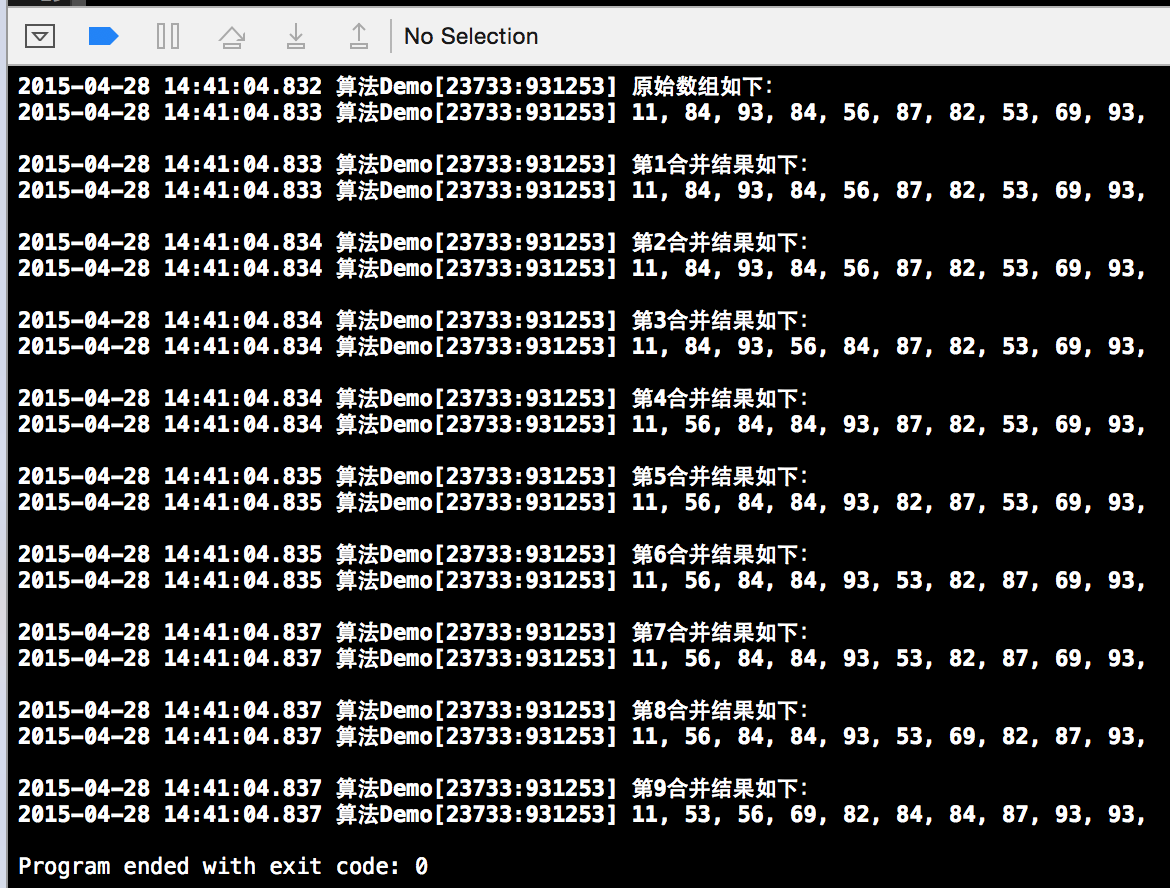
　　运行结果如下，仔细观察每次归并后的结果，你会找到规律的哦。

　　今天的博客就先到这吧，编程是少不了算法的呀，继续努力学习中。