序
-
红黑树主要是对
2-3树进行编码,红黑树背后的基本思想是用标准的二叉查找树(完全由 2- 结点构成)和一些额外的信息(替换 3- 结点)来表示 2-3 树,树中的链接分为两种类型:红链接:将两个 2- 结点连接起来构成一个 3- 结点黑链接:则是2-3树中的普通链接
-
确切的说,我们将 3- 结点表示为由一条左斜的红色链接(两个2-结点其中之一是另一个的左子结点)相连的两个2-结点。这中表示法的优点是:我们无需修改就可以直接使用标准的二叉查找树的get方法

红黑树定义
- 红黑树是含有红黑链接并满足下列条件的 二叉查找树 :
- 红链接均为左链接
- 没有任何一个结点同时和两条红链接相连
- 该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑色链接数量相同
- 红黑树与2-3树对应关系
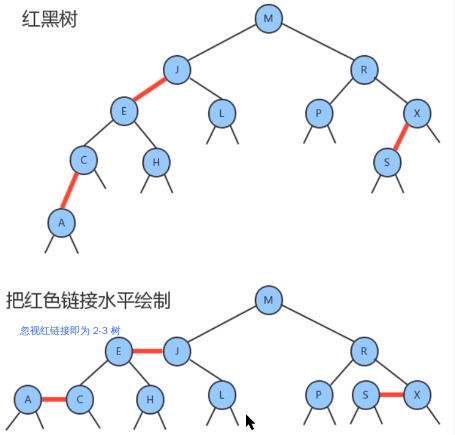
API设计
| 类名 | Node<Key,Value> |
|---|---|
| 构造方法 | Node(Key key,Value value,Node left,Node right, boolean color):创建 Node 对象 |
| 1. public Node left:记录左子结点 | |
| 2. public Node right:记录右子结点 | |
| 成员变量 | 3. public Key key:存储键 |
| 4. public Value value:存储值 | |
| 5. public boolean color:由其父结点指向它的链接的颜色,红色为true |
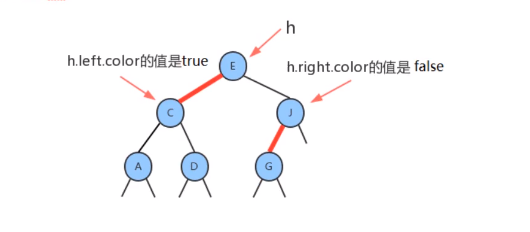
注意: 红线关系,父结点指向子结点的线为红色,代表子结点的color 是RED,属性为true。即父结点与子结点间线的颜色实际上是子节点的颜色
平衡化
- 在对红黑树进行一些增删改查的操作后,很有可能会出现
红色的右链接或者两条连续红色的链接,而这些都不满足红黑树的定义,所以我们需要对这些情况通过旋转进行修复,让红黑树保持平衡
左旋
-
当某个结点的左子结点为黑色,右子结点为红色,此时需要左旋
-
前提:结点x(值为S),结点h(值为E)
- h.right = x.left;x.left = h。x以轴心和为轴逆时针旋转后,轴心h变为了x的左结点
- x.color = h.color
- h.color=true,让h的color属性变为RED,因为旋转后,h的父结点指向h的链为红色

右旋
- 当某个结点的左子结点为红色,且左子节点的左子节点也是红色,需要右旋
- 前提:结点x(值为E),结点h(值为s)
- 让x的右子结点成为h的左子结点:h.left=x.right
- 让h成为x的右子结点:x.right=h
- 让x的color变为h的color属性值:x.color=h.color(注:h.color==false 黑色)
- 让h的color为RED
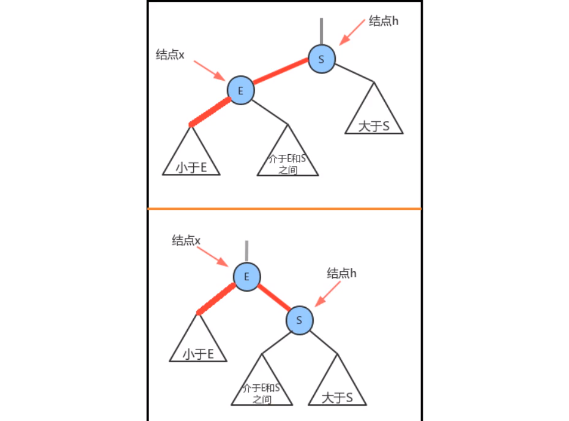
- 右旋转结束后发现,右旋后依然不满足红黑树定义。虽然 x(值为E) 与 h(值为S)节点不是左链为连续的两条红色的线,但是 x 节点(值为E)的右链又为红色了。
后续会通过颜色反转解决当前问题,现在右旋已经结束
红黑树的插入
向单个2-结点中插入新键
- 一棵只含有一个键的红黑树只含有一个2-结点。插入另一个键后,我们马上就需要将他们旋转
-
如果新键小于当前结点的键,我们只需要增加一个红色结点即可,新的红黑树和单个3-结点完全等价
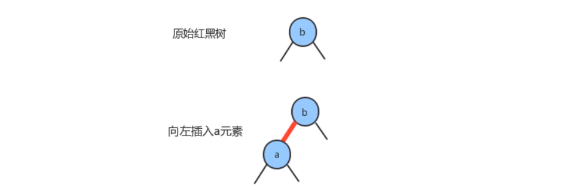
-
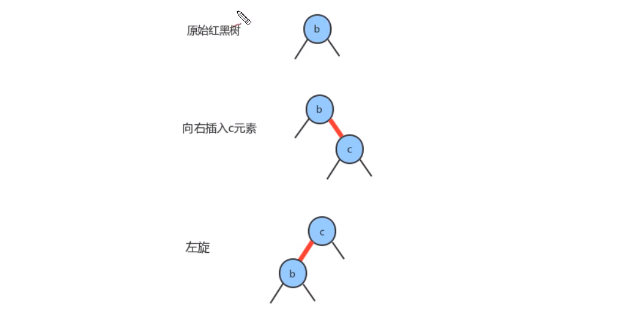
如果
新键大于当前结点的键,那么新增的红色结点将会产生一条红色的右链接,此时我们需要通过左旋,把红色右链接变成左链接,插入操作才算完成。形成的新的红黑树依然和3-结点等价,其中含有两个键,一条红色的链接
-
向底部的2-结点插入新键
- 用和二叉查找树相同的方式向一棵红黑树中插入一个新键,会在树的底部新增一个结点(可以保证有序性),唯一的区别地方是我们会用红链接将新结点和它的父结点想连。如果它的父结点是一个
2-结点,那么刚才讨论两种方式仍然适用
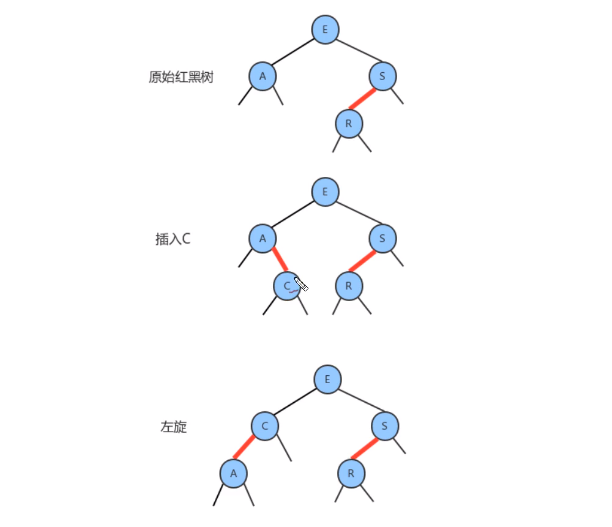
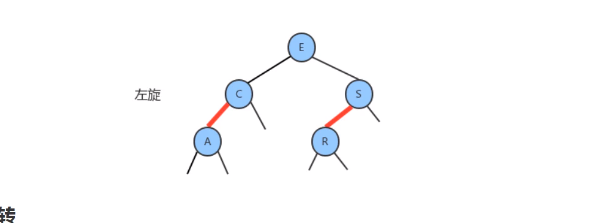
颜色反转
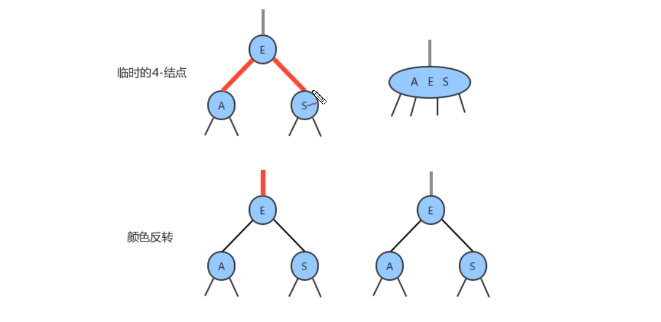
- 当一个结点的左子结点和右子结点的color都为RED时,也是是出现了
临时的4-结点此时只需要把左子结点和右子结点的颜色变为BLACK,同时让当前的结点的颜色变为RED即可
向一棵双键树(即一个3-结点)中插入新键
- 可分为三种子情况
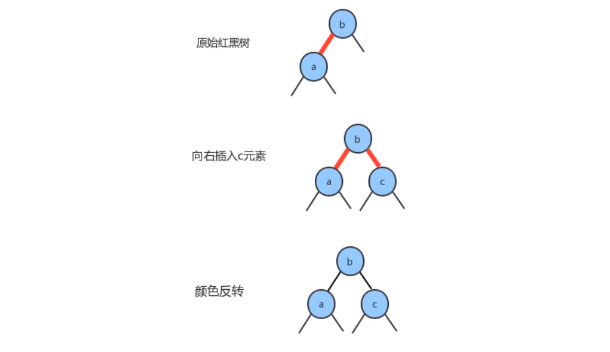
- 新键大于原树中的两个键
- 新结点置于右子结点
- 颜色反转(子结点color为black,父结点color为RED)
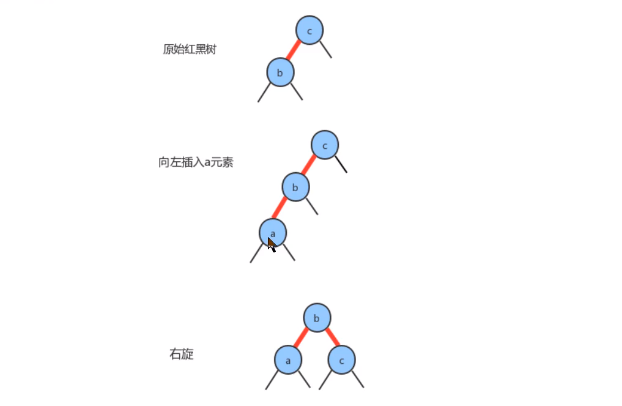
- 新键小于原树中的两个键
- 新结点置于左子结点
- 以原始父结点为轴右旋
- 颜色反转(子结点color为black,父结点color为RED)
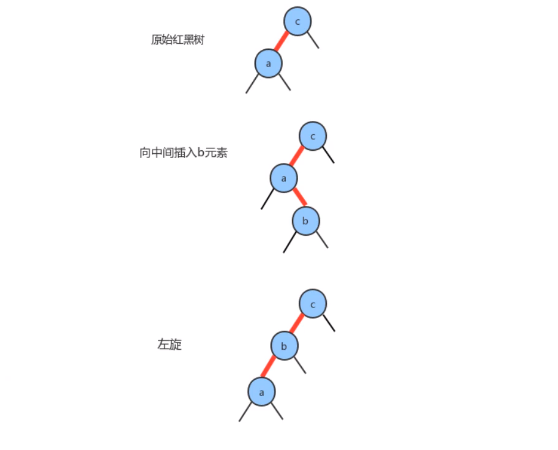
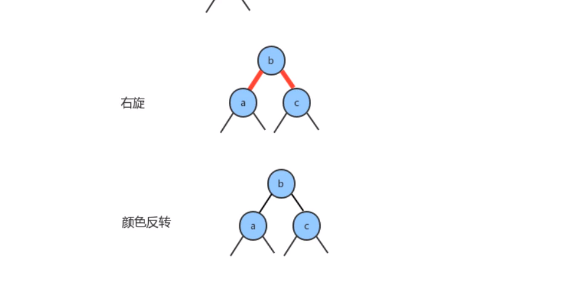
- 新键介于原数中两个键之间
- 新结点置于左子结点的右子结点
- 以左子结点为轴
左旋 - 以父结点为轴
右旋 - 颜色反转(子结点color为black,父结点color为RED)
向树底部的3-结点插入新键
-
假设在树底部的一个
3-结点下加入一个新的结点。之前的3种情况都会出现。颜色转换会使中间
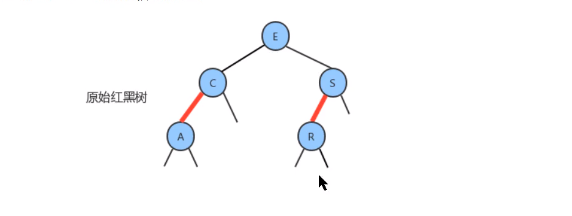
- 指向新结点的链接可能是
3-结点的右链接,此时只需转换颜色即可 - 指向新结点的链接可能是
3-结点的左链接,此时需要先进行右旋转(以父结点为轴),然后再颜色转换,然后左旋(根结点为轴)
- 指向新结点的链接可能是
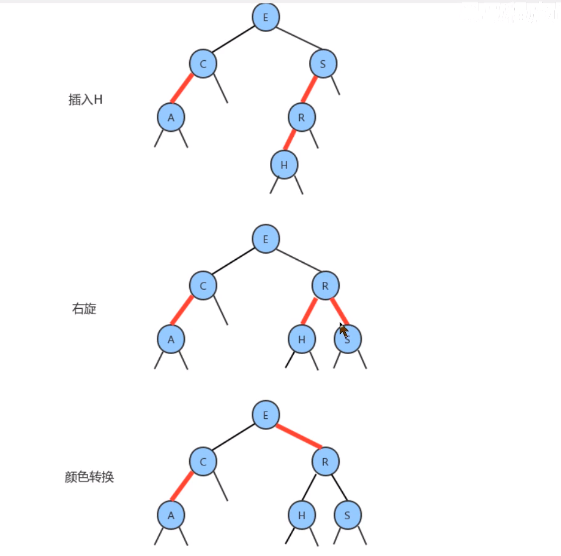
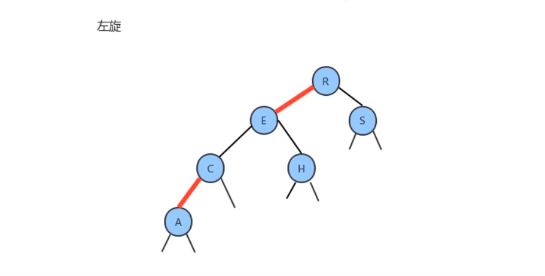
- 指向新结点的链接可能是`3-结的中链接` 此时`需要先左旋转,然后右旋转,最后转换颜色`
红黑树的API设计
| - | - |
|---|---|
| 类名 | RedBlackTree<Key extends Comparable |
| 构造方法 | RedBlackTree():创建RedBlackTree对象 |
| 1.private boolean isRed(Node x):判断当前结点的父指向链接是否为红色 | |
| 2.private Node rotateLeft(Node h):左旋调整 | |
| 3.private Node rotateRight(Node h):右旋调整 | |
| 4.private void flipColors(Node h):颜色反转,相当于完成拆分4-结点 | |
| 成员方法 | 5.public void put(Key key,Value val):在树上完成插入操作 |
| 6.private Node put(Node h,Key key,Value val):在指定树中,完成插入操作,并返回添加元素后新的树 | |
| 7.public Value get(Key key):根据key,从树中找出对应的值 | |
| 8.private Value get(Node x,Key key):从指定的树x中,找出key对应的值 | |
| 9.public int size():获取树中元素的个数 | |
| 1.private Node root:记录根结点 | |
| 成员变量 | 2.private int N:记录树中元素的个数 |
| 3.private static final boolean RED:红色标识链接 | |
| 4.private static final boolean BLACK:黑色标识链接 |
红黑树实现
向树插入结点
- 判断当前树是否为空
- 比较新结点和树上的结点的键和新节点的键的大小
- 新节点key小于树上的结点的key,向左放置(递归)
- 新节点key大于树上的结点的key,向右放置(递归)
- 新结点key等于树上的结点的key,值替换
- 左旋
- 右旋
- 颜色反转
规律
- 红黑树中所有的结点都是
2-结点,每插入一个新结点,我们都期望把它和它的父结点组成一个3-结点,因此,新插入的结点都是红色结点,当不满足红黑树定义时才进行旋转或颜色反转
红黑树API实现
public class RedBlackTree<Key extends Comparable<Key>,Value> {
//根节点
private Node root;
//元素个数
private int N;
//红色链接
private static final boolean RED=true;
//黑色链接
private static final boolean BLACK=false;
//结点类
private class Node{
public Key key;
private Value value;
public Node left;
public Node right;
public boolean color;
public Node(Key key, Value value, Node left, Node right, boolean color) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
this.color = color;
}
}
//获取树中元素的个数
public int size(){
return N;
}
//当前结点的color是否为RED
public boolean isRed(Node x){
if (x == null) {
return false;
}
return x.color==RED;
}
//左旋转
public Node rotateLeft(Node h){
//获取h结点的右子结点,标记为x
Node x = h.right;
//将 x结点的左子结点 赋值给 h节点的右子节点
h.right = x.left;
//让 h结点成为 x结点的 右子节点
x.left = h;
//将h结点的颜色(黑色) 赋值给 x结点
x.color = h.color;
//将h结点的颜色转换为 红色
h.color = RED;
//左旋后,父链接指向x结点,所以返回x
return x;
}
//右旋转
public Node rotateRight(Node h) {
//获取h结点的左子结点,标记为x
Node x = h.left;
//将 x结点的右子节点 赋值给 h结点的左子节点
h.left = x.right;
//将 h结点 赋值给 x结点的右子节点
x.right = h;
//将 h结点的颜色 赋值 给 x结点
x.color = h.color;
//将 h结点的颜色 设置为 红色
h.color = RED;
//右旋后,父链接志向x结点,所以返回x
return x;
}
//颜色反转,完成拆分 4- 结点
public void flipColors(Node h) {
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
//在整个树上完成插入操作
public void put(Key key,Value val){
root = put(root, key, val);
root.color = RED;
}
//指定结点插入 结点
public Node put(Node h,Key key,Value val){
//判断树是否为空,如果为空则直接返回一个红色的结点就可以了
if (h == null) {
N++;
return new Node(key, val, null, null, RED);
}
//比较新结点key 和 插入位置的结点的key 大小
int cmp = key.compareTo(h.key);
if (cmp < 0) {
//新结点往左放
h.left=put(h.left,key,val);
}
if (cmp > 0) {
//新结点往右放
h.right=put(h.right,key,val);
}
if (cmp == 0) {
h.value=val;
}
//左旋,当 当前左子结点为黑色,当前右子结点为红色,需要反转
if (isRed(h.right) && !isRed(h.left)) {
//旋转后,返回的结果应该 指向 当前树
h=rotateLeft(h);
}
//右旋:当当前结点的左子结点 和 当前结点的左子结点的左子结点 都为红色
if (isRed(h.left) && isRed(h.left.left)) {
//旋转后,返回的结果应该 指向 当前树
h=rotateRight(h);
}
//颜色转换:当 当前结点的左子结点 和 右子结点都为红色,需要进行颜色反转
if (isRed(h.left) && isRed(h.right)) {
flipColors(h);
}
//当前 子树h 添加了 新结点 成功后,返回 h 子树
return h;
}
public Value get(Key key) {
return get(root, key);
}
public Value get(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) {
return get(x.left, key);
} else if (cmp > 0) {
return get(x.right, key);
} else {
return x.value;
}
}
}
- 学自Bilibili黑马