鲁棒学习
最小二乘法易受异常值影响
异常值处理:
- 提前剔除异常值再训练
- 提高异常值的鲁棒性--鲁棒学习算法
1. (L_1)损失最小化

第(r_i)个样本的残差:

L2损失随残差呈平方级增长:
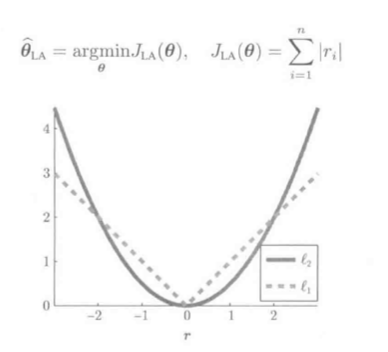
L1损失最小化学习较最小绝对值偏差学习(hat heta_{LA})
L1损失LS受异常值影响较小:
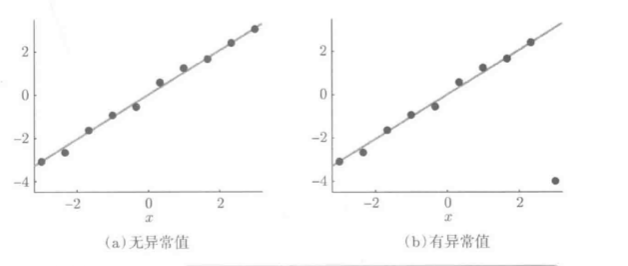
L2损失LS输出结果是训练样本输出值的均值:

L1损失LS输出结果是训练样本输出值的中间值:

对于L1损失LS, 只要中间值不变, 异常值对最终结果影响不大.
2.Huber损失最小化
Huber损失LS能很好地平衡有效性和鲁棒性.
Huber混合使用了L1和L2损失:
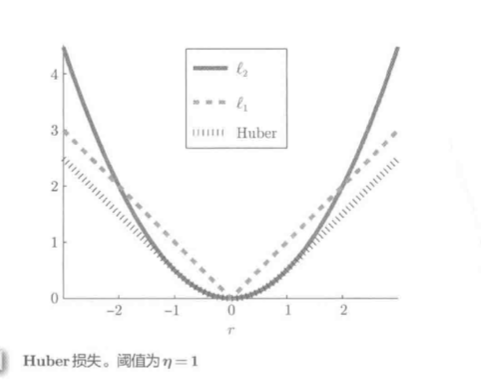
公式:
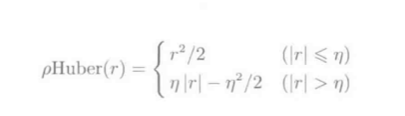
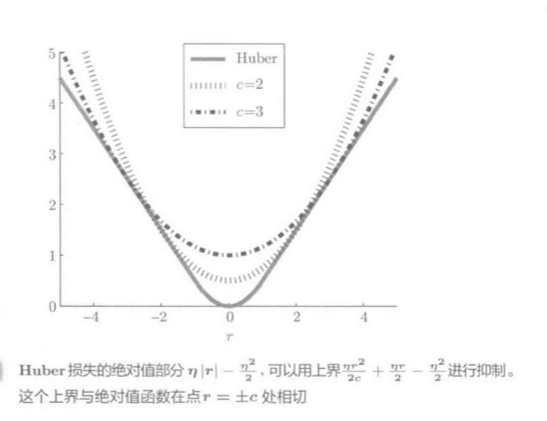
- r为残差的绝对值. (|r|)小于阈值(eta)(正常值), 则为L2损失, 否则(异常值), 为L1损失
- 为了和L2损失平滑连接, 省去了(frac{eta^2}{2})
最终的Huber损失LS:
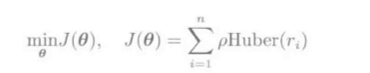
应用到线性模型:
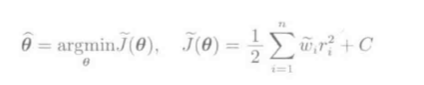
图示:
权重$ ilde{w}_i$定义:

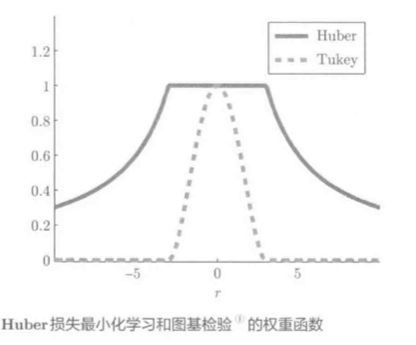
Huber LS和Tukey损失权重函数对比:
加权最小二乘学习法的解:

反复加权最小二乘学习:

对线性模型禁行Huber LS学习(阈值(eta=1)):
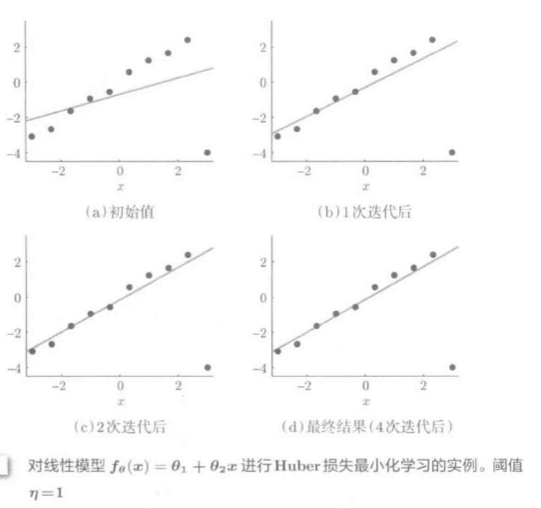
(eta)非常小是, Huber LS是L1损失的平滑近似, 故可通过反复加权最小二乘法对L1损失近似求解.
3.Tukey损失最小化
同Huber, 是对L1和L2损失优化组合, 平衡有效性和鲁棒性的学习方法.
Tukey损失:

公式:

- 残差绝对值(|r|)大于(eta)(异常值)时, 以(frac{eta^3}{6})的形式输出, 具有非常高的鲁棒性
- Tukey损失不是凸函数, 有多个局部最优解, 不易求得全局最优解
- 通过反复加权LS求局部最优解
权重函数:
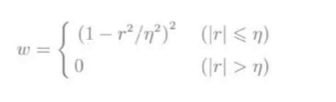
(|r| > eta) 时, 权重变为0, 故Tukey损失LS完全不受显著异常值影响
Tukey损失最小化学习举例:
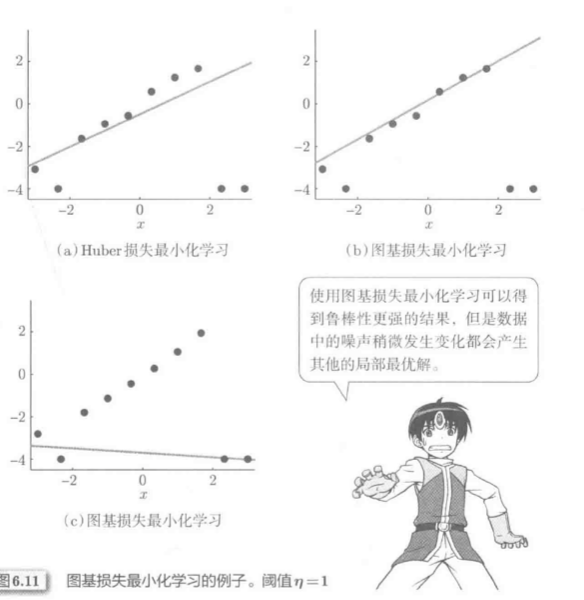
4.(L_1)约束的Huber损失
约束条件:

- L1约束LS: 通过L2约束的LS反复迭代求得
- Huber损失最小化: 加权LS反复迭代求得
- 上述两者都是最小二乘法(LS)反复迭代, 通过二者优化组合, 可得L1约束的Huber损失最小化算法
以高斯核模型:
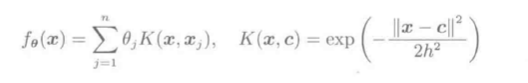
为例, 下面展示了L1约束Huber损失最小化迭代求解过程:

高斯核模型L1约束的Huber损失最小化学习举例:

- L2损失LS数值上不稳定, 在矩阵KWK对角中加入(10^{-6})以稳定
- L2损失LS, 无论是否有L1约束, 都易受(x=0)附近异常值影响
- Huber损失LS中, 无论是否有L1约束,均可很好地抑制异常值影响
- L2损失LS和Huber损失LS中50个参数全部非0
- L1约束的L2损失LS的50个参数有38个为0; L1约束的Huber损失LS的50个参数中有36个为0