郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18)
Abstract
在本文中,我们利用二值神经网络(BNN)的效率来学习具有离散因子状态和动作空间的规划域的复杂状态转换模型。为了直接利用这种转换结构进行规划,我们提出了两个基于布尔可满足性(FDSATPlan)和二值线性规划(FD-BLP-Plan)减少的BNN学习因子规划问题的新编码。通过实验,我们展示了使用BNN学习复杂转换模型的有效性,并测试了两种编码在学到的因子规划问题上的运行时效率。在初步调查之后,我们提出了一种基于广义地标约束的增量约束生成算法,以提高我们编码的规划精度。最后,我们展示了如何将最佳性能编码(FD-BLP-Plan+)扩展到目标之外,以处理带有奖励的因子规划问题。
1 Introduction
深度神经网络显著提高了自主系统执行复杂任务的能力,例如图像识别[Krizhevsky et al., 2012]、语音识别[Deng et al., 2013]和自然语言处理[Collobert et al., 2011],并且可以在围棋[Silver et al., 2016]和国际象棋[Silver et al., 2017]等复杂的规划任务中胜过人类和人类设计的超人类系统。
在学习和在线规划领域,最近关于HD-MILP-Plan [Say et al., 2017]的工作探索了一个两阶段框架,该框架 (i) 使用基于ReLU的深度网络从数据中学习转换模型,以及 (ii) 使用混合整数线性规划对学习的转换模型进行最佳规划,但没有提供能够学习和规划离散状态变量的编码。作为基于ReLU的深度网络的替代方案,二值神经网络(BNN)[Hubara et al., 2016]已被引入,具有在离散变量上学习紧凑模型的特定能力,为转换学习和我们在本文中探索的离散因子状态和动作空间规划提供了新的形式[Boutilier et al., 1999]。然而,使用这些BNN转换模型进行规划提出了两个重要的问题:(i) 在具有因子状态和(并发)动作空间的域中规划的BNN最有效的编码是什么? (ii) 鉴于BNN可能学习不正确的域模型,规划器如何修复BNN编码以提高其规划准确性?
为了回答问题 (i),我们提出了两个基于布尔可满足性(FD-SAT-Plan)和二值线性规划(FD-BLP-Plan)简化的BNN学习因子规划问题的新编码。在具有多个大小和范围设置的三个因子规划域中,我们测试了使用BNN学习复杂状态转换模型的有效性,并测试了两种编码在学习的因子规划问题上的运行时效率。虽然有一些方法可以从数据中学习PDDL模型[Yang et al., 2007; Amir and Chang, 2008]和优秀的PDDL规划者[Helmert, 2006; Richter and Westphal, 2010],我们注意到BNN比基于PDDL的学习范式更具有表现力,用于学习可能依赖于一个或多个动作的联合执行的因子动作空间中的并发效果。此外,虽然蒙特卡洛树搜索(MCTS)方法[Kocsis and Szepesvári, 2006; Keller and Helmert, 2013]包括AlphaGo [Silver et al., 2016]和AlphaGoZero [Silver et al., 2016]可以在技术上使用BNN学习的转换动力学黑盒模型进行规划,与这项工作不同,他们无法利用BNN转换结构,他们将无法提供关于学习模型的最优性保证。
为了回答问题 (ii),我们引入了一种基于基于分解的成本最优经典规划器[Davies et al., 2015]的广义地标约束的增量算法,其中在在线规划期间,我们检测并约束来自规划者的决策空间,有效提高规划精度。最后,在上述 (i) 和 (ii) 的答案的基础上,我们扩展了性能最佳的编码,以处理具有一般奖励的因子规划问题(FD-BLP-Plan+)。
总之,这项工作提供了第一个能够在具有混合(连续和离散)因子状态和动作空间作为BNN的域中学习复杂转换模型的规划器,并能够在可满足性(或优化)编码中利用它们的结构来进行规划。实证结果表明,在学习和原始领域的目标导向和奖励导向规划方面都有很强的表现,并为数据驱动的基于模型的规划社区提供了一种新的转换学习和规划形式。
2 Preliminaries
在我们介绍学习规划问题的SAT和BLP编码之前,我们回顾了推动这项工作的初步准备工作。
2.1 Problem Definition

2.2 Factored Planning with Deep-Net Learned Transition Models

2.3 Binarized Neural Networks
二值神经网络(BNN)是具有二值权重和激活函数的神经网络[Hubara et al., 2016]。在推理过程中,BNN通过将大多数算术运算替换为按位运算来减少系统的内存需求。BNN层按以下顺序堆叠:

2.4 Boolean Satisfiability Problem
布尔可满足性问题(SAT)是确定是否存在对布尔公式的变量赋值的问题,使得该公式的计算结果为真(即可满足)[Davis and Putnam, 1960]。虽然SAT的理论最坏情况复杂度是NP-Complete,但最先进的SAT求解器在实验上可以很好地扩展到具有数百万个变量和约束的大型实例[Biere et al., 2009]。
Boolean Cardinality Constraints


2.5 Binary Linear Programming Problem
二元线性规划(BLP)问题需要找到具有线性约束、线性目标函数和二值决策变量的数学模型变量的最优值分配。与SAT类似,BLP的理论最坏情况复杂度是NP-Complete。最先进的BLP求解器[IBM, 2017]利用分支定界算法,可以在其编码大小上有效地处理基数约束。
2.6 Generalized Landmark Constraints

3 SAT Compilation of the Learned Factored Planning Problem
在本节中,我们展示了如何使用BNN将学习到的因子规划问题减少到SAT中,我们将其称为因子深度SAT规划器(FD-SAT-Plan)。
3.1 Propositional Variables
首先,我们描述了FD-SAT-Plan中使用的命题变量集。我们使用三组命题变量:动作变量、状态变量和BNN二值单元,其中变量使用按位编码。

3.2 Parameters
接下来我们定义FD-SATPlan中使用的额外参数。

3.3 The SAT Compilation
下面,我们用BNN定义学到的因子规划问题![]() 的SAT编码。
的SAT编码。
Initial and Goal State Constraints
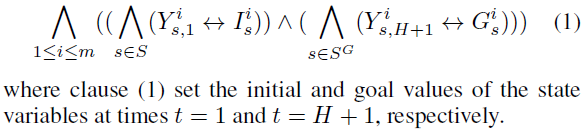
BNN Constraints


Global Constraints

4 BLP Compilation of the Learned Factored Planning Problem
给定FD-SAT-Plan,我们使用BNN呈现学习的因子规划问题![]() 的BLP编码,我们将其称为因子深度BLP规划器(FD-BLP-Plan)。
的BLP编码,我们将其称为因子深度BLP规划器(FD-BLP-Plan)。
4.1 Binary Variables and Parameters
FD-BLP-Plan使用与FD-SAT-Plan相同的决策变量和参数集。
4.2 The BLP Compilation


5 Incremental Factored Planning Algorithm for FD-SAT-Plan and FD-BLP-Plan

6 Experimental Results
6.1 Domain Descriptions
6.2 Transition Learning Performance
6.3 Planning Performance on the Learned Factored Planning Problems
6.4 Planning Performance on the Factored Planning Problems
6.5 Planning Performance on the Factored Planning Problems with Reward Specifications
7 Conclusion