郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Neurocomputing, (2019): 39-47
Abstract
训练脉冲神经网络(SNN)的问题是理解大脑内计算的必要先决条件，这一领域仍处于起步阶段。以前的工作表明，多层SNN中的监督学习使仿生网络能够通过分层特征获取来识别刺激模式。尽管梯度下降在多层(深度)SNN中显示出令人印象深刻的性能，但通常认为它在生物学上不合理，而且计算成本也很高。本文提出了一种新的监督学习方法，该方法基于嵌入在IF神经元网络中的基于事件的脉冲时序依赖可塑性(STDP)规则。所提出的时间局部学习规则遵循在每个时间步骤应用的反向传播权重变化更新。这种方法具有精确梯度下降和时间局部高效STDP的优点。因此，这种方法能够解决一些关于大脑中发生的准确和有效计算的开放性问题。XOR问题、Iris数据和MNIST数据集的实验结果表明，所提出的SNN与传统NN一样成功。我们的方法也与最先进的多层SNN相媲美。
Keywords: Spiking neural networks, STDP, Supervised learning, Temporally local learning, Multi-layer SNN.
1. Introduction
在神经网络研究的脉络中，脉冲神经网络(SNN)因其生物学上看似合理的真实性、理论计算能力和能源效率而引起了近期和长期的兴趣[1, 2, 3, 4, 5]。SNN中的神经元(类似于大脑中的生物神经元)通过离散的脉冲事件进行通信。实现脉冲框架的一个重要问题是这些网络如何在监督下训练，而没有连续值的可微激活函数？多层监督学习是SNN中的一个关键概念，用于证明其预测和分类刺激模式的能力。
SNN中最早的监督学习SpikeProp是由Bohte et al. (2002) [6]提出的，开发了一种基于梯度下降的学习方法，类似于嵌入在多层神经网络中的传统反向传播。SpikeProp通过将脉冲时间作为神经元膜电位的函数来最小化单个所需脉冲和输出脉冲之间的距离。后来，Quick-Prop和RProp [7]被引入作为SpikeProp的更快版本。遵循相同的方法，Booij et al. (2005) [8]和Ghosh et al. (2009) [9]提出了新的SpikeProp算法，最小化多个期望和输出脉冲之间的距离，以提高模型响应时间模式的编码能力。梯度下降(GD)作为一种流行的监督学习方法，仍然被用于在脉冲平台中以离线[10]或在线[11]方式开发高性能监督学习。Chronotron [12]利用Victor & Purpura (VP)度量[13]进行E-learning(离线)和突触电流模拟用于I-learning(在线)是SNN中GD的另一个示例。正如在Chronotron中实现的那样，GD中的误差函数可以通过突触后和突触前电流(或膜电位)[14](在线)或脉冲序列距离度量(离线)之间的差异度量来定义，例如von Rossum距离[15, 16]和脉冲序列的内积[17]。在线梯度下降法最近也引起了对深度SNN的兴趣[18, 19]。尽管在线GD方法已经成功地在多层SNN中开发监督学习，但使用基于膜电位和导数的方法在生物学上是不可信的，因为SNN仅通过离散的脉冲事件进行通信。此外，对于多层SNN，GD的计算成本很高。最近，Xie et al. (2016) [20]开发了一种归一化的脉冲反向传播，计算突触后脉冲时间(仍然需要昂贵的计算)，而不是每个时间步的膜电位，以提高算法的效率。
另一种研究方法利用修改后的Widrow-Hoff学习规则用于SNN。例如，ReSuMe [21]引入了单层监督学习方法；后来，Sporea et al. (2013) [22]使用反向传播将其扩展到多层框架。SPAN [23, 24]还通过将离散脉冲转换为相应的模拟信号来使用Widrow-Hoff。上面提到的学习方法比基于GD的方法更有效但不太准确。另一种有效的监督学习方法属于基于感知器的方法，例如Tempotron [25]，其中每个脉冲事件都被视为训练感知器的二值标签[26, 27]。这些模型呈现单层监督学习。然而，spike/no-spike分类的想法拓宽了一个新的监督学习类别，结合了有效的脉冲时序依赖可塑性(STDP) [28, 29, 30]和根据神经元标签触发的anti-STDP [31, 32]。STDP是一种生物学上看似合理的学习规则，发生在大脑中，其中突触前脉冲发生在当前突触后脉冲加强互连突触(LTP)之前；否则，突触被削弱(LTD)。
在本文中，我们提出了新颖的多层监督学习规则来训练IF神经元的SNN。所提出的方法利用了高效的仿生STDP和高性能反向传播(梯度下降)规则。首先，我们证明了IF神经元近似于整流线性单元(ReLU)。然后，我们开发了一种时间局部学习方法，该方法由STDP/anti-STDP规则指定，该规则源自可以在每个时间步骤应用的反向传播权重变化规则。
2. Method
在提出基于脉冲的时间局部学习规则之前，我们展示了生物IF神经元如何逼近配备有整流线性单元(ReLU)激活函数的众所周知的人工神经元。这种近似是将基于发放率的学习转换为时空局部学习的第一步。
2.1. Rectified Linear Unit versus IF neuron
具有整流线性单元(ReLU)激活函数f(y)的神经元通过相应的突触权重wh接收输入信号xh定义如下：
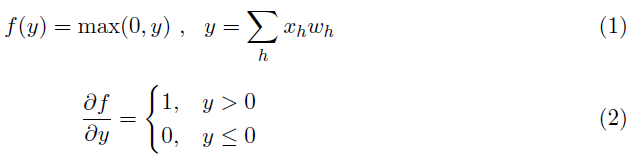
定理：IF神经元逼近ReLU神经元。具体来说，IF神经元的膜电位近似于ReLU神经元的激活值。
证明：非泄漏IF神经元整合由其输入脉冲序列产生的时间膜电位，当其膜电位U(t)达到神经元的阈值时发放，IF神经元的简化公式如公式3所示：
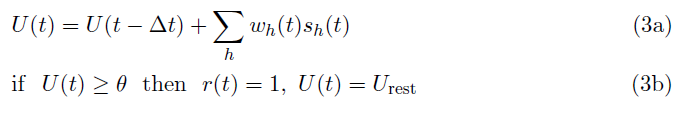
其中，sh(t)和r(t)分别是时间 t (sh(t), r(t) ∈ {0, 1})的突触前和突触后脉冲。神经元的膜电位在发放时重置为静息电位Urest(假设Urest = 0)。通过将突触前脉冲序列Gh(t)公式化为delta Dirac函数(公式4)的总和，公式1中的输入值xh ∈ [0, 1]，可以通过在脉冲时间间隔 T 上积分来确定，如公式5所示。
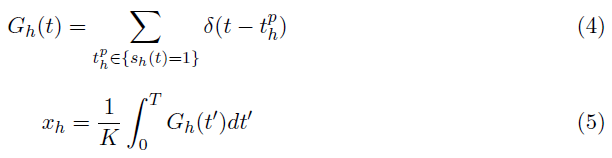
其中 K 是一个常数，表示T ms间隔内的最大脉冲数。
在连续突触后脉冲r(t - α)和r(t)之间的短时间段(t - α, t]：
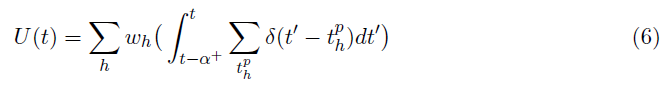
上面计算的膜电位(U(t))大于阈值θ (U(t) ≥ θ)。因此，当我们假设IF神经元是非泄漏的并且其膜电位在发放时重置为零时，R 突触后脉冲需要累积的膜电位(公式7)。累积的膜电位Utot是通过对公式6中计算的亚膜电位的线性求和获得的。根据这个定义，突触后脉冲计数 R 表示通过非线性、基于阈值的激活函数传递的输出值
。
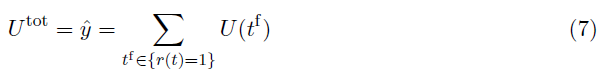
其中Utot以T ms指定IF神经元的活动，这与突触后脉冲计数 R 成比例相关。因此，IF神经元的激活函数可以被表示为：
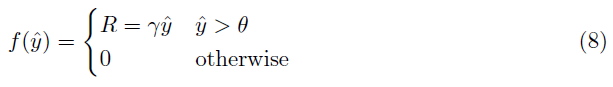
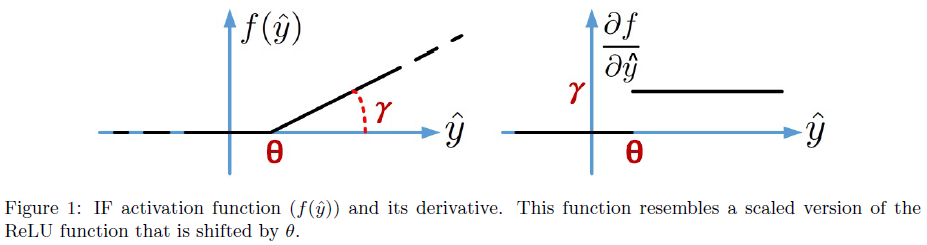
其中，γ ∝ T · θ-1是控制突触后脉冲计数的常数。这个激活函数类似于一个线性缩放的ReLU函数，它向右移动了θ。图1显示了激活函数及其导数。
该定理为从传统学习规则(应用于ReLU神经元)派生的新的基于脉冲的学习规则(应用于脉冲IF神经元)打开了一扇新的大门。具体来说，在下一节中，我们使用这个定理来提出一个应用于脉冲IF神经元的基于STDP的反向传播规则。
2.2. Backpropagation using STDP
所提出的学习规则的灵感来自于为配备ReLU激活函数的神经网络报告的反向传播更新规则。图2显示了用于描述本文中传统和脉冲神经网络的网络架构和参数。这两个网络之间的主要区别在于它们的数据通信，其中神经网络(左)接收并生成实数，而SNN(右)在T ms时间间隔内接收并生成脉冲序列。
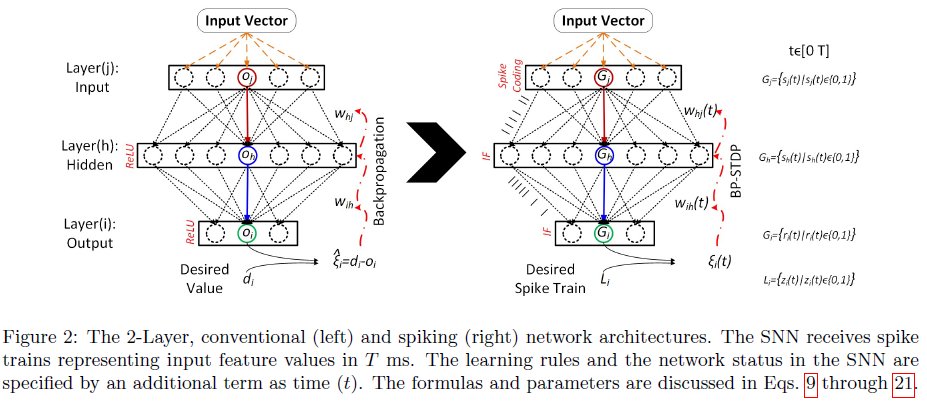
配备梯度下降(GD)的非脉冲神经网络解决了一个优化问题，其中期望值 d 和输出值 o 之间的平方差被最小化[33, 34]。为接收 N 个训练样本的 M 个输出神经元计算的公共目标函数如公式9所示。
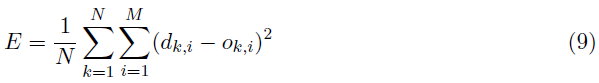
线性输出神经元的权重变化公式(使用GD，学习率为μ)，比如说 i，接收 H 个输入，oh，(对于单个训练样本)是通过以下方式实现的：
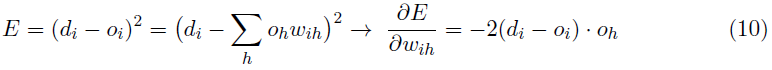
通过反转导数上的符号，我们有：
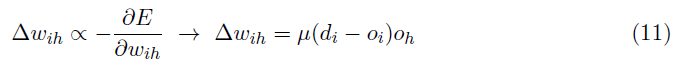
通过假设di, oi, oh, 因为脉冲序列的脉冲计数Li, Gi和Gh [35](参见公式4和12)，分别可以重新表示上面定义的权重变化，以便计算SNN中的突触权重更新。这个假设在将脉冲IF神经元近似为ReLU神经元时是有效的(定理1)。公式13显示了T = 50 ms后的更新规则。
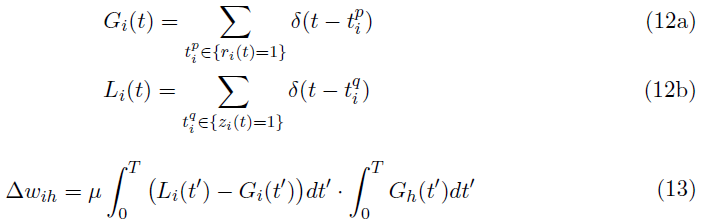
然而，公式13中的权重变化规则在时间上不是局部的。为了使学习规则在时间上局部化，我们将时间间隔 T 分解为子间隔，使得每个子间隔包含零或一个脉冲。因此，学习规则，在公式13的短时间内由公式14指定。
为了实现上述公式，可以使用基于事件的STDP和anti-STDP的组合。所提出的学习规则使用教师信号更新突触权重以在STDP和anti-STDP之间切换。也就是说，目标神经元经历STDP，非目标神经元经历anti-STDP。所需的脉冲序列 z 是根据输入的标签定义的。因此，目标神经元由具有最大脉冲频率(β)的脉冲序列表示，非目标神经元是沉默的。此外，学习规则在所需的脉冲时间zi(t)触发(对于所有目标神经元，所需的脉冲时间相同)。公式15显示了应用于我们的监督SNN的输出层的权重变化。
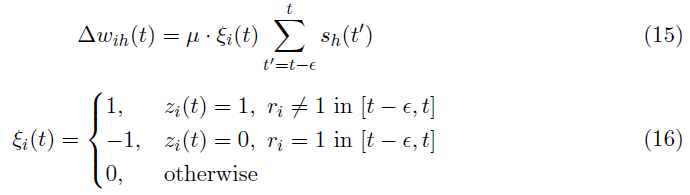
然后，输出层的突触权重更新为：
目标神经元由zi(t)确定，其中zi(t) = 1表示目标神经元，zi(t) = 0表示非目标神经元。输出层的权重变化场景从所需的脉冲时间开始。在期望的脉冲时间 t 处，目标神经元应该在很短的时间间隔[t - ε, t]内(被称为STDP窗口)发放。否则，在相同的时间间隔内，突触权重会随着突触前活动(大多为0或1 个脉冲)成比例增加。突触前活动由
表示，它计算[t - ε, t]间隔中的突触前脉冲。另一方面，发放时的非目标神经元以同样的方式经历权重下降。这个场景的灵感来自于传统的GD，同时支持SNN中的时空局部学习。
上面写的学习规则适用于由监督训练的单层SNN。为了训练多层SNN，我们使用受传统反向传播规则启发的相同想法。应用于ReLU神经元隐藏层的反向传播权重变化规则如公式18所示。
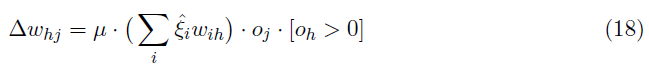
其中，
表示期望值和输出值之间的差异(di - oi)。在我们的SNN中，
由ξi近似(公式16)。值[oh > 0]指定隐藏层中ReLU神经元的导数。使用IF神经元对ReLU神经元的近似(公式8)，类似于输出层(公式13)，权重变化公式可以用多层SNN中的脉冲计数重新表示，如公式19所示。
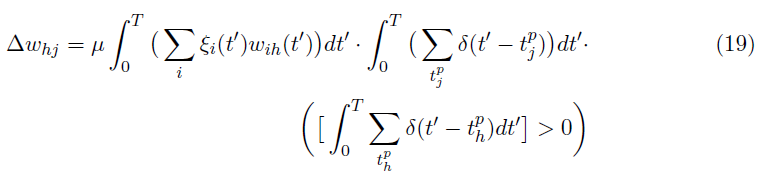
将 T 划分为短子间隔[t - ε, t]，用于更新隐藏突触权重的时间局部规则公式如下。
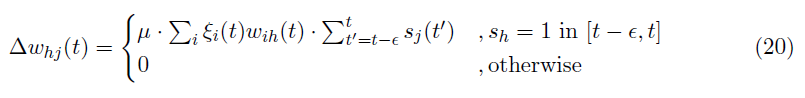
最后，隐藏层的突触权重被更新为：
当隐藏神经元 h 发放(突触后脉冲发生)时，上述学习规则可以是非零的。因此，权重根据突触前(sj(t))和突触后(sh(t))脉冲时间更新，类似于标准STDP规则。此外，ReLU的导数(oh > 0)类似于IF神经元中的脉冲生成(参见公式20中的条件)。按照这种时空突触权重变化规则的场景，我们可以构建一个配备基于STDP的反向传播算法的多层SNN，称为BP-STDP。图3演示了应用于具有一个隐藏层的SNN的BP-STDP算法。
3. Results
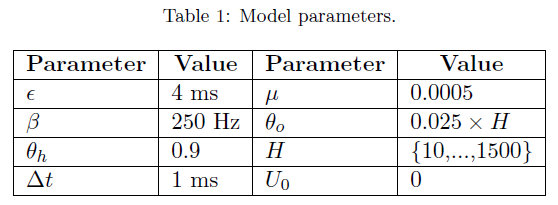
我们进行了三个不同的实验来评估所提出的模型(BP-STDP)关于XOR问题、iris数据集[36]和MNIST数据集[37]。实验设置中使用的参数如表1所示。所有实验的突触权重均由具有零均值和单位标准差的高斯随机数初始化。
3.1. XOR problem
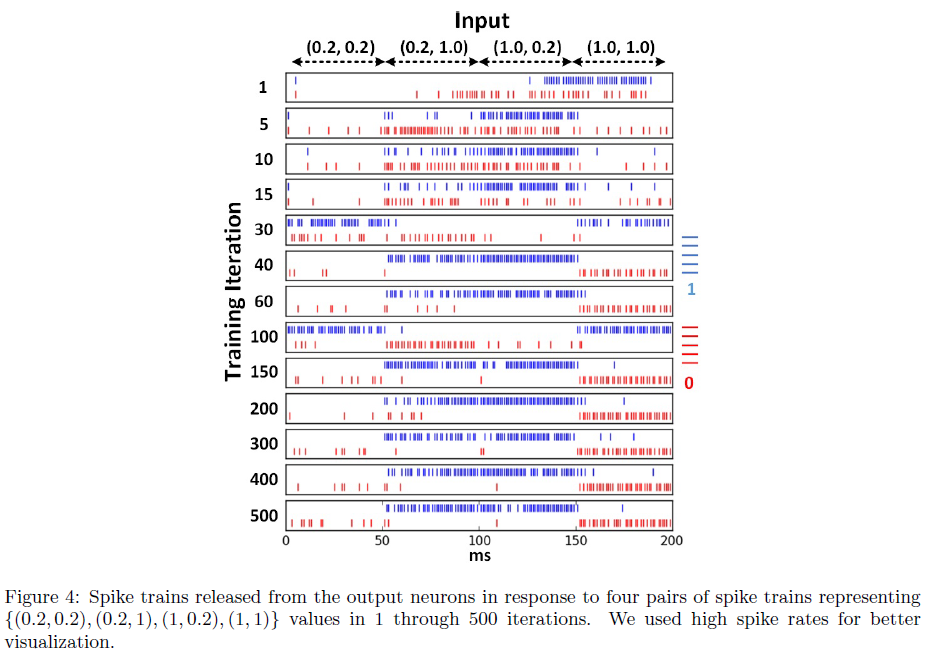
BP-STDP算法通过XOR问题进行评估，以显示其解决线性不可分的能力。数据集包含四个数据点{(0.2, 0.2), (0.2, 1), (1, 0.2), (1, 1)}和对应的标签{0, 1, 1, 0}。我们使用0.2而不是0来激活IF神经元(以释放脉冲)。网络架构由2个输入、20个隐藏和2个输出IF神经元组成。这个问题的隐藏神经元的数量对结果几乎没有影响。我们将研究隐藏神经元数量对MNIST分类任务的影响。每个输入神经元释放对应于输入值的脉冲序列，使得值1由具有最大脉冲发放率(250 Hz)的脉冲序列表示。
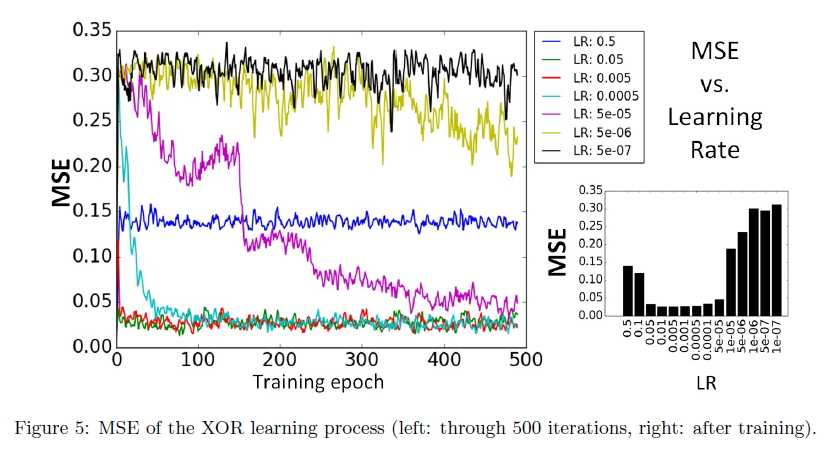
图4显示了训练过程，其中每个框代表两个输出神经元相对于确定{0, 1, 1, 0}类的四个输入脉冲模式的活动。经过大约150次训练迭代后，输出神经元对输入类别具有选择性。图5展示了使用公式22中定义的能量函数的学习收敛过程。该图表明正确的学习率μ，落在[0.01, 0.0005]范围内。
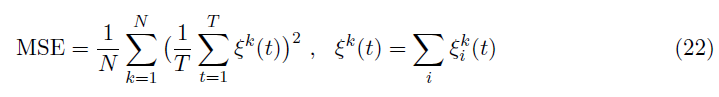
在公式22中，N和
表示训练批大小和输出神经元 i 响应样本 k 的误差值。
3.2. Iris dataset
Iris数据集由三种不同类型的花朵(Setosa, Versicolour, and Virginica)组成，由花瓣和萼片的长度和宽度(4个特征)表示。在对[0, 1]范围内的特征值进行归一化后，会生成输入脉冲序列。本实验中的网络架构由4个输入、30个隐藏和3个输出IF神经元组成。我们在初步实验中发现，使用超过10个隐藏神经元并不能显著提高准确性。
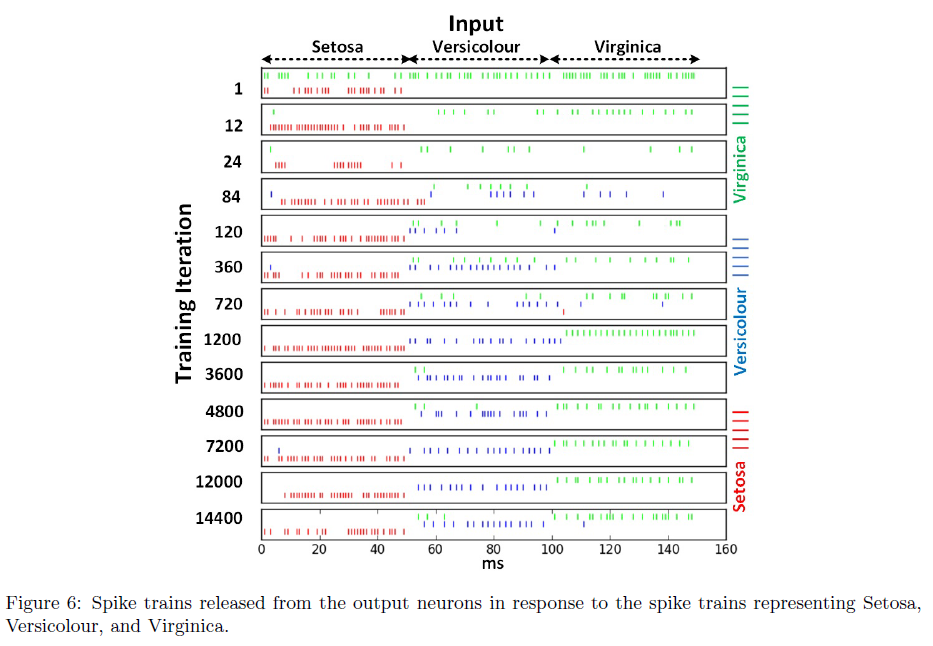
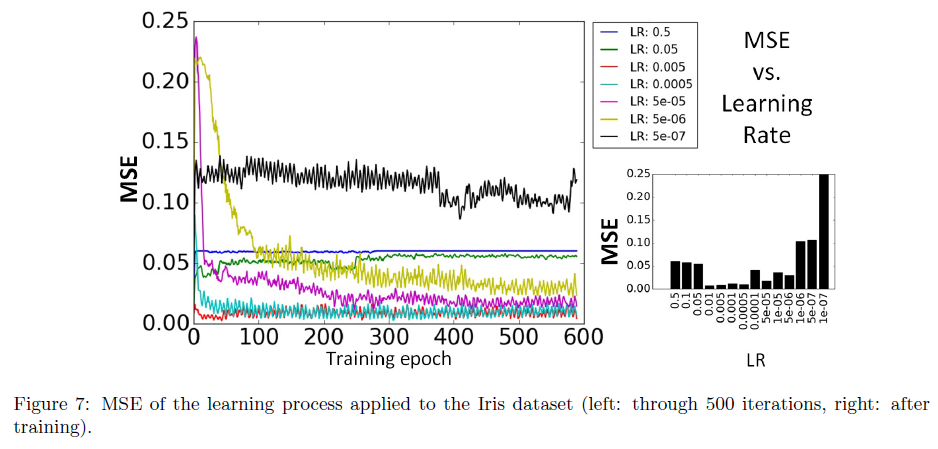
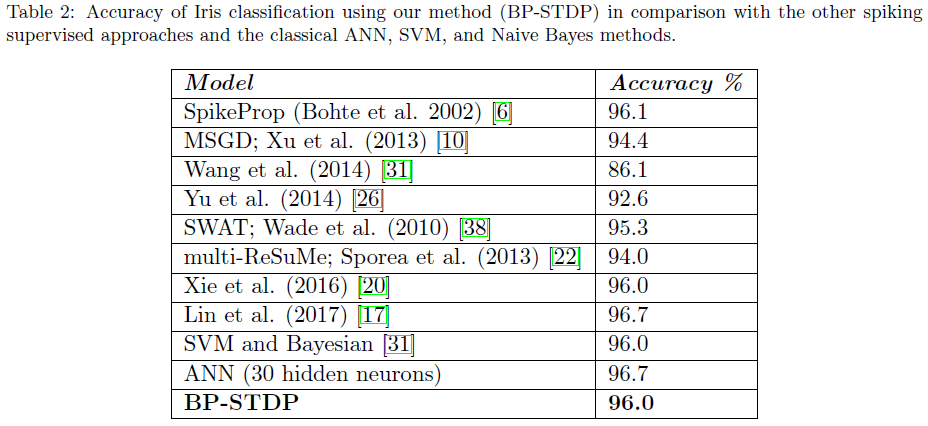
与XOR问题获得的结果类似，图6说明SNN通过训练收敛到对三种花朵模式具有选择性。图7显示了SNN根据公式22中定义的MSE的学习过程。使用5折交叉验证的最终评估报告准确率为96%，而配备标准反向传播的传统神经网络准确率为96.7%。该结果表明所提出的BP-STDP算法在训练时间SNN方面是成功的。此外，表2将我们的结果与其他基于脉冲的和传统的监督学习方法进行了比较。我们的模型优于(或同等执行)以前的多脉冲监督学习算法，除了Lin等人的方法[17]，其中开发了一种时空且计算量大的GD。
3.3. MNIST Dataset
为了评估所提出的算法在解决更复杂问题方面的效果，我们评估了MNIST上的SNN，该SNN具有784个输入、100到1500个隐藏和10个输出IF神经元，配备BP-STDP。SNN在60k训练和10k测试样本上进行了训练和测试。输入脉冲序列由随机滞后生成，脉冲发放率与[0, 1]范围内的归一化像素值成比例。
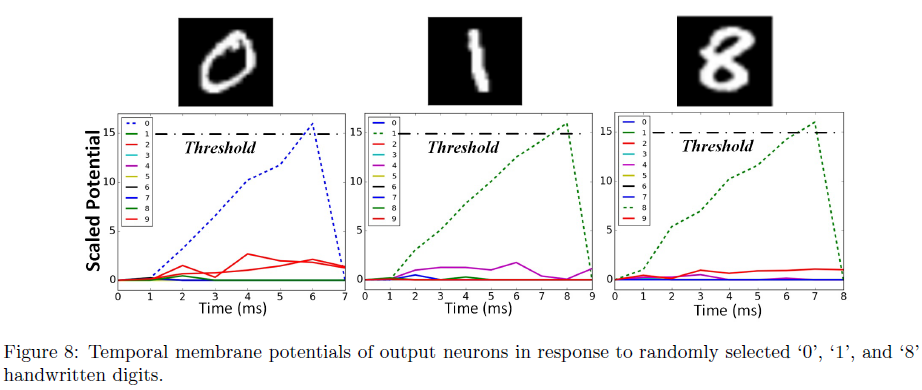
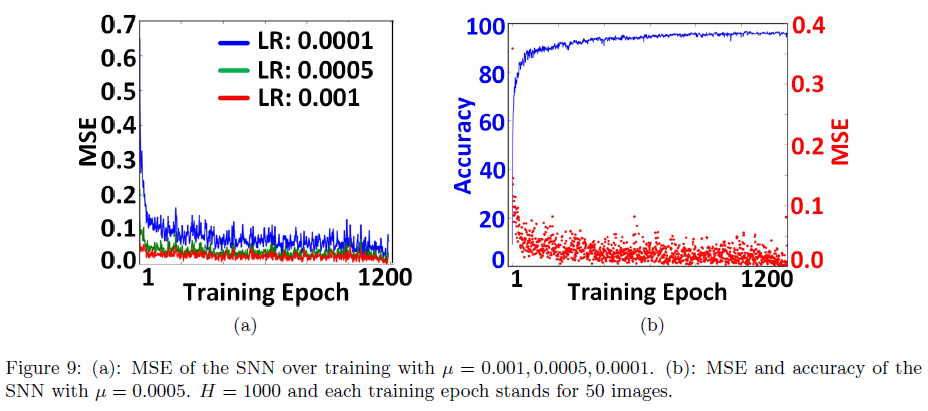
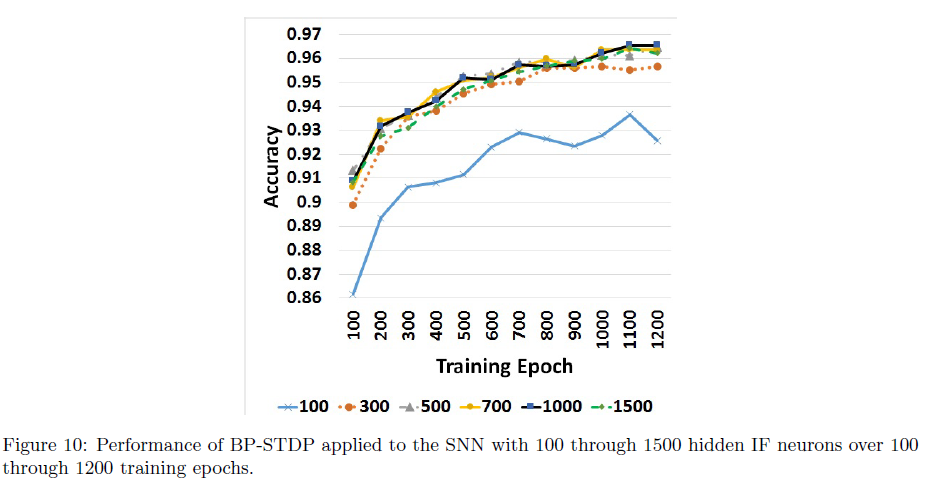
图8显示了输出神经元的膜电位(训练后)，以响应从三个随机选择的数字生成的脉冲序列。目标神经元的膜电位快速增长并达到阈值，而其他神经元的活动接近于零。此外，这种快速响应(< 9 ms)减少了网络的响应延迟。图9a显示了1200个训练epoch的学习过程。每个epoch代表50个MNIST数字。该图中的MSE轨迹显示了BP-STDP在0.001和0.0005的学习率下的快速收敛。图9b显示了在训练中具有1000个隐藏神经元的SNN的MSE值和准确率。在100和900个训练epoch之后，分别达到了90%和96%的性能。为了检查隐藏神经元数量对性能的影响，我们将BP-STDP规则应用于具有100到1500个隐藏IF神经元的六个SNN。图10显示了这些SNN的训练准确率。最佳准确率属于具有超过500个隐藏神经元的网络。
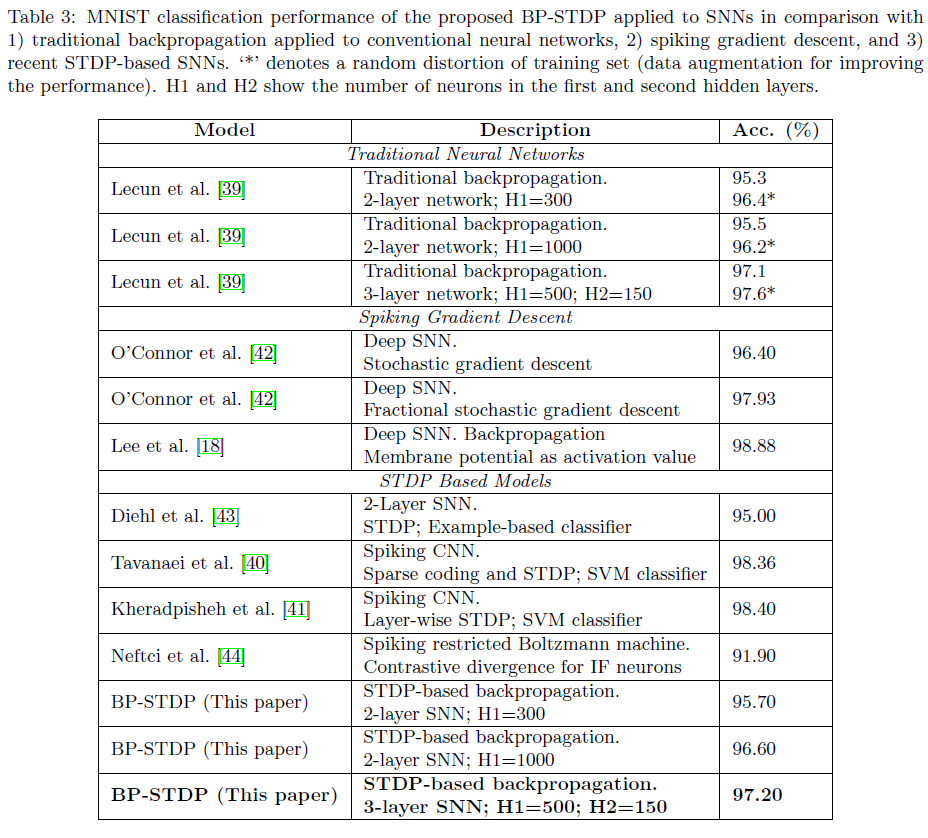
最后，BP-STDP算法在2层和3层SNN上进行了评估。SNN架构(隐藏神经元的数量)与[39]中使用的神经网络架构相同，以显示更好的比较。我们的模型在2层和3层SNN上分别实现了96.6±0.1%和97.2±0.07%的准确率。这些结果与传统神经网络(通过反向传播训练)[39]报告的准确率相当。表3将所提出的监督学习方法(BP-STDP)与传统的反向传播算法(或GD)、嵌入多层(深度)SNN中的脉冲反向传播方法以及最近用于MNIST分类的基于STDP的SNN进行了比较。这种比较证实了应用于时间SNN架构的仿生BP-STDP规则的成功。我们的模型是唯一适用于多层SNN的高性能、基于端到端STDP的监督学习方法。[40, 41]中介绍的SNN开发了用于特征提取的多层STDP学习。然而，他们使用支持向量机(SVM)分类器作为最终监督层。尽管梯度下降方法成功执行[42, 43, 18]，但它们并没有在SNN中提供受生物启发的高效STDP学习。具体来说，最近开发的使用反向传播的深度SNN [18]显示出比BP-STDP的更高的精度；然而，它计算的是由神经元的膜电位获得的激活函数的导数，而不是使用它们的脉冲事件。
4. Discussion
BP-STDP为SNN引入了一种新颖的监督学习。它显示出与最先进的传统梯度下降方法相当的有希望的性能。BP-STDP提供了受生物启发的局部学习规则，该规则考虑了脉冲时间以及后续IF神经元层中的脉冲发放率。Bengio et al. [45]表明突触权重变化与突触前脉冲事件和突触后时间活动成正比，类似于STDP规则，并证实了Hinton的想法，即STDP可以与突触后时间率相关[46]。在本文中，我们展示了反向传播更新规则可用于开发时空局部学习规则，该规则在SNN中实现生物学上合理的STDP。
所提出的算法的灵感来自于用于传统ReLU神经元网络的反向传播更新规则。然而，它在SNN中开发了生物学合理的、暂时的局部学习规则。这个问题是通过IF神经元与ReLU神经元的初始近似来完成的，以支持SNN中基于脉冲的通信方案。脉冲监督学习规则将STDP和anti-STDP组合应用于对应于时间突触前和突触后神经活动的脉冲神经层。因此，我们在脉冲框架中利用了准确的梯度下降和有效的时间局部STDP。主要问题是误差传播如何与多层网络架构中IF神经元的脉冲行为相对应？为了回答这个问题，让我们假设误差值是一个信号，它要么刺激(
)要么抑制(
)IF神经元发放。刺激(抑制)神经元是指增加(减少)其膜电位，该膜电位由其输入权重和突触前脉冲事件按比例控制。因此，随着BP-STDP更新规则根据误差信号和突触前脉冲时间在时间上改变突触权重，它在每个时间步操纵隐藏层的神经活动(动作电位)。
实验结果表明BP-STDP在实现嵌入多层SNN的监督学习方面取得了成功。XOR问题证明了BP-STDP在T ms时间间隔内对由脉冲序列表示的非线性可分样本进行分类的能力。IRIS和MNIST分类的复杂问题展示了与传统反向传播算法和最近的SNN相当的性能(分别为96.0%和97.2%)，而BP-STDP为脉冲模式分类提供了一种基于STDP的端到端监督学习。使用仿生和时间局部STDP规则引导我们更接近大脑中发生的有效计算。据我们所知，这种方法是第一个高性能的基于STDP的监督学习，同时避免了计算成本高的梯度下降。
5. Conclusion
本文表明，如果神经元的活动映射到脉冲发放率，则IF神经元近似于整流线性单元(ReLU)。因此，脉冲IF神经元网络可以进行应用于传统神经网络的反向传播学习。我们提出了一种时间局部学习规则(源自传统的反向传播更新)，将STDP和anti-STDP规则结合在IF神经元的多层SNN中。该模型(BP-STDP)利用了脉冲平台中受生物启发的有效的STDP规则和GD的力量来训练多层网络。此外，将基于GD的权重变化规则转换为基于脉冲的STDP规则比开发脉冲GD规则更容易且计算成本更低。XOR问题的实验表明，所提出的SNN可以对非线性可分模式进行分类。此外，对Iris和MNIST数据集的最终评估表明，其分类精度可与传统神经元和脉冲神经元的最新多层网络相媲美。
BP-STDP模型的有希望的结果保证了我们未来的研究，以开发配备BP-STDP和正则化模块的深度SNN。深度SNN可用于更大的模式识别任务，同时保留高效的类脑计算。