Q学习方法失败的方式和原因

Q学习方法只能通过训练Q_θ以满足自洽方程，间接优化智能体性能。这种学习有很多失败模式，所以它往往不太稳定。

有关Q学习方法失败的方式和原因的更多信息，请参见下面材料：

1）Tsitsiklis and van Roy的这篇经典论文：

2）Szepesvari的评论(见第4.3.2节)：

　　Q学习对具有参数形式(Q_θ; θ ∈ R^d)的函数近似的明显扩展是： 

(当λ = 0时，将其与(21)进行比较)。算法13显示了对应于使用线性函数近似方法的情况的伪代码，即当Q_θ = θ^Tφ，其中。

　　尽管上述更新规则在实践中被广泛使用，但其收敛性却鲜为人知。事实上，由于TD(0)是该算法的一个特例(当每个状态只有一个动作时)，就像TD(0)一样，这个更新规则在使用异策采样或非线性函数近似时也会收敛失败(参见第3.2.1节)。唯一已知的收敛结果归因于Melo et al. (2008)证明了在样本分布相当严格的条件下收敛。最近，沿着最近的类似梯度的TD算法，Maei et al. (2010b)提出了贪婪梯度Q学习(greedy GQ)算法，它解除了以前的限制条件：这种新算法保证独立于采样分布而收敛。然而，由于该算法推导中使用的目标函数是非凸的，即使使用线性函数近似，该算法也可能陷入局部最小值。

State aggregation 由于上述更新规则可能无法收敛，因此自然会限制所采用的价值函数近似方法和/或根据需要修改更新过程。本着这种精神，让我们首先考虑Q_θ是状态(和动作)聚合器的情况(参见第3.2节)。然后，如果((X_t, A_t); t ≥ 0)是平稳的，那么该算法的行为将与适当定义的"induced MDP"中的表格式Q学习完全一样。因此它将收敛到最优动作-价值函数Q*的某个近似值(Bertsekas and Tsitsiklis, 1996, 第6.7.7节)。

Soft state aggregation 聚合的一个不良特性是价值函数在底层区域的边界处不会是平滑的。Singh et al. (1995)提出通过"软化"版本的Q学习来解决这个问题。在他们的算法中，近似的动作-价值函数具有线性平均器的形式：，其中si(x, a) ≥ 0 (i=1, ... , d)且。修改更新规则使得在任何时候，只更新参数向量θ_t的一个分量。要更新的分量是通过从带参数的多项分布(s₁(X_t, A_t), ... , s_d(X_t, A_t))中随机抽取索引I_t ∈ {1, ... , d}选择的。

Interpolation-based Q-learning Szepesvári and Smart (2004)提出了对该算法的修改，他们称之为基于插值的Q学习(IBQ学习)。IBQ同时更新参数向量的所有分量，从而减少更新的方差。IBQ学习也可以看作是Q学习与状态和动作聚合一起使用到插值器的泛化(Tsitsiklis and Van Roy, 1996, 第8节讨论了在已知模型的拟合值迭代的上下文中的插值器)。这个想法是将参数向量的每个分量 i 视为某个"代表性"状态-动作对的价值估计。即 , (Q_θ; θ ∈ R^d)的选择使得Q_θ(x_i, a_i) = θ_i适用于所有i = 1, ... , d。这使得Q_θ成为插值器(解释算法的名称)。接下来，选择相似性函数。例如，可以使用s_i(x, a) = exp(-c₁d₁(x, x_i)² - c₂d₂(a, a_i)²)，其中c₁, c₂ > 0且d₁, d₂是适当的"距离"函数。IBQ学习的更新规则如下：

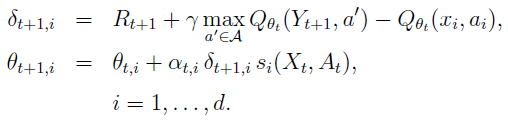
　　每个组件都根据它对未来总奖励的预测程度以及其关联的状态-动作对与刚刚访问的状态-动作对的相似度进行更新。如果相似度较小，则误差δ_t+1,i对分量变化的影响也较小。该算法使用局部步长序列(α_t,i; t ≥ 0)，即每个分量都有一个步长。

　　Szepesvári and Smart (2004)证明该算法几乎肯定收敛，只要 (i) 函数类Q_θ满足上述插值属性和映射θ → Q_θ是非展开式(即，对于任何θ, θ' ∈ R^d成立)；(ii) 局部步长序列(αt,i; t ≥ 0)被适当地选择并且 (iii) 状态-动作空间的所有区域都被((X_t, A_t); t ≥ 0)"足够的访问"。它们还提供了所学动作-价值函数质量的误差界限。分析的核心是，由于θ → Q_θ是非展开式，算法实现了价值迭代的增量近似版本，底层算子是收缩。这是因为在收缩之后应用的非扩展或在非扩展之后应用的收缩是收缩。使用非展开式的想法首先出现在Gordon (1995)和Tsitsiklis and Van Roy (1996)研究拟合价值迭代的研究中。

Fitted Q-iteration 拟合Q迭代使用动作-价值函数实现拟合价值迭代。鉴于先前的迭代Q_t，其想法是在选定的状态-动作对处形成(T*Q_t)(x, a)的蒙特卡罗近似，然后使用自己喜欢的回归方法对结果点进行回归。算法14显示了该方法的伪代码。众所周知，除非使用特殊的回归量，否则拟合Q迭代可能会发散(Baird, 1995; Boyan and Moore, 1995; Tsitsiklis and Van Roy, 1996)。Ormoneit and Sen (2002)建议使用核平均，而Ernst et al. (2005)建议使用基于树的回归器。这些保证收敛(例如，如果在每次迭代中将相同的数据输入算法)，因为它们实现了局部平均以及Gordon (1995)的结果；Tsitsiklis and Van Roy (1996)适用于它们。Riedmiller (2005)报告了神经网络的良好经验结果，至少当通过遵循关于最新迭代的策略贪婪获得的新观察被增量添加到更新中使用的样本集时。如果没有好的初始策略可用，那么样本的改变是必不可少的，即，当在初始样本中经常被"好"策略访问的状态被低估时(Van Roy (2006)给出了为什么这很重要的理论论据)在状态聚合的上下文中)。

　　Antos et al. (2007)和Munos and Szepesvári (2008)证明了适用于一大类回归方法的有限样本性能界限，这些回归方法在候选动作-价值函数的固定空间 F 上使用经验风险最小化。它们的界限取决于 F 的最坏情况贝尔曼误差：

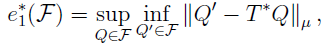
其中 μ 是训练样本中状态-动作对的分布。也就是说，衡量 F 与的接近程度。导出的边界具有监督学习中存在的有限样本边界的形式(参见公式33)，除了近似误差由测量。注意，在前面提到的拟合价值迭代收敛的反例中，，这表明导致发散的原因是函数近似方法缺乏灵活性。

3）Sutton and Barto的第11章，尤其是第11.3节(关于函数近似、自举(bootstrapping)和异策数据的"致命三元组"，共同导致价值学习算法的不稳定性)：

　　只要我们的方法同时满足下述三个基本要素，就一定会有不稳定和发散的危险。我们称这三个基本要素为致命三要素。

• 函数逼近：函数逼近是一种强大且可拓展的方法，可将我们的函数泛化到一个远大于内存和计算资源限制的状态空间中(如线性函数逼近和人工神经网络)。
• 自举法：使用当前的目标估计值进行更新以得到新的目标估计值(如动态规划和TD方法)，而不是只依赖于真实收益和完整回报(如蒙特卡洛方法)。
• 离轨策略训练：用来进行训练的状态转移分布不是由目标策略产生的。如动态规划中所作的，遍历整个状态空间并均匀地更新所有状态而不理会目标策略就是一个离轨策略训练的例子。