郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Proceedings of the 38th International Conference on Machine Learning, PMLR 139, 2021.
Abstract
灾难性干扰，即在学习新信息时丢失先前学到的信息，仍然是机器学习的主要挑战。由于生物体似乎不会受到这个问题的困扰，研究人员从生物学中汲取灵感，以提高人工智能系统的记忆力。然而，之前使用仿生机制的尝试通常导致系统在训练期间依赖任务边界信息和/或推理期间的显式任务识别，这些信息在现实世界中是不可用的。在这里，我们展示了神经启发的机制，如突触巩固和元可塑性，可以减轻脉冲神经网络中的灾难性干扰，仅使用突触局部信息，不需要任务意识，并且具有固定的内存大小，不需要在新任务训练时增加。我们的模型TACOS将神经调节与复杂的突触动力学相结合，在保护先前信息的同时实现新的学习。我们在序列图像识别任务上评估TACOS，并证明其在减少灾难性干扰方面的有效性。我们的结果表明TACOS在领域增量学习场景中优于现有的正则化技术。我们还报告了消融研究的结果，以分别阐明每种神经启发机制的贡献。
1. Introduction
当人工神经网络面临新的学习任务时，它们很容易忘记以前获得的材料。这个被称为灾难性干扰(或灾难性遗忘)的问题于1989年首次被发现(McCloskey & Cohen，1989)，并且一直是人工智能领域的一个挑战(Parisi et al., 2019)。相比之下，人类和其他哺乳动物似乎没有这个问题。因此，神经科学家和机器学习研究人员试图了解生物神经系统如何能够避免灾难性干扰，并且已经提出了几种解释，其中大多数是化生性的变化(Abraham & Bear, 1996; Finnie & Nader, 2012)、神经发生(Parisi et al., 2018)，或回合式回放(McClelland et al., 1995; Robins, 1995; French et al., 2001)。尽管很难获得此类假设的直接证据，但计算模型已经证明，类似的机制可以减少人工神经网络中的灾难性干扰。(Meeter & Murre, 2005; O'Reilly et al., 2011; Draelos et al., 2017)。
在本文中，我们介绍了TACOS，这是一种处理持续学习的脉冲神经网络(SNN)。任务的序列学习是通过误差驱动的神经调节实现的。为了减轻灾难性遗忘，我们提出了一种复杂的突触模型，该模型利用了一种具有突触巩固和异突触衰减的活动依赖性元可塑性。
为什么是脉冲模型？脉冲神经网络被认为比基于发放率的网络在神经上更合理(Pfeiffer & Pfeil, 2018)，并且能量效率高几个数量级(Neftci et al., 2017; Nawrocki et al., 2016)，但至少在计算上与是基于发放率的网络一样强大(Gerstner & Kistler, 2002)。然而，与基于发放率的网络不同，SNN尚未达到适合实际应用的性能水平，主要是因为缺乏高效和可扩展的学习算法。然而，随着新SNN学习算法的引入，这种情况开始发生变化，包括智能体梯度反向传播(Neftci et al., 2019)、三因素赫布学习(Frémaux & Gerstner, 2016)以及稳态或非赫布可塑性(Watt & Desai, 2010)。因此，我们发现自己正处于脉冲神经网络出现的时刻，解决脉冲域中的持续学习问题是前进道路上的重要一步。最近对这项工作的贡献包括对局部赫布学习(Muñoz-Martín et al., 2019)、权重衰减的赫布学习(Panda et al., 2017)以及控制遗忘的好处的调查，这是一种将可塑性导向网络中最不活跃的区域(Allred & Roy, 2020)。然而，这些技术仅限于无法进行监督训练或只能训练单层的脉冲模型。TACOS不受这些限制，并且也不同于之前发布的模型(Kirkpatrick et al., 2017; Chaudhry et al., 2018; Kolouri et al., 2020; Lee et al., 2017; Zenke et al., 2017)因为它在训练或推理期间不需要任何任务识别信息，学习规则完全是突触局部的，并且该算法可扩展到多层脉冲网络。
我们的结果表明，TACOS在领域增量场景中优于几种最先进的正则化模型(van de Ven & Tolias, 2019)。重要的是，TACOS使用少量添加的参数实现了这些结果，使用不依赖于要学习的任务数量的固定内存大小。
除了将TACOS与其他模型进行比较之外，我们还通过以下几点分析TACOS在持续学习中的性能 i) 研究模型在训练数据量减少时的表现，ii) 研究稳定性和可塑性之间的权衡如何依赖关于元可塑性的程度，以及 iii) 进行消融研究以分别研究元可塑性和巩固的影响。
2. Background
2.1. Neural Mechanisms
神经科学家们几乎一致同意，大脑以突触的强度存储记忆(Langille & Brown, 2018)。突触随时间减弱或增强的能力称为突触可塑性，并且已经发现了许多可塑性的细胞机制(Kandel et al., 2014)。其中，长时程增强(LTP) (Nicoll, 2017)是研究最多的一种，它被认为是学习和记忆的主要细胞机制(Frankland & Bontempi, 2005; Kandel et al., 2014)。早期LTP (E-LTP)由中等强度刺激产生，持续数分钟到数小时(Abraham, 2003; Malenka & Bear, 2004)；晚期LTP (L-LTP)需要更强烈的刺激，可以持续数周、数月甚至数年(Abraham et al., 2002)。从E-LTP到L-LTP的转变被称为突触巩固，它与短期记忆转变为长期记忆有关(Sossin, 2008; Morris, 2003)。
表征巩固的记忆寿命的增加(自发衰减率降低)伴随着对记忆破坏和修改(Dudai)的抵抗力增加，对应于突触水平的可塑性降低(Richards ＆ Frankland, 2017)，一种元可塑性形式("突触可塑性的可塑性") (Abraham & Bear, 1996)。这两种转变——降低衰减率和降低对破坏的敏感性——都是记忆稳定性的重要方面。
另一个对学习和记忆很重要的生理过程是神经调节。与点对点突触传递不同，神经调节可以通过广泛释放神经递质来响应新奇、惊喜、奖励等，同时影响大量神经元的活动和可塑性(Marder, 2012)。
2.2. Related Work
许多先前发表的正则化方法(Kirkpatrick et al., 2017; Zenke et al., 2017; Kolouri et al., 2020; Chaudhry et al., 2018; Ahn et al., 2019)实现了类似于生物学中观察到的效果，修改损失函数以保留信息或规范模型的似然分布以保护重要的突触。EWC (Kirkpatrick et al., 2017)和SI (Zenke et al., 2017)等技术分别通过使用Fisher信息矩阵或跟踪突触在任务改进中的信度来选择重要参数。(Chaudhry et al., 2018; Kolouri et al., 2020; Lee et al., 2017)中提出的模型选择了保留任务潜在表征分布的参数。一个类似的研究方向是利用元可塑性进行持续学习。Laborieux et al. (2020)将一种元可塑性应用于二值神经网络模型，使权重更大的突触的可塑性更小，以保护它们免受后续训练的修改。
2.3. Main Contribution
通过结合突触巩固、元可塑性和神经调节，TACOS能够保护知识免受局部信息使用的灾难性干扰，无需求助于任务意识，并以有限资源运行，所有这些都是针对系统的重要特征实际部署。我们还展示了TACOS在受限于更现实的场景时的有效性，其中数据样本只看到一次。此外，我们探索了稳定性可塑性权衡，以确定网络在最优状态下执行的拐点以及该点对每个任务的数量和持续时间的依赖性。
3. Methodology
3.1. Problem Formulation
持续学习是序列学习任务的能力，在学习新任务时不会对先前学习的任务造成严重的性能损失。正式地，我们将任务Tt定义为一组的有序输入数据点对及其相应的类标签
。持续学习问题被表述为在序列训练时最大化系统在所有任务
中的性能。
3.2. Preliminaries
我们描述了在离散时间在SNN中进行持续学习的TACOS框架。基本构建块是脉冲神经元模型，即LIF神经元，其动力学描述为：
其中 t 是模拟时间步长计数器，Δt是时间步长的长度，膜电位V(t)随时间对突触电流I(t)进行积分，R是膜电阻，而τmem是膜时间常数，它控制积分和衰减的速率。突触电流是根据下式积分的突触前动作电位的总和：
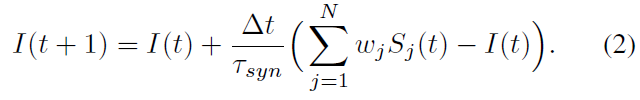
在每个时间步骤，突触输入电流I(t)由传入的N个突触前动作电位Sj的总和增加，Sj对已发放的神经元具有值1，否则为0，由突触强度wj加权，并随着突触时间常数τsyn呈指数衰减至零。
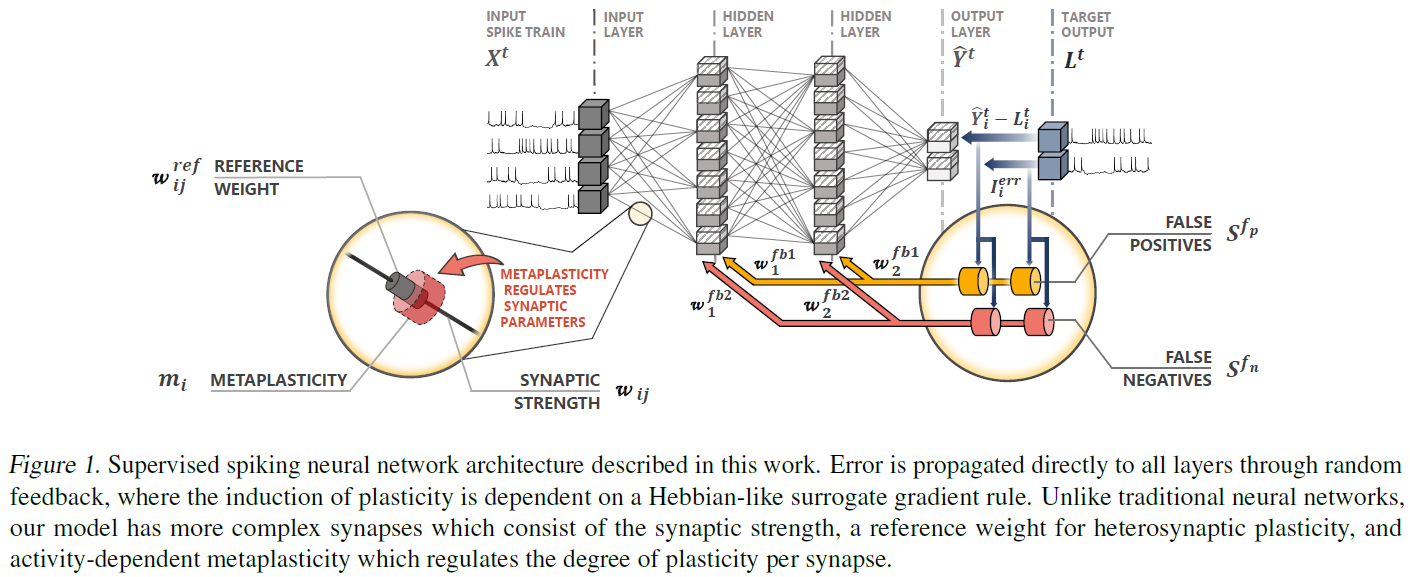
当膜电位超过阈值Vth时，发出动作电位(S = 1)，膜电位重置为零(V = 0)。任何最近被发放的神经元都会经历一段很短的时间，其膜电位被冻结在零，作为不应期的简单模型。这项工作中使用的神经网络是严格的前馈，如图1所示。输入作为脉冲序列接收，每个输入神经元一个，从输入数据生成，例如通过泊松或群体编码。
3.3. Surrogate Gradient Learning
为了训练模型，我们实现了一种替代梯度学习规则，称为事件驱动的随机反向传播(eRBP) (Neftci et al., 2017)。eRBP依赖于突触前发放、突触后替代梯度和通过固定随机权重的误差反馈，近似反向传播。在eRBP中，每个神经元都有第二个分量U (除了膜电位V)，用于整合误差反馈，如下所述。
（待续）
3.4. Continual Learning with eRBP
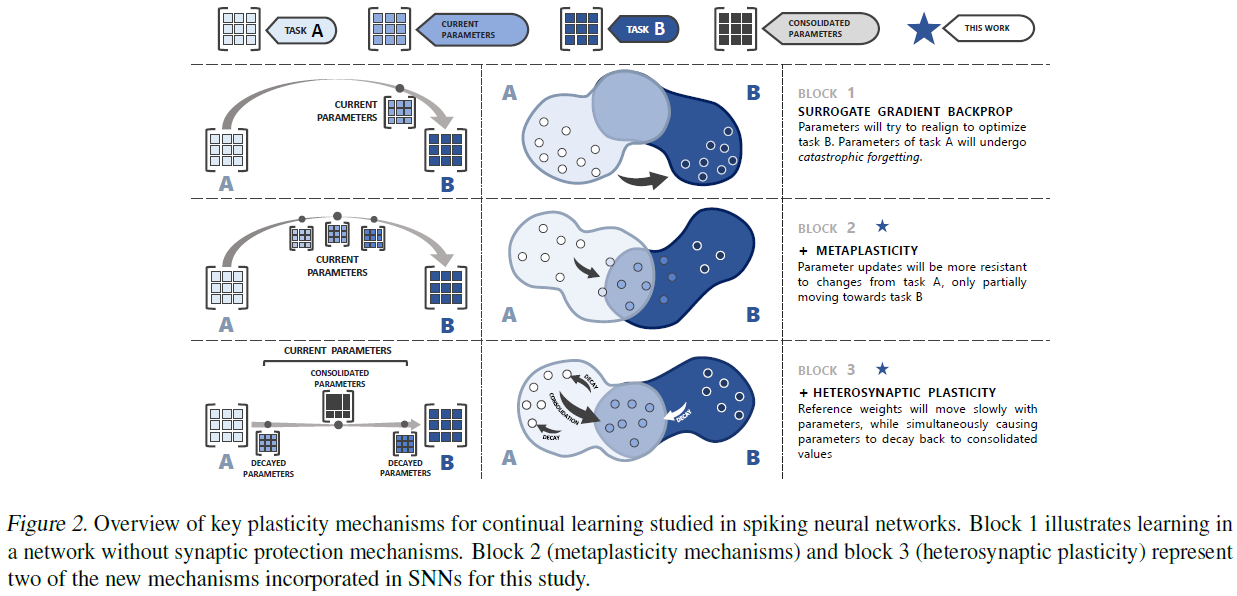
我们目前工作的目标是仅使用单个神经元和突触中局部可用的信息来保存突触知识。为了实现这一点，我们引入了神经启发的机制，以保留突触知识并增加突触本身的复杂性，如图2所示。
第一种机制，活动依赖的元可塑性，是对Laborieux et al. (2020)描述的技术的改编，其中突触的可塑性取决于它们当前的权重w和固定的元可塑性参数m。随着权重的增加，可塑性减弱，使得后续训练更难以修改突触。参数m的值控制了函数的严格程度：m值越大，可塑性衰减得越快。我们对这种机制的适应包括将m从全局参数更改为突触局部变量，该变量根据下式递增：
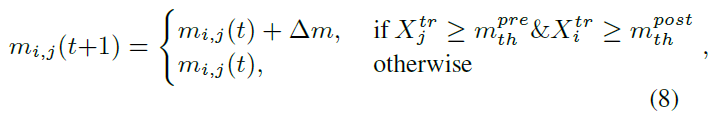
其中Δm是在由Xtr确定的合格突触处添加到m的固定增量，反映最近发放活动的神经元活动轨迹，以及突触前活动(
)和突触后活动(
)的阈值。使用动态可塑性水平来表示神经元对迄今为止所见的任务的贡献避免了将每个任务的最佳网络权重集存储为参考点的需要，同时使网络偏向于使用更多的可塑性神经元解决当前任务，这些神经元是在网络的生命周期中不太活跃的神经元。与使用基于幅度限制突触的固定元可塑性水平相反，动态元可塑性状态允许重要突触具有更大的稳定性，而无需在初始化时固有的高元可塑性状态，这会显著减慢学习速度。当将TACOS的应用扩展到涉及单次或少次学习的真实世界场景时，这一点尤其重要。然而，如果允许元可塑性无限增长，最终所有的突触都将变得无法训练。为了解决这个问题，我们强加了一个最大元可塑性状态，虽然它会导致一个饱和点，新任务的学习速度明显变慢，但仍然使突触能够持续学习。然而，为了真正规避这一限制，未来的工作可能需要允许元可塑性状态减少或利用神经发生。
突触的可塑性被计算为它的权重和可塑性参数的函数：
和用于调节权重更新，其中w是突触权重。
第二种机制称为突触巩固。一般的概念是，突触的复杂性比单个可塑性权重所能捕获的要复杂。一种方法是包括两个相互交互并且可能具有不同动态的权重分量，例如一种快速变化和一种缓慢变化(Zenke et al., 2015; Leimer et al., 2019; Munkhdalai, 2020)。在TACOS中，我们使用双分量模型，其中除了实际突触权重w之外，每个突触都有一个隐藏的缓慢变化的参考权重wref，它根据以下公式跟踪实际权重：
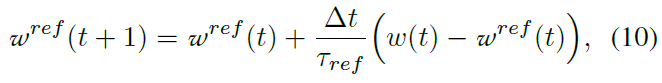
其中τref是wref(t)演化的时间常数。wref(t)的变化是由它与w(t)的差驱动的。
每当突触后神经元出现脉冲时，其所有传入突触的实际权重都会通过异突触可塑性向它们的参考权重漂移，根据：
其中α为衰减率。这种衰减回参考权重，取决于突触后活动，充当积极学习的神经元的正则化器。这有助于在当前突触变化和参考权重中存储的综合知识之间保持平衡。
总之，虽然元可塑性减缓了突触权重的变化，但它并不能阻止突触强度的长期变化。突触巩固与元可塑性协同工作以调节突触值的变化：i）参考权重的缓慢调整确保重复可塑性更新，由当前任务的误差调节可塑性驱动，将成为永久性的，ii）小的零星权重变化，通过元可塑性限制，在它们有时间巩固之前被异突触衰变消除，从而使突触权重保持在从先前任务中学到的值。TACOS中权重更新的完整公式为：
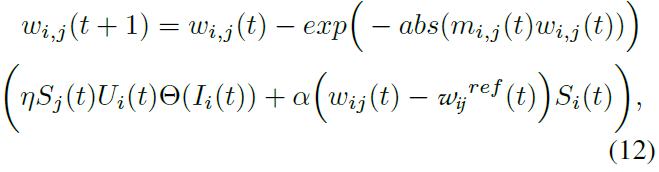
本质上，权重更新现在是来自误差驱动的替代梯度模型的更新和基于巩固机制的衰减项的组合。元可塑性用于控制由误差驱动的可塑性和衰减引起的变化强度。这些机制结合在一起以减轻灾难性干扰，仅依赖于局部信息。
4. Results
我们使用5-Split MNIST (LeCun et al., 1998)和Fashion-MNIST (Xiao et al., 2017)数据集在任务不可知域增量持续学习场景(van de Ven & Tolias, 2019; Hsu et al., 2018)，其中任务共享相同的输出层，而模型在训练和推理期间都不知道任务身份。网络配置固定为每个隐藏层200个神经元(1-2个隐藏层)，以及两个神经元的输出层。与大多数模型不同，TACOS只看到每个数据样本一次(即一个训练时期)，就像现实世界中的情况一样(Lopez-Paz et al., 2017)。
Continual Learning Analysis:
TACOS Plasticity-Stability trade-off:
5. Conclusion
TACOS结果表明，使用局部可塑性机制的组合可以在脉冲网络中实现持续学习。具体来说，我们证明了活动依赖的元可塑性、突触巩固、异突触衰减和误差驱动的神经调节的组合可以在域-IL场景中胜过类似的基于发放率的模型。至关重要的是，TACOS以与任务无关的方式实现了这一点，仅依赖局部信息，内存预算不会随着任务数量的增加而增加。通过探索稳定性-可塑性权衡作为元可塑性的函数，我们证明了活动依赖的元可塑性比固定的元可塑性状态提供了显著的改进。随着SNN中学习模型的进步，TACOS中展示的机制将适用于CNN以解决更复杂的问题，例如Cifar10/100和ImageNet。在未来的工作中，我们预计通过以下方式进一步促进TACOS：i）允许减少元可塑性状态，ii）结合神经发生以引入具有低元可塑性状态的神经元，或 iii）当知识的长期巩固可以通过排练发生时重置元可塑性状态。