郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

arXiv:2008.13044v1 [cs.LG] 29 Aug 2020
Abstract
脉冲神经元网络已成功用于解决简单的强化学习任务,其中连续动作集应用基于脉冲时序依赖可塑性(STDP)的学习规则。然而,这些模型中的大多数不能应用于具有离散动作集的强化学习任务,因为它们假设所选动作是神经元发放率的确定性函数(它是连续的)。在本文中,我们提出了一种新的基于STDP的学习规则,用于包含反馈调节的脉冲神经元网络。我们表明,当应用于CartPole和LunarLander任务时,基于STDP的学习规则可用于以类似于标准强化学习算法的速度解决具有离散动作集的强化学习任务。此外,我们证明如果从学习规则中省略反馈调节,智能体将无法解决这些任务。我们得出结论,当只有对执行的动作和TD误差有贡献的单元参与学习时,反馈调节允许更好的信度分配。
1 Introduction
近年来,脉冲神经网络(SNN)在解决机器学习任务方面越来越受欢迎[1-4]。尽管如此,深度学习的最新进展主要集中在人工神经网络(ANN)而不是SNN,部分原因是可以通过反向传播有效地训练ANN,而SNN存在反向传播问题,因为它们的单元通过二值脉冲进行通信,因此网络是不可微的[5]。然而,通常认为反向传播在生物学上是不可信的[6]。然而,已经在生物神经系统中通过实验观察到脉冲时序依赖性可塑性(STDP)和奖励调节STDP (R-STDP)[7]。STDP可以通过最大化突触前神经元和突触后神经元之间的互信息在理论上推导出[8],而R-STDP可以通过最大化全局奖励信号在理论上推导出[9, 10]。
以前的工作在使用基于STDP的学习规则使用SNN解决强化学习任务方面取得了一些成功。对于具有连续动作集的任务,[11, 10]表明R-STDP或TD-error-modulated STDP (TD-STDP),一种类似于R-STDP的学习规则,但用时序差分误差(TD error)代替奖励,可用于解决具有连续动作集的强化学习任务,例如迷宫任务和倒置的CartPole。[12]展示了使用R-STDP解决车道保持任务的成功。
对于具有离散动作集的任务,[13]使用了群体SNN来成功学习诸如Mountain Car和CartPole之类的任务,但学习速度比标准强化学习算法慢得多。[14]成功地解决了网格世界的任务,但他们的算法只能应用于具有有限和中等数量状态的任务。[15]使用R-STDP来解决Pong的简化版本。
在这些SNN模型中([13]除外),选择的动作是actor神经元发放率的确定性函数,因此它们只能依靠脉冲序列的随机活动来鼓励探索。然而,这种鼓励探索的方式效率低下,因为所有神经元都很难对齐它们的独立随机噪声。例如,当使用一组神经元发放率的平均值作为动作强度时,探索所需的随机噪声在取平均值后大部分会被抵消。这种探索方法只有在动作集是连续的并且奖励函数是动作的连续函数时才有效,因为动作中非常小的随机噪声就足以估计回报的变化,这本质上等同于通过数值近似的梯度估计。如果动作集是离散的,并且使用阈值函数将发放率转换为动作,则梯度几乎处处为零,如果噪声太小,则不会进行探索。
Actor-Critic算法是强化学习中最早和最流行的方法之一[16, 17]。Actor-Critic算法的actor学习规则类似于R-STDP的长期增强(LTP)端,但状态被SNN中传入脉冲的迹所取代。还假设actor和critic网络可能对应于生物神经系统中纹状体的背侧和腹侧细分[18],而TD误差代表生物神经系统中的多巴胺调节[19]。
最近的神经科学研究表明,反馈联系可能在学习和注意力中发挥作用。[20]总结了表明学习突触权重存在反馈调节的不同证据,并陈述了一个门控假设来解释这些证据,这表明"响应选择引发反馈信号,使上游突触具有可塑性"。我们提出的反馈调节的TD-STDP学习规则对应于这个假设。[21, 22]还提出了基于发放率神经元的反馈调节学习规则。由于本文的主要目标是用SNN解决强化学习任务,我们建议读者参考[20]中有关神经科学中反馈调节的相关工作。
在本文中,我们研究了如何使用基于SNN和STDP的学习规则通过离散动作集有效地解决强化学习任务。我们提出了一个actor-critic架构,将actor神经元的输出视为选择动作的概率而不是动作本身。由于选择的动作不再是actor神经元输出的确定性函数,我们还提出了一种新的学习规则,我们称之为反馈调节TD-STDP,以实现更好的信度分配。我们表明,新的反馈调节TD-STDP学习规则可用于以类似于标准强化学习算法的速度解决常见的强化学习任务,例如CartPole和LunarLander。同时,TD-STDP和R-STDP在没有反馈调节的情况下无法学习任务。
需要指出的是,最近一项独立于我们开发的工作提出了一个类似于我们的学习规则,称为e-prop[23]。它基于时间反向传播(BPTT),论文表明它可以有效地解决一些Atari游戏。他们提出的用LIF神经元解决强化学习任务的学习规则与我们的方法有几个不同:(i) 我们在STDP中使用LTD,而他们不使用这样;(ii) 他们在计算突触前迹时使用不同的方法;(iii) 我们使用更复杂任务所需的正则化。我们的论文在[23]发表之前提交给同行评审会议,我们在提交论文之前并不知道这项研究。除了[23],我们不知道有任何先前的工作使用SNN和基于STDP的学习规则来解决具有离散动作集的常见强化学习任务,其速度类似于标准强化学习算法。
本文介绍的结果为SNN与强化学习相结合以有效解决机器学习问题的更广泛应用开辟了前景。
2 Background
2.1 Markov Decision Process
2.2 Spiking Neural Network (SNN)
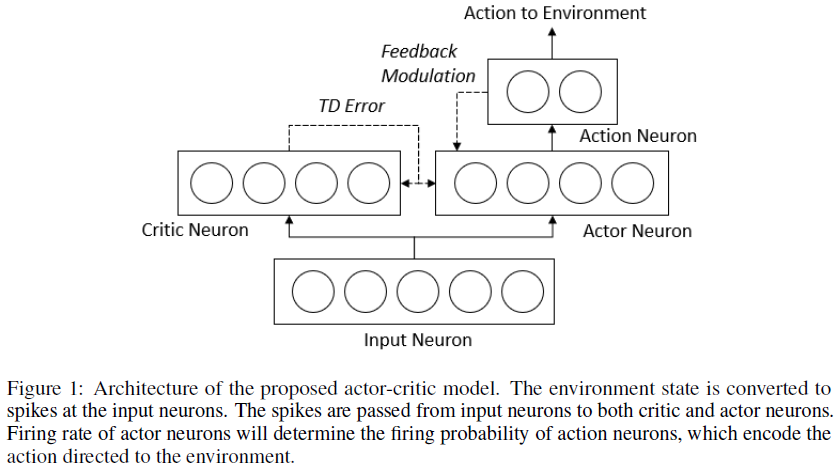
3 Model
所提出的模型架构如图1所示,它基于actor-critic架构。我们将在以下部分讨论每组神经元。
3.1 Critic Neuron
3.2 Learning Rule for Critic Neuron
3.3 Actor and Action Neuron
3.4 Learning Rule for Actor Neuron
3.5 Regularization in SNN
3.5.1 Entropy Regularization
![]()

![]()
3.5.2 Weight Decay
权重衰减或L2权重正则化也有利于训练SNN。由于我们在模型中没有对权重范数施加任何限制,因此我们观察到一些actor神经元几乎在每一步都在发放。但是actor神经元的绝对发放率水平并不重要。只有actor神经元发放率的相对水平决定了选择一个动作的概率。通过每一步发放,上述学习规则不再能进一步提高神经元的发放率。因此,需要某种形式的正则化来保持actor神经元的绝对发放率水平较低,以便上述学习规则在控制发放率方面有效。我们发现使用权重衰减可以实现这样的正则化。将cw表示为权重衰减的强度,将(14)中的学习规则修改为:
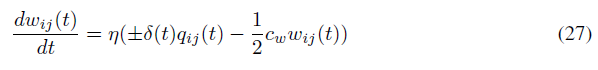
3.5.3 Target Firing Rate


4 Experimental Results
4.1 CartPole
4.2 LunarLander
5 Conclusions
本文的目标是使用SNN有效地解决具有离散动作集的强化学习任务。在我们的方法中,Actor-Critic架构将actor神经元的输出视为选择动作的概率,而不是动作本身。我们为具有Actor-Critic架构的SNN推导出一种新的学习规则。由于选择的动作不再是actor神经元输出的确定性函数,我们提出了一种新的学习规则,我们称之为反馈调节TD-STDP,以实现更好的信度分配。
我们表明,我们的学习方法可用于以与标准强化学习算法相当的速度解决CartPole和LunarLander。使用具有生物学启发的学习规则的SNN来有效解决强化学习任务的可能性可以提供有关学习如何在生物神经系统中发生的提示。例如,我们表明我们提出的学习规则中的反馈调节对于智能体学习是必要的,这可能表明反馈连接在生物神经系统中的可能作用之一是结构信度分配。
最近开发了一种类似于我们的学习规则,称为e-prop[23]。它基于时间反向传播(BPTT),并且表明学习规则可以有效地解决一些Atari游戏。E-prop和我们的方法有几个不同之处:(i) 我们在我们的学习规则中包含了STDP的LTD方面;(ii) 在计算突触前迹时,他们使用![]() ,而我们使用
,而我们使用![]() ;(iii) 我们提出了解决更复杂任务所必需的正则化方法。
;(iii) 我们提出了解决更复杂任务所必需的正则化方法。
除了更复杂的方法来鼓励探索之外,未来可能的工作还包括通过模型学习隐藏表征,这可以应用于基于像素的游戏,例如Atari。[32, 33]表明STDP可用于训练SNN以提取有用的特征以进行图像分类。这些方法可用于在我们提出的模型中为actor和critic网络训练隐含层,并指出学习多层SNN以解决复杂的强化学习任务而无需反向传播的可能性。
SNN和ANN在学习强化学习任务中的比较也值得进一步研究。由于生物神经系统中的神经元通过脉冲进行通信,因此SNN通常被认为比ANN更接近生物神经系统。除了低通信成本之外,SNN在学习方面比ANN有什么优势吗?SNN是否允许更快的学习或更强大的策略学习?我们希望这项工作可以鼓励更多人关注SNN,并可以进一步推动使用SNN解决更复杂的强化学习任务。
A Theoretical Derivation of TD-STDP and Feedback-modulated TD-STDP
A.1 Proof of Theorem 1
A.2 Proof of Theorem 2
B Formulas in Discrete Time Step