郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

PloS one, no. 3 (2015): e0115620-e0115620
Abstract
RL的理论框架在理解动物的动作选择中起着重要作用。SNN提供了一种基于理论的手段,可以通过数值仿真对RL的神经学合理算法进行计算假设测试。但是,尽管这些模型是不可避免的,并且限制了实际环境中的学习功能,但是大多数模型无法处理嘈杂的或过去发生的观察。此类问题在形式上被称为部分可观察的RL (PORL)问题。它提供了对部分可观察领域的RL的泛化。另外,现实世界中的观察往往是丰富且高维的。在这项工作中,我们使用SNN模型来近似受限玻尔兹曼机的自由能,并将其应用于具有高维观测的PORL问题的求解。我们的脉冲网络模型通过感觉上模棱两可的高维观测来解决迷宫任务,而无需了解真实的环境。具有工作记忆的扩展模型还可以解决与历史相关的任务。SNN处理PORL问题的方式可能使你了解神经信息处理的基本规律,而只有通过这种自上而下的方法才能发现这些规律。
Introduction
当面对一个新颖的环境时,动物会通过试错来学习采取什么动作。这种不完全了解环境的奖励驱动学习称为RL [1]。从表明奖励预测误差与多巴胺信号相关的突出实验结果开始[2],许多研究已经研究了如何在大脑中实现RL算法[3-5]。
SNN的数值仿真可用于测试奖励学习算法在神经上是否合理,并在理论上研究计算假设的有效性。在SNN中,有几种成功实现RL的方法[6-11]。
但是,在许多现实情况下,动物所面临的问题比用RL可以解决的问题更具挑战性。观察通常是嘈杂且随机的,而最优的决策通常取决于过去的经验。RL泛化到这种部分可观察的域被称为部分可观察的RL (PORL)[12]。根据任务难度,可以将PORL问题分为两个子类。当最优策略取决于当前观察时,我们称这种情况为历史独立的PORL问题。另一方面,当最优策略取决于过去的观察时,我们称这种情况为历史依赖的PORL问题。PORL问题提供了一个框架,可以在不完全了解环境的情况下解决部分可观察的马尔可夫决策过程(POMDP)。它在理论上牢固扎实,并且也足以在现实世界中对动物的决策建模。已经提出了几种算法来解决PORL问题[13-16]。这些算法从过去的观察,执行的动作和获得的奖励的序列内部构造一个近似的马尔可夫状态。
其中,有一种算法可以使用基于随机系统自由能的方法(例如,受限玻尔兹曼机:RBM)解决PORL问题[15]。这是Sallans and Hinton方法[17]的扩展,该方法能够处理高维二值状态和动作。我们称这些方法为基于自由能的强化学习(FERL)框架。使用FERL,已知感觉信息以目标导向的方式编码在神经群体的激活模式中。这种方法在SNN中的实现应提供自上而下的一瞥,以了解基于奖励的学习的神经算法。在这项工作中,我们提出了FERL的SNN实现,并将其应用于几种类型的PORL任务的解决方案。
该论文的组织方式如下:首先,在Material and Methods部分中,我们介绍了FERL以及如何扩展它来解决PORL问题。我们还介绍了在SNN中实现其所需的概念,例如伪自由能。然后,在Results部分中,我们在难度增加的三个任务上测试我们的SNN模型:中心到达任务(RL问题),数字中心到达任务(独立于历史的PORL问题)和数字匹配T迷宫任务(历史相关的PORL问题)。最后,在Discussion部分中,我们解释我们的结果以阐明该方法的其余问题,并从生物学的角度对我们的结果进行解释。
Methods
Free-energy-based reinforcement learning
Sallans and Hinton[17]将受限玻尔兹曼机(RBM)框架的应用从无监督学习和监督学习扩展到RL。我们称其为在RL中使用基于能量的建模的方法基于自由能的RL (FERL)。这是因为它使用随机系统的自由能来捕获在RL中出现的重要量。RBM是基于能量的统计模型(也称为"无向图模型"或"Markov随机域"),其中二值节点被分为可见层和隐含层。可见层中的节点全连接到隐含层中的节点,但是同一层中的节点之间没有连接。由于这种受限的连通性,给定可见节点的值,隐含节点上的后验分布变得有条件独立,并且无需大量计算就可以精确地进行计算。在FERL中,可见层中的二值节点进一步分类为状态节点s和动作节点a。
RBM的能量函数为:
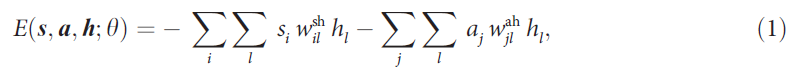
(省略)
Implementation with spiking neuron
Leaky integrate-and-fire neuron
Network architecture
Approximation of free-energy
Working memory
Observation
Simulation settings
Results
Center reaching task
Digit center reaching task
Digit matching T-maze task
Discussion
Comparison with the original RBM
Learning ability with aFE and iFE
Working memory architecture
Biological plausibility
Supporting Information
S1 Fig. Characteristics of the pretrained weights between the observation layer and the memory layer.
S2 Fig. Estimation of iFE by sequential manner.