A Spiking Neural Network Model of an Actor-Critic Learning Agent

摘要：郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Neural Computation, no. 2 (2009): 301-339

Abstract

　　与环境交互而适应行为以最大化奖励的能力对于任何高级生物的生存至关重要。在RL框架中，TD学习算法为这种目标导向的适应提供了有效的策略，但尚不清楚这些算法在多大程度上与神经计算兼容。在本文中，我们提出了一个SNN模型，该模型通过将局部可塑性规则与全局奖励信号相结合来实现actor-critic的TD学习。该网络能够以稀疏奖励解决非平凡的gridworld任务。我们得出可塑性参数和突触权重到标准算法公式中相应变量的定量映射，并证明网络以与其等效离散时间算法相似的速度学习，并获得相同的均衡性能。

1 Introduction

　　神经科学中的一个普遍问题是如何在细胞水平上实现系统级学习。这是一个基本的假设，突触可塑性是学习的基础，但是在高等生物中，突触功效的描述水平与动物行为的描述水平之间的差距仍未消除(但请参阅Antonov, Antonova, Kandel, & Hawkins, 2003)。一种学习模型吸引了可观的关注，那就是强化学习(RL)。与监督学习需要明确的教师信号不同，RL仅需要评估反馈，该反馈可能是带噪的或稀疏的。RL智能体试图最大化从环境中获得的奖励。这更符合自然界中动物所遇到的大多数学习情况，在自然世界中，动物缺乏直接的监督，但是饥饿，饱腹，痛苦和愉悦之类的奖励和惩罚比比皆是。行为和神经生理学研究有大量证据表明，动物会进行某种RL。尤其是，许多结果可以由称为TD学习的RL变体来解释，其中连续时间的奖励估计被比较。通过比较奖励估计而不是等待来自环境的奖励，TD学习系统可以有效地解决奖励稀疏的任务。TD学习已被用来解释多巴胺神经元在非人类灵长类动物的奖励学习中的活动(Schultz, Dayan, & Montagu, 1997; Schultz, 2002)。在人类中，多巴胺依赖的预测误差已被证明可以指导决策(Pessiglione, Seymour, Flandin, Dolan, & Frith, 2006)。此外，在人类功能性神经影像学中，发现血氧水平依赖(BOLD)活动与TD学习算法所需的误差信号之间存在高度相关性(O'Doherty, Dayan, Friston, Critchley, ＆ Dolan, 2003; Seymour et al., 2004)。它也已用于在不确定环境中对蜜蜂觅食进行建模(Montague, Dayan, Person, & Sejnowski, 1995; Niv, Joel, Meilijson, & Ruppin, 2002)和人类决策(Montague, Dayan, ＆Sejnowski, 1996)。在机器学习领域，TD学习已成功应用于各种应用中，例如双陆棋(Tesauro, 1994)，Cartpole (Barto, Sutton, ＆ Anderson, 1983)和机器人控制(Mor​​imoto ＆ Doya, 2001)。有关TD学习和通用强化学习的全面介绍，请参见Sutton and Barto, 1998; Bertsekas and Tsitsiklis, 1996。

　　但是，尚不清楚如何在大脑中实现TD学习。TD学习的经典公式是分步定义的。在每个步骤中，智能体都会选择一个动作，并传达给环境。环境以信号通知智能体其新状态。因此，将一个状态的奖励估计与上一步所占状态的奖励估计进行比较是一种简单的操作。神经元在连续时间内通过脉冲进行交互，因此尚不清楚如何定义"上一步"的概念，或者应该比较哪个可观察量。由于这种不兼容性，以前的建模尝试通常集中在非TD强化学习策略(Seung, 2003; Xie ＆ Seung, 2004; Florian, 2007; Baras＆Meir, 2007)或非脉冲模型(Suri and Schultz, 1999, 2001; Foster, Morris, ＆ Dayan, 2000)。前一类证明了SNN可以解决诸如XOR问题之类的简单任务，在XOR问题中，每做出一次网络决策都会奖励或惩罚。尚未显示出这种网络以稀疏奖励解决更困难的任务的能力。在后一类中，Foster et al. (2000)已经表明，不学习TD学习的神经元实现能够解决复杂的任务，但是尚未有一个先验清楚如何通过连续时间内运行的突触来实现模型中离散的突触权重更新。第三类研究是在突增活动的背景下研究TD学习的各个方面。然而，他们只关注预期何时可以获得奖励的预测问题，而没有解决采取何种动作的控制问题(Rao ＆ Sejnowski, 2001)，或者仅关注简单的控制问题，即在每个决定后都会给予奖励或惩罚(Izhikevich, 2007; Farries ＆ Fairhall, 2007)。

　　我们首次提出了一个SNN模型，该模型通过实现完整的actor-critic TD学习智能体同时解决了预测和控制问题(请参阅第2节)。学习过程背后的突触可塑性依赖于突触前和突触后活动以及整体奖励信号的生物学合理的度量。我们进一步显示了突触动态和TD算法的离散时间公式之间的等效关系(在1.1节中进行了综述)，从而得出了离散时间公式的参数与神经元公式的参数之间的定量映射(请参见第3节)。神经网络可以解决稀疏奖励的非平凡gridworld任务，其速度几乎与等效离散时间算法的实现速度相同，并且具有相同的均衡性能(请参阅第4.1节)。我们表明，导出的映射具有很高的精度(请参见第4.2节)。对于广泛的参数，性能和映射仍然很鲁棒。如果智能体仅在很短的时间内占据每个状态，则映射精度会降低，但是网络的学习行为会保持鲁棒，直到达到限制的时间跨度(请参阅第4.3节)。此处研究的突触更新规则仅代表TD学习的一种可能实现。我们将在第5节中讨论替代实现。

　　初步工作已经以抽象形式提出(Potjans, Morrison, ＆ Diesmann, 2007a, 2007b)。

1.1 Actor-Critic Temporal-Difference Learning

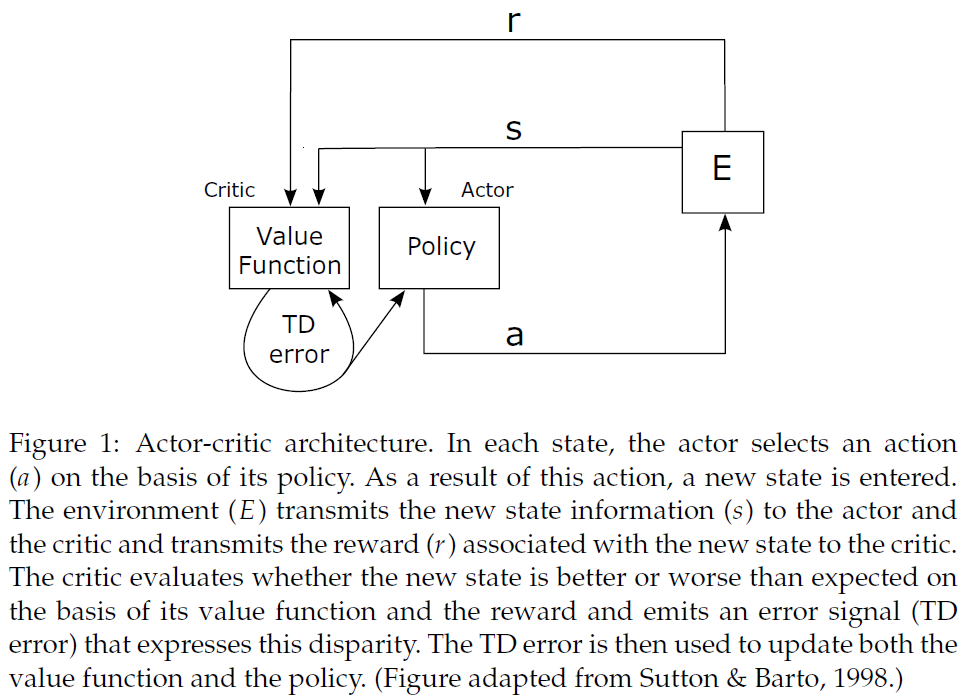
　　RL智能体的目标是最大化随着时间的推移而从环境中获得的奖励。当智能体收到奖励(或惩罚)时，一个主要问题是如何在导致奖励(或惩罚)的决策之间分配强化；这被称为时序信度分配问题。TD学习是解决这一问题的一种特别有效的方法。在此，我们关注TD学习的一种变体，即actor-critic架构(Witten, 1977; Barto et al., 1983)。关于TD学习和这里提出的actor-critic算法的全面介绍可以在Sutton and Barto, 1998中找到。actor-critic结构的两个模块(参见图1)之所以被调用，是因为actor选择在给定的状态下执行哪个动作，并且critic评估所选动作的结果。在每个离散时间步骤中，环境将其状态传输给智能体。actor通过使用策略π(s, a)来选择一个动作，该策略给出了在状态s中选择动作a的概率。作为该动作的结果，在下一个时间步骤中，环境将把一个新状态以及与新状态相关联的任何奖励传递给智能体。另外，在每一个时间步骤中，通过利用一个价值函数V^π(s)，critic评估当前状态在多大程度上比以前的状态有所改进。价值函数可以理解为在时间步骤 i 从给定状态s开始并遵循策略π时获得的期望折扣未来奖励总和：

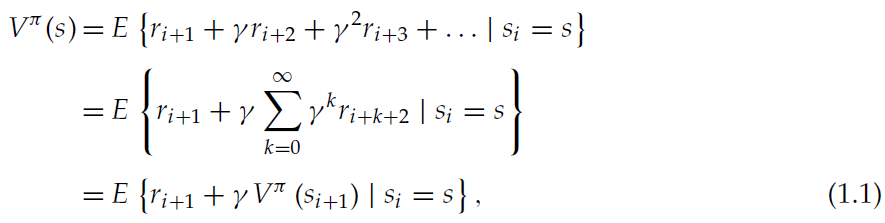
其中E{·}表示期望价值，r_i+k是在k个时间步骤之后访问的状态所给予的奖励，而γ是介于0和1之间的折扣因子。在学习过程中，只有实际价值函数V^π(s)的估计V(s)。价值函数的连续估计通常不满足公式1.1中给出的自一致性关系。这种差异称为TD误差：

δ_i的符号和大小包含关于V^π(s)的估计如何根据自一致性进行调整的信息。如果TD误差为正，这意味着新状态s_i+1比期望的要好，因此V(s_i)需要增加。反之，如果TD误差为负，则新状态比期望的差，因此V(s_i)应减小。δ_i的大小表明V^π(s)的当前估计值偏离多远。这将导致V(s_i)的更新规则：

其中α是一个小的正步长参数。这被称为TD(0)算法(Sutton, 1988)，对于足够小的α，它对于概率为1的给定策略收敛(Dayan, 1992; Dayan & Sejnowski, 1994)。这解决了确定特定策略π的价值函数V^π的预测问题。为了解决控制问题(即确定任务的最优策略)，actor还利用TD误差信号中编码的信息来相应地调整策略。正TD误差表示所选动作a导致的状态比期望的要好；因此，下次智能体处于状态s时选择此动作的概率应增加。同样地，负TD误差意味着下次智能体处于s状态时选择此动作的概率应该降低。例如，如果选择动作的概率由Gibbs softmax方法给出，

其中p(s, a)是对状态s中动作a偏好的度量，那么π可以通过更新向最优策略更新

其中β是另一个小步长参数。这样，最优策略和相关价值函数可以逐步地学习，纯粹是通过智能体自己对环境的探索。

　　实现价值函数的最简单方法是使用一个查找表，每个状态有一个条目。这种结构所需的内存随状态数线性增加。类似地，在离散动作的情况下，策略可以用一个查找表来表示，在该表中，每个状态对于每个动作都有一个条目。因此这种结构所需的内存量随状态数和可能动作数的乘积线性增加。而且，由于每个状态都需要多次访问才能获得价值函数的良好近似，增加状态数通常会导致学习速度变慢。因此，上面提出的算法非常适合于状态和动作数量较少/中等的任务。为了解决具有大量状态和动作的问题，需要某种泛化。一种方法是将actor-critic算法解释为一种随机梯度算法，其中critic使用一种确定参数化策略更新的近似架构来实现TD学习(Konda & Tsitsiklis, 2003)，其中已经确定了收敛准则。由于我们在这篇文章中的目的是证明SNN实现TD学习的原理，下面我们将自己局限于上面概述的简单表格式算法。

2 Spiking Neuronal Network Model

　　网络的结构(编码价值函数和策略的神经元模块和突触)在2.1节中介绍。为了清楚起见，分别介绍了将价值函数和策略收敛到最优价值的突触动态(第2.2节)。所有仿真的详细信息在附录A中给出。

2.1 Network Architecture

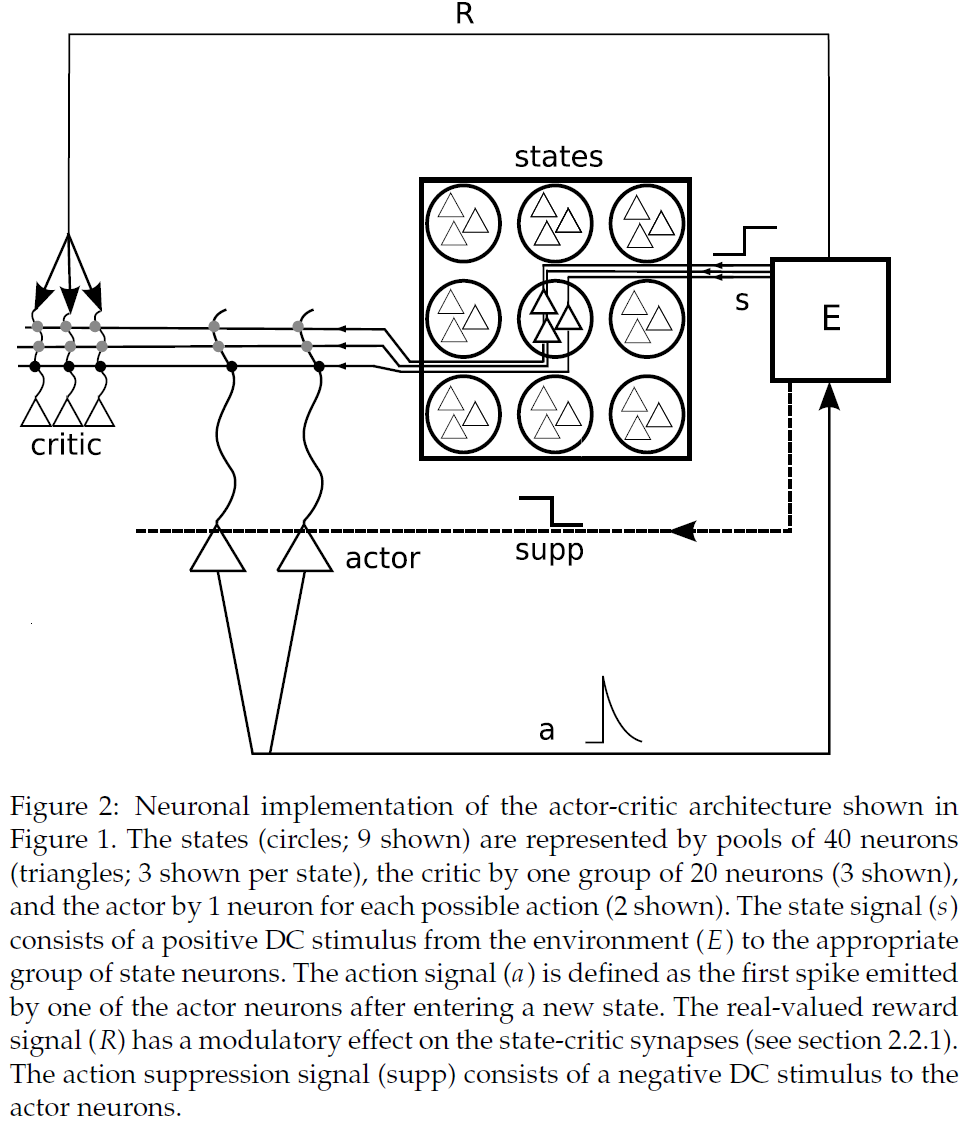
　　图2中所示的网络结构受actor-critic架构的启发，与Foster et al. (2000)研究的非脉冲网络相似。该智能体由三个基于电流的LIF神经元模块组成：actor模块、critic模块和状态模块。智能体与环境交互，在本文中，环境是纯算法实现的。环境通过向相应的神经元提供DC刺激来激活一个状态的表征，使它们以42.63 Hz的频率发放；在失活状态下，它们的发放率为0.01 Hz。环境同时在短时间内抑制动作模块(动作抑制期)，以使状态神经元的活动增强。状态神经元投射到actor模块和criter模块。激活状态和一个给定的actor神经元之间的突触权重越大，它首先被激活的可能性就越大。无论哪一个actor神经元对一个状态的激活做出第一反应，都会被环境解释为所选择的动作(关于初次脉冲编码的回顾，见VanRullen, Guyonneau, Thorpe, 2005)。因此，状态神经元和actor神经元之间的突触权重编码智能体的策略。作为所选动作的结果，环境将取消激活先前的状态并激活由环境模型确定的新状态。如果新状态与奖励相关联，环境会发出一个恒定的奖励信号R，直到智能体再次离开状态。状态神经元和critic神经元之间的突触权重编码智能体的价值函数。因此，如果智能体从与低价值相关的状态移动到与高价值相关的状态，则critic神经元的发放率增加。相反，从高价值状态移到低价值状态会导致critic发放率降低。

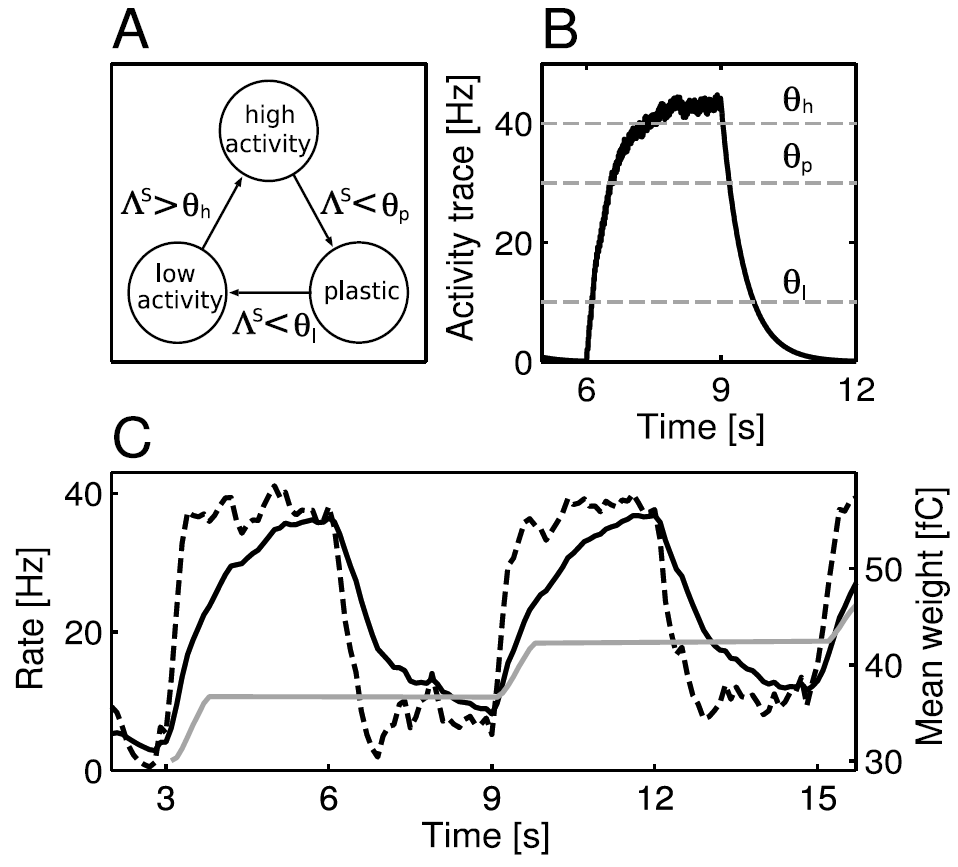
图3：状态-critic突触的可塑性。(A) 突触可以采用三种状态：低活性，高活性和可塑的。转换受突触前活动迹Λ^s上的阈值(θ_h, θ_p和θ_l)控制。(B) 突触前活动迹Λ^s与时间的关系。在6 s时，刺激突触前神经元产生42.6 Hz的发放率；在9 s时，刺激被关闭。灰色虚线表示θ_h, θ_p和θ_l的值，这些值触发了A中描述的转换条件。(C) 突触后活动迹以及由此产生的状态-critic权重发展与时间的关系。所讨论的状态由40个突触前神经元表示，这些神经元投影到20个神经元的critic模块中(见图2)。该智能体从突触前神经元代表的状态移出，在3s, 9s和15s进入较高价值的状态。当智能体离开状态时，突触变成可塑的(参见B)，而权重的变化取决于两个突触后活动迹之差。快速的突触后活动迹(黑色虚曲线，在所有突触后神经元上取均值)比落后的突触后活动迹(黑色实曲线，在所有突触后神经元上的均值)更快地适应发放率的变化。因此，每当智能体离开状态时，状态-critic突触的权重(灰色曲线，在800个突触上取均值)会增加，否则保持不变。

2.2 Plasticity

2.2.1 State-Critic Plasticity

　　在本节中，我们为状态神经元和critic神经元之间的突触权重制定更新规则，该规则编码神经元智能体的价值函数，即TD(0)算法的价值函数更新的生物学合理实现，公式1.3。要获得这样的规则，必须考虑价值函数更新的三个重要属性。首先，并非所有价值都同时更新。当智能体从状态s_i转到状态s_i+1时，仅更新V(s_i)。其次，更新分别取决于当前状态和后续状态的价值V(s_i)和V(s_i+1)。第三，更新取决于与状态s_i+1相关的外部奖励r。在神经元框架中，我们可以将这些属性解释如下：

1. 状态-critic突触的可塑性可以忽略不计，除非在智能体刚离开相应状态的短时期内。可塑性间隔小于智能体通常保持一种状态的时期。
2. 状态-critic突触对critic神经元的特征性动态反应敏感，后者编码刺激的变化。
3. 状态-critic突触对代表奖励的全局信号敏感。

另外，突触更新规则应该是生物学合理的，因为它是连续制定的，不需要时钟信号，并且很大程度上依赖于局部信息。在下文中，我们提出并测试候选突触更新规则；但是，约束条件并不需要唯一的规范，因此此处介绍的规则应仅作为一类适当规则的示例。更多示例在第5节中讨论。

　　为了使突触能够检测到智能体何时离开与突触关联的状态，必须标识编码此信息的局部可用信号。一个这样的信号是突触前发放率：当智能体离开状态时，该信号从高值下降到低值，因为环境不再刺激与该状态相关的状态神经元(请参阅第2.1节)。尽管从突触的观点来看，突触前神经元的发放率不是直接可测量的量，但是突触前神经元的单个脉冲被认为是可直接测量的。因此，我们可以通过活动迹近似脉冲时间特定实现的发放率，定义为：

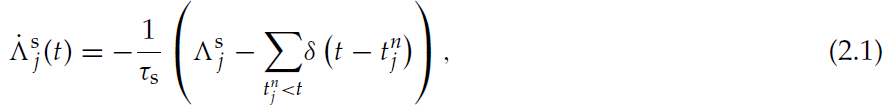
其中是突触前神经元 j 的第n个发放时间，而τ_s是活动迹的时间常数。这是突触前脉冲序列的低通滤波版本。有关由此类变量实现的可塑性规则的综述，请参见Morrison, Diesmann, and Gerstner, 2008。我们提出，突触可以处于三种活动依赖状态：高活性，低活性和可塑的(见图3A)。当它的活动迹超过相应阈值时，就会发生从一种活动依赖状态到另一种状态的转换。图3B中显示了状态-critic突触的活动迹的实现(带有三个阈值)。在下面，让我们假设状态神经元 j 是代表状态x的神经元组的一部分。在智能体到达x之前，突触前发放率较低，因此突触处于低活性状态。当智能体到达x时，代表该状态的所有神经元都会受到刺激，导致发放率的增加，从而导致神经元 j 的所有状态-critic突触的活动迹的增加。当超过阈值θ_h时，突触进入高活性状态。当智能体离开x并到达不同状态时，代表x的神经元不再受到刺激，因此它们的发放率降低。指数减小到阈值θ_p以下，并且突触到达可塑状态。当活动进一步降低到阈值θ_l以下时，突触重新到达低活性状态。在低/高活性状态下，突触是静态的；到达和离开可塑状态的转换定义了由智能体离开x触发的可塑性间隔，从而满足了上面讨论的价值函数更新的第一个属性。请注意，当智能体离开x时，只有与x相关的状态-critic突触才是可塑的，所有其他状态-critic突触将处于低/高活性状态。如果选择的动作没有导致新状态，则与x关联的状态-critic突触将保持在高活性状态，并且不会进行学习。这与传统的离散时间TD(0)算法有所不同，传统的离散时间TD(0)算法在每个时间步骤更新价值函数，而与选择的动作是否导致新状态无关。但是，对于状态数量适中且奖励稀疏的任务，这种偏差不太可能导致性能变差。对于奖励稀疏的问题，折扣因子γ的一个好的选择接近于1，因为它可以使智能体具有远见。根据公式1.1和1.2，价值函数更新(当被选择的动作不导致新状态时)与(γ-1)V(s_i)成比例，即它小到可以忽略。我们显示在4.1节中的是这种偏差不会导致我们的测试任务性能变差。

　　TD(0)学习中价值函数更新的第二个属性要求比较两个连续状态的价值。为了在神经元连续时间公式中实现此属性，突触需要信息，该信息编码在其可塑性间隔期间先前状态和当前状态的价值。由于状态价值用相应状态-critic突触的强度进行编码，因此表达状态价值的合适局部可用信号就是critic神经元的发放率：突触强度越大，critic神经元发放率就越高。假设由于反向传播或其他机制，突触后脉冲可以由突触直接测量，则突触后发放率可通过脉冲序列的低通滤波器进行近似计算，如公式2.1所示。

　　为了同时为突触提供有关两个连续状态的信息，我们假设突触后神经元k的脉冲在突触处贡献了两个突触后活动迹：快速迹和落后(或慢速)迹，其中时间常数τ_r < τ_l。由于落后活动迹所包含的有关先前状态的信息的时间比快速活动迹要长，因此对这两个迹的比较揭示了刺激强度最近是增加还是降低。这在图3C中的示例中进行了描述。在此，智能体在3 s, 9 s和15 s从状态x转到状态y，在6 s和12 s从y转到x。为了说明的目的，对网络进行初始化，以使V(y)的估计大于V(x)的估计：与y相关的状态-critic突触比与x相关的状态-critic突触更强。因此，当智能体从x转到y时，critic神经元发放率会增加，而当智能体从y转到x时会降低。由于快速活动迹比落后活动迹更快地适应突触后活动的变化，因此在x的状态-critic突触的可塑性间隔内，Λ^r大于Λ^l(请参见图3B)。相反，在y的状态-critic突触的可塑性间隔内，Λ^r小于Λ^l。Pfister and Gerstner (2006)在脉冲时序依赖可塑性(STDP)的背景下讨论了所有这三种活动迹的生物物理候选。因此，与离散时间算法1.3类似，我们可以对价值函数更新的连续公式进行以下分析：

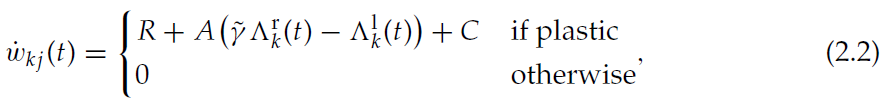
其中R是表示与连续状态相关的奖励的实值信号(请参阅第2.1节)，A和是系数，C是常数；可塑性条件由突触前活动迹决定(见公式2.1)。注意到，所有项都依赖于突触局部信息，但全局奖励信号R除外，该信号是不确定的(对于所有突触都是相同的)。一种可能的生物学方法是释放神经递质(如多巴胺)，多巴胺已被证明是皮质纹状体突触可塑性的第三个因素(有关综述，请参见Reynolds ＆ Wickens, 2002)。在这项研究中，我们不关心特定神经递质动态的复制，因此我们以最简单的方式实现奖励信号：如果智能体到达与奖励R相关的状态，则直到智能体离开状态，奖励信号R都有效。图3C中的示例显示了与低价值状态x相关的状态-critic突触的平均权重的发展。在此示例中，没有状态得到奖励(R = 0)。由于在与状态x相关的突触的可塑性间隔内与之差为正，表示x的神经元和critic之间的突触权重增加。相反，当智能体从y转到x时，可塑性间隔内与之差为负，这会导致代表y的神经元和critic之间的突触强度降低(数据未显示)。显然，这类似于公式1.3中定义的价值函数更新；两种公式的等效性所需的参数R，A和的选择在第3.1节中进行了说明。

　　我们的规则可以被认为是属于差分Hebbian学习规则的一类，后者取决于神经元活动的发放率，而不是像传统的Hebbian规则那样取决于同时的突触前和突触后活动。差分Hebbian规则由Klopf (1986)和Kosko (1986)引入，形式为——权重的变化与突触前和突触后发放率变化的乘积成正比。这样的规则可以解释经典条件(Klopf, 1988)。最近，另一种差分Hebbian规则的变体(权重的变化与突触前信号和输出信号的导数的相关性成正比)被成功地应用于RL控制问题(Porr ＆ Wörgötter, 2003, 2007; Wörgötter ＆ Porr, 2005)。在我们的规则中，权重的变化与突触后发放率的变化率成正比，这由两条活动迹和之差表示，但与突触前发放率的变化率无关。突触前发放率决定了突触何时是可塑的，而不是权重变化的大小；它的影响在微弱的意义上是倍增的。Roberts (1999)证明，在一定的约束下，实验观察到的STDP现象(Markram, Lübke, Frotscher, & Sakmann, 1997; Bi & Poo, 1998; Zhang, Tao, Holt, Harris, & Poo, 1998)暗示了差分Hebbian学习(从突触权重的平均变化与突触后脉冲概率的变化率成正比的意义上讲)。研究我们的规则在多大程度上与STDP或其他经验可塑性数据兼容，不在本研究范围内。

 

2.2.2 State-Actor Plasticity

　　状态和actor神经元之间的突触权重代表神经元actor-critic结构中的策略。在此，我们提出公式1.5给出的可塑性规则的生物学合理实现。类似于离散时间算法中的价值函数更新(公式1.3)，仅当刚刚选择相应的动作时，才更新偏好价值。在更新偏好价值的情况下，更新的大小与价值函数中的更新大小成比例(比较公式1.3和1.5)。在神经元框架中，这些属性可以解释如下：

1. 除了刚刚选择相应的动作外，状态-actor的突触可塑性几乎可以忽略不计。
2. 状态-actor突触更新与状态-critic突触更新成比例。

　　为了保证权重更新的正确时间，我们假设可塑性是由突触后活动控制的。状态神经元 j 和actor神经元 l 之间的突触是可塑的，而如公式2.1中所实现的具有时间常数τ_a的突触后活动迹超过阈值θ^a。对于足够高的θ^a值，仅在选择特定动作之后，才在actor神经元发放后的短时间内满足此条件(请参阅第2.1节)。为了满足比例标准，我们假设虽然突触是可塑的，但它受到状态神经元和critic神经元之间突触的增强或抑制的轴突异突触传播：

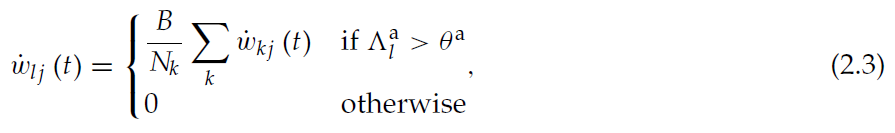
其中B是一个标量系数，N_k是每个状态神经元对critic神经元的突触数量，是神经元 j 和critic神经元k之间的突触权重的变化率，如公式2.2所定义。权重限制在30 fC至90 fC的范围内。连续权重更新类似于离散时间算法(公式1.5)中的偏好更新。从某种意义上说，它是局部的，因为它仅依赖于突触后脉冲和可用于突触前神经元轴突的信息。

　　在各种准备工作中已观察到轴突或突触前增强和抑制的传播。Bonhoeffer, Staiger, and Aertsen (1989)证明，如果在大鼠海马体切片培养物内的突触中诱导了长期增强(LTP)，则突触前神经元的其他轴突突触至少在150 μm范围内也可以观察到增强。在Kossel, Bonhoeffer, and Boltz (1990)中的大鼠视觉皮质, Schuman and Madison (1994)在300 μm范围内的急性海马体切片以及Bi and Poo (2000)中的稀疏培养海马体网络证实增强的突触前传播。Cash, Zucker, and Poo (1996)在非洲爪蟾的神经肌肉培养物中首次显示LTD的突触前传播，Fitzsimonds, Song, and Poo (1997)在大鼠海马体细胞的稀疏培养物中首次显示LTD。在这里，我们假设异突触可塑性的一种形式也取决于受影响的突触的突触后神经元的参与。支持这一点的证据是模棱两可的。在LTD的情况下，将神经元电压截断在-80 mV并不能防止其突触的异突触抑制(Fitzsimonds et al., 1997)，这表明不需要突触后神经元的参与。在LTP的情况下，电压截断这样的神经元-95 mV结合全细胞透析和Ca²⁺螯合确实抑制了其突触的异突触增强(Schuman ＆ Madison, 1994)，这表明确实需要突触后神经元的参与。相似形式的异突触可塑性已经被用来对延迟线拓扑的发展进行建模，该延迟线拓扑可以检测两个刺激之间的延迟(Kempter, Leibold, Wagner, & van Hemmen, 2001; Leibold, Kempter, & van Hemmen, 2001; Leibold & van Hemmen, 2002)。但是，在这些研究中，受影响突触的突触后神经元的活动以加性而非乘性方式调节突触权重。

3 Mapping Between Continuous and Discrete Time Update Rules

3.1 Value Function Mapping

　　公式2.2中表示的状态神经元和critic神经元之间的突触权重更新是由离散时间TD(0)算法(公式1.3)的价值函数更新启发式激发的。在本节中，我们显示了价值函数更新的连续时间和离散时间公式的等效性。

　　在神经元网络中，每个状态的价值由连接相应状态神经元池和代表critic的神经元池的突触集表示。当属于该集合的每个突触的权重变化略有不同时，我们考虑与状态s相关的状态-critic突触平均权重的动态变化：

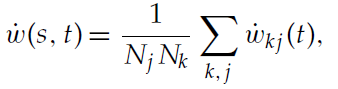
其中表示状态s的神经元 j 和critic神经元k之间的权重w_kj的动态由公式2.2给出，N_j是表示状态s的神经元数量，N_k是critic神经元的数量。可塑性间隔中平均突触权重的动态为：

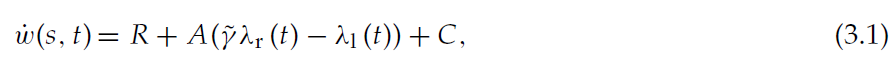
其中λ_r/l表示活动迹Λ^r/l的均值，可以通过对活动迹Λ^r/l的动态求均值来获得：

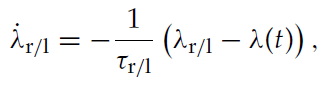
其中λ(t)表示突触后发放率。这个非齐次微分方程的解为：

为简单起见，当智能体处于状态s时，我们认为λ(t)是常数。如果智能体在时间t₀从s_i转到s_i+1，则critic神经元的发放率从λ(s_i)变为λ(s_i+1)，根据公式3.2，自适应发放率函数λ_r/l将突触后发放率的变化表示为：

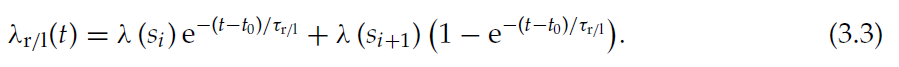
当智能体从s_i转到s_i+1时，与状态s_i相关的状态-critic突触在s_i离开后的短时间间隔Δt = t₂ - t₁(请参阅第2.2.1节)中是可塑的。根据公式3.1和3.3，在此时间间隔内，平均突触权重w(s_i, t)的总变化为：

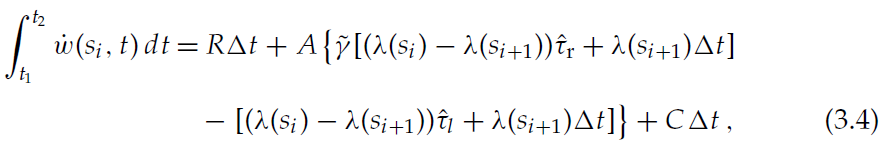
其中和。如2.2.1节所述，突触可塑性的时期Δt由突触前活动阈值θ_p和θ_l确定：t₁是突触前发放率达到较高阈值θ_p的时间，t₂是突触前发放率达到较低阈值θ_l的时间。这些时间可以通过以下公式计算得出：类似于公式3.3的公式来表示突触前发放率λ_s的发展，并分别求解λ_s = θ_p和λ_s = θ_l：

此处，λ_ac是处于活动状态的状态神经元的发放率，而λ_in是处于非活动状态的状态神经元的发放率。

　　为了在智能体移动后，将w(s_i)的总变化与公式1.3给出的V(s_i)的总变化进行比较，我们需要在突触权重单位和价值函数单位之间进行转换。因此，我们从两个线性变量转换开始：

其中λ(s_i)是对应于状态s_i的critic神经元的发放率。平均突触权重w与critic神经元的发放率λ之间的线性关系是权重较好的拟合(在30 fC至90 fC (mλ = 0.65 Hz/fC, cλ = -13.7 Hz)的范围内)。对于从λ到V的变换，我们要求V的极值在适当的权重范围内：V_min对应于w_min ≥ 30 fC，V_max对应于w_max ≤ 90 fC。V的极值完全由任务和γ值确定。因此，可以通过求解线性方程组来获得参数m_V和c_V，

用于特定任务。根据线性变量变换3.6和3.7转换为突触权重单位的离散时间价值函数更新规则1.3为：

其中

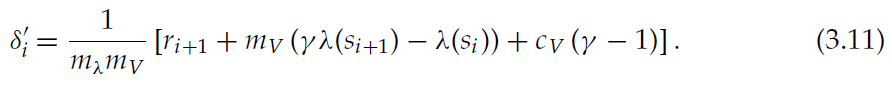
如果因连续时间更新而导致的突触权重总变化(公式3.4)与转换为突触权重单位的价值函数的离散时间更新相同，则价值函数更新的连续时间和离散时间公式都是等效的，公式3.10：

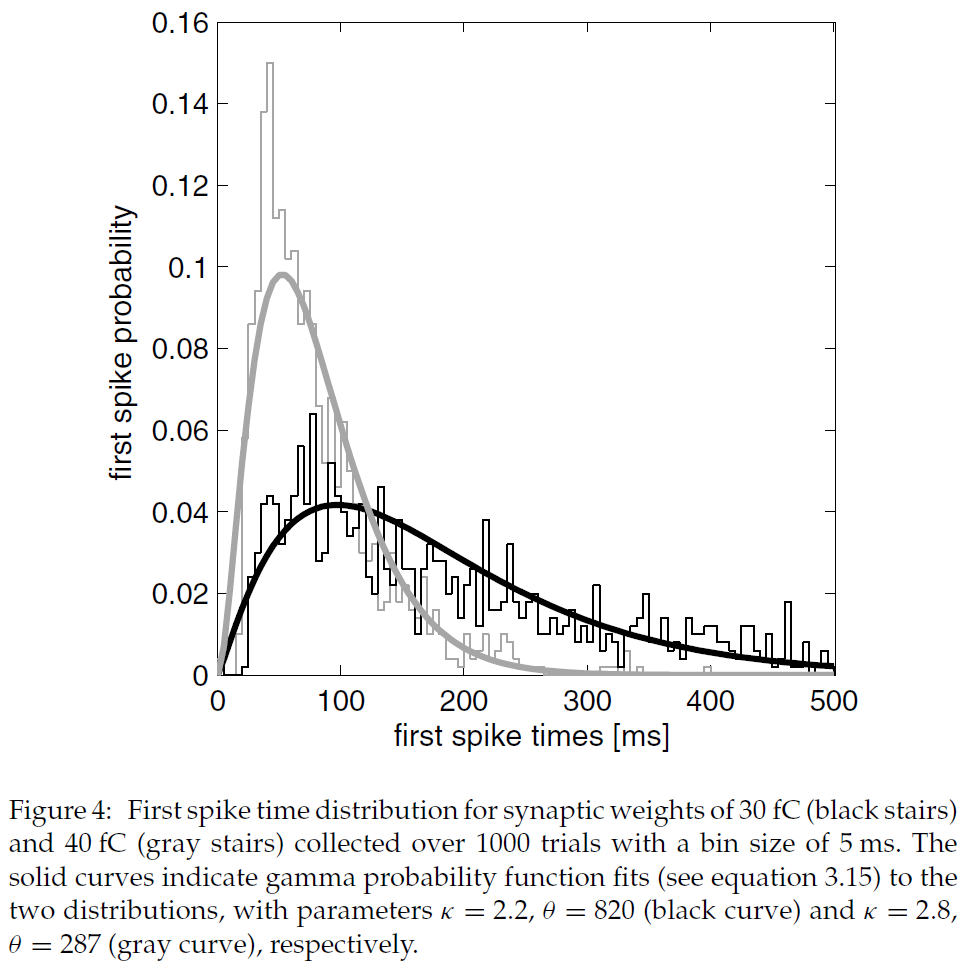
比较公式3.11和3.4中的系数会导致以下参数映射，从传统的TD(0)离散时间算法实现到连续时间神经元实现：

3.2 Policy Mapping

　　在本节中，我们证明状态与actor神经元之间的突触权重等效于TD(0)的离散时间算法实现的策略。如2.1节所述，在动作抑制周期之后首先发放的神经元确定该状态的选定动作。因此，智能体的策略π(s, a)等效于智能体处于状态s时actor神经元a首先发放的概率。当每个actor神经元从状态神经元收到相同的脉冲序列时，一个actor神经元首先发放的概率取决于其自身突触权重的强度以及其他竞争性actor神经元突触权重的强度。由于每个突触的权重变化略有不同，我们计算相对于平均突触强度选择特定动作的概率：，其中w_lj是状态神经元 j 和actor神经元 l 之间的突触强度，而N_j是状态s对应的神经元数量。假定传入神经元p和q的突触强度分别为w_p和w_q，则p在q之前发放的概率为：

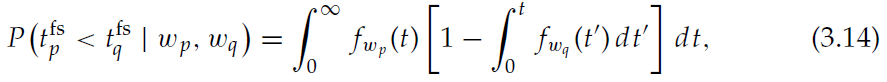
其中是相应神经元的初次脉冲时间，f_w(t)是强度为w的突触权重的神经元的初次脉冲时间分布。该表达式很容易扩展到两个以上的权重。为了获得解析表达式，我们可以使用gamma概率密度函数拟合经验性初次脉冲时间分布：

其中Γ为gamma函数。出于本研究的目的，我们确定了在30 fC和90 fC之间的突触强度的参数κ和θ，步长为1 fC，在40个突触上突触前发放率为42.63 Hz，对应于在激活条件下从状态神经元接收到的输入。图4显示了经验分布和相应拟合的两个示例。对于神经元q之前神经元p发放的概率，这产生以下表达式：

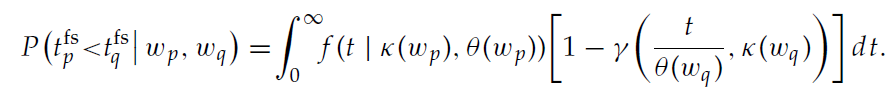
此处，γ(t, κ)是不完全的gamma函数，其中γ(t, κ) = 。由于公式3.14等价于在状态s中选择动作a(由神经元p表示)的概率π(s, a)，因此我们可以在TD(0)的神经元实现中定量比较在给定状态下采取给定动作的概率，以及通过离散时间算法实现学到的知识。

　　等式2.3中给出的状态-actor突触的可塑性动态暗示着权重变化与状态-critic突触的平均权重变化成正比，因此类似于等式1.5中给出的softmax动作选择方法的偏好更新。通过组合公式2.3和3.12，我们得到，其中β' = αB。但是，给定的权重变化在两种实现方式中不会在策略上产生相同的变化，因为上述神经元动作选择方法和softmax动作选择是不同的非线性函数。因此，两种实现方式中的参数β和β'相似但不相等。

4 Performance

4.1 Latency in a Gridworld Task

4.2 Accuracy of Mapping

4.3 Robustness to Parameters

5 Alternative Plasticity Rules Implementing TD Learning

　　在2.2.1和2.2.2节中，我们介绍了一组针对状态-critic和状态-actor突触的属性，这些属性保证了价值函数的实现和actor-critic TD(0)学习的策略更新。我们制定的特定可塑性规则的动机是将离散时间算法的属性尽可能准确地映射到连续时间可塑性机制。在本节中，我们放宽此约束，并考虑具有所描述属性的一些其他生物学合理的可塑性规则。

　　状态-critic神经元的第一个属性是，除了在智能体离开相应状态后的短时间内，它们的可塑性可忽略不计。为了满足该标准，我们引入了突触前活动迹(请参见公式2.1)，并使可塑性取决于经过某些阈值。作为替代时间机制，让我们考虑突触前功效迹ε_j，它在每个突触前脉冲都设为0，并以时间常数τ_ε指数恢复为1：

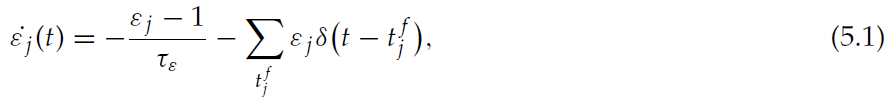
其中表示突触前神经元 j 的第 f 个脉冲。Froemke and Dan (2002)引入了这种迹，为STDP定义了一个模型，该模型考虑了从三重脉冲和四重脉冲协议获得的数据。现在，我们可以为状态-critic突触的可塑性定义一个替代的表述：

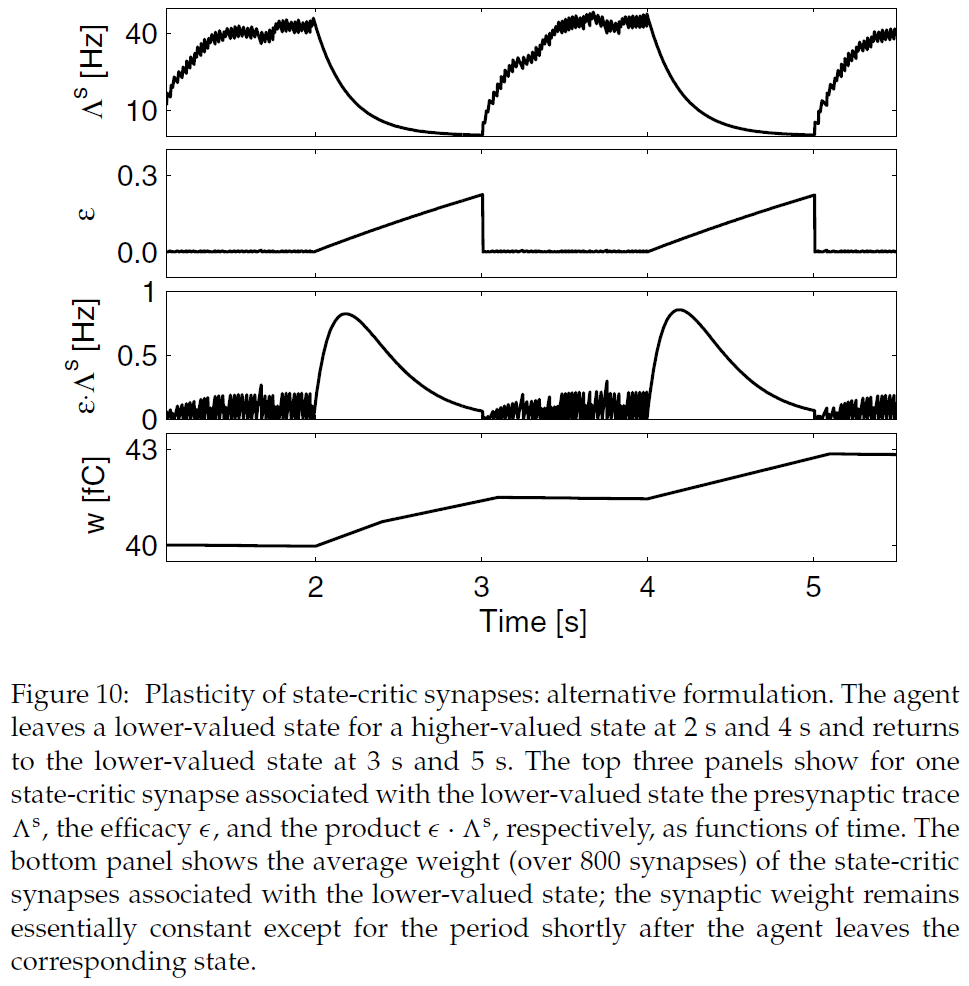
此规则的正确时间属性可以理解如下。在智能体到达状态之前，代表该状态的神经元受到的刺激很小，因此发放率极低。当智能体处于该状态时，突触前发放率很高，但是如果τ_ε比脉冲间隔长得多，则平均功效有效为0。乘积仅在智能体刚刚离开状态且功效恢复到1时才有意义。不可忽略的可塑性的时间间隔由突触前活动迹的衰减时间追溯到0。如果突触前活动迹的时间常数τ_s与τ_asp相比较小，则不可忽略的可塑性间隔足够短，以至于仅考虑一种状态转换。对于τ_ε = 4000 ms和τ_s = 200 ms，这在图10中进行了描述。

　　此可塑性规则不是TD(0)学习的严格实现，公式2.2，因为突触在整个过程中都是弱可塑性的。但是，如果我们假设智能体离开相应状态后，在时间间隔τ_asp之外的突触权重变化很小，则可以再次从TD(0)学习的离散时间价值函数更新的参数得出映射(见附录B)。我们在Gridworld任务(参见第4.1节)的仿真中测试了该突触可塑性规则的学习行为，其中τ_ε = 1000 ms, τ_s = 300 ms, τ_asp = 1000 ms, τ_l = 500 ms和τ_r = 0.5 · τ_l。对于离散时间TD(0)学习参数α = 0.4, γ = 0.9和r = 12 (cV = 0)，我们获得的突触可塑性参数A = 1.1 fC/Hz², = 0.98, R = 2.8 fC，并且C = 0 fC。在10次运行中，映射σ_V精度的平均度量(参见公式4.1)为2.1 fC，或V^dta(s)最大值的3.3％，4400步后的平均总奖励为774.2 ± 35.5(数据未显示)。这与通过公式2.2 (σ_V = 2.7 fC; 4400步后的平均总回报：769 ± 50.8)获得的可塑性规则所获得的性能相当。因此，由公式5.2给出的可塑性规则也代表了SNN中TD(0)学习的价值函数更新的生物学合理实现。该规则也可以被视为属于差分Hebbian规则的类别(请参阅第2.2.1节)；这次取决于突触前活动与突触后活动变化率之间的相关性。它与各向同性序列有序学习(Porr ＆ Wörgötter, 2003)和TD学习的非脉冲网络模型(Barto, 1995; Houk, Adams, ＆ Barto, 1995; Foster et al., 2000)中使用的规则非常相似。

　　状态-critic神经元的第二个属性是，它们对critic神经元的特征动态响应敏感。在第2.2.1节中，我们简单地假设critic神经元的发放率编码状态价值，并制定了一个对突触后发放率变化敏感的突触可塑性规则。但是其他动态响应也可以编码输入刺激变化，例如，在放松到新发放率之前的短暂发放率偏移(例如，Gazeres, Borg-Graham, & Frégnac, 1998; Muller, Buesing, Schemmel, & Meier, 2007)。

　　类似地，可以找到实现actor-critic策略更新的替代规则。状态-actor突触的第一个特性是它们的可塑性可忽略，除非刚刚选择相应的动作。我们通过使可塑性取决于突触后活动高于某个阈值来实现这一点。通过将权重更新规则(公式2.3)乘以突触后发放率，可以类似于公式5.2获得满足此时间标准的状态-actor更新规则的替代公式：

状态-actor突触更新规则的第二个属性是与状态-critic突触的更新成比例。这就意味着存在着一种不严格地局限性的机制，因为所需要的信息不能仅仅从突触前和突触后活动中获得。这是actor-critic架构的模块化结构的代价。通过假定突触变化沿状态神经元的轴突传播，我们直接在公式2.3中实现了这一点。但是，状态-critic突触的更新取决于critic神经元的动态响应。因此，另一种方法是假设critic神经元投射到状态-actor突触并影响其可塑性，这是神经调节性第三因素，如多巴胺用于皮质纹状体突触的情况已证实(综述见Reynolds ＆ Wickens, 2002)。

6 Discussion

　　在这项研究中，我们证明了脉冲神经元网络可以实现actor-critic的TD学习智能体。为此，我们导出了一个映射，该映射允许离散时间算法由连续时间运行的脉冲耦合动态系统执行。与传统的离散时间算法一样，智能体在离散状态空间中移动并采取离散动作。但是，许多有趣的现实世界问题(例如学习如何接球)无法轻易地简化为这样的框架。一旦证明可以实现这种简单的情况，下一步自然就是要扩展网络模型，以便能够解决连续的时空任务。例如，在Munos (2006)和Doya (2000b)中已经提出了针对连续时间问题的非脉冲算法。我们研究了actor-critic方法，而不是像REINFORCE算法这样仅有actor的方法，因为后者依赖于频繁的奖励，而许多现实世界中的问题却具有稀疏，延迟且不可靠的奖励(Williams, 1992; Seung., 2003)。actor-critic的基础是，critic产生内部奖励，即使没有外部奖励，actor也可以调整其策略。这种分工使actor-critic能够解决时序信度分配问题，即使对于奖励稀疏的任务也是如此，例如在这里以Gridworld为例。我们根据动作价值(例如Sarsa和Q学习)(参见Sutton ＆ Barto, 1998)来研究actor-critic方法，而不是TD学习方法(因为Sutton & Barto, 1998)，由于actor-critic结构的模块化布局已经提出了适当的网络结构，它也能够学习奖励稀疏的任务。确实，有实验证据支持一种actor-critic范式，在这种范式中，大脑的不同区域都扮演着actor和critic的角色(O'Doherty et al., 2004; Tricomi, Delgado, & Fiez, 2004)。actor-critic结构的模块化结构也启发了对基底神经节的众多理论研究(Barto, 1995; Houk et al., 1995; Suri & Schultz, 1999; 有关最新综述，请参见Joel, Niv, & Ruppin 2002)。但是，最近的证据也支持其他TD学习模式，例如基于动作价值的模式(Morris, Nevet, Arkadir, Vadia, & Bergman, 2006)或actor/director模型(Attalah, Lopez-Paniagua, Rudy, & O'Reilly, 2007; Lerchner, La Camera, ＆ Richmond, 2007)，因此需要进一步研究这些技术的神经元实现。

　　在此，我们重点研究了能够实现一种特定算法以进行系统级学习的神经机制，但我们并不声称这是大脑使用的算法。确实，大脑似乎有可能根据要解决的问题采用各种学习策略。大脑的各个部分都与不同类别的学习相关联，例如，小脑的监督学习，基底神经节的强化学习和大脑皮层的无监督学习(参见综述Doya, 2000a)。大脑还可能使用尚未形式化的策略组合。

　　强化学习经常被批评为花费太长时间而无法收敛到生物学目的。在我们的示例中，智能体需要大约100次尝试才能学习任务。但是，此任务比最初看起来要困难得多，因为智能体没有有关基础网格状结构的信息。考虑以下思想实验。为你提供一张带有易于识别图像的卡，例如游戏存储器中使用的卡。你可以选择1到4之间的数字，这时(确定地)将卡替换为另一张卡。你可能会继续选择号码，直到找到带有甜甜圈照片的卡片，然后你才能获得奖励。然后，你从随机卡再次开始。在我们实验室中使用这种设置进行的非正式实验表明，即使受试者知道每张卡都已分配到网格上的某个位置，并且每张号码都已分配给了该卡，也很难学习快速获得奖励卡的方法。如果将基本问题结构的知识并入算法中，例如导航任务中空间的连续性，则通过强化学习技术可以更快地收敛，这可以通过强化学习技术来实现(Foster et al., 2000)。但在某些方面，由于智能体对其状态和策略有全面的了解，因此任务也比看起来容易得多。它不会造成任何识别错误，而作者有时会将其办公楼的二楼误认为三楼，并且没有执行错误，而作者却知道他们居住在日本，但在过马路时仍然会走错路。强化学习的基本形式的另一个局限性是学习智能体是纯粹反应性的。一旦学习稳定，智能体在每次出现时对给定刺激将具有相同的概率响应。这反映在我们模型的前馈结构中。更先进的系统将能够由于自身的动态(例如，由于动机或注意力)而在不同的内部状态之间切换，从而对相同的刺激产生不同的概率响应。

　　我们已经表明，具有生物学现实的脉冲发放率的合理的小型网络可以执行必要的计算，以在200毫秒之内更新其价值函数和策略。这似乎与生存所需的反应时间兼容。由于对于少于200毫秒的响应时间，突触级别的信息很少，因此无法通过增加网络中神经元的数量来改进网络的性能。就活动迹的时间常数而言，即使在τ_r接近0或τ_l的极限情况下，网络的性能也很稳定。在所有实验中，都仔细选择了参数A，，C和R(请参阅附录A)，这可能给人的印象是系统对参数选择高度敏感。实际上，对参数的谨慎选择是由与离散时间算法实现等效性的要求所激发的。网络以与传统离散时间算法可以解决一系列参数α和γ相同的方式学习广泛的参数。这就提出了一个问题，即鉴于不同的参数对于不同的任务而言是最优的，大脑如何确定这些参数。大脑是采用一套"足够好"的参数还是通过元可塑性来学到适当参数(Doya, 2002)？这个问题只能通过精心设计的行为学实验来解决。

　　我们的模型依赖于两种特殊类型的突触可塑性：critic模块中的差分Hebbian和actor模块中的异突触轴突可塑性。在实验和理论文献中都讨论了这两种机制的各个方面，但是这里没有直接证据证明权重动态的完整形式。critic模块的可塑性是局部的，仅取决于突触前和突触后的脉冲，除了它对编码奖励的全局信号敏感之外。可以通过在一定间隔内刺激突触前和突触后神经元对以使其以恒定发放率激发来实现揭示这种可塑性的实验装置。在间隔结束时，应停止突触前刺激，同时增加或降低突触后刺激的强度。对第2.2.1节中提出的可塑性规则的预测是，在同时刺激过程中，突触强度保持恒定，然后根据是否增加或减少突触后刺激而进行增强或抑制。actor模块的可塑性是局部的，因为它取决于突触后的活动，但也取决于突触前神经元轴突可获得的信息，严格来说，这不是局部的。对2.2.2节中提出的规则的实验预测是，如果各自的突触后神经元处于活跃状态，则长期增强和长期抑制的轴突扩散对突触的影响要大得多。但是，第5节中讨论的actor模块的另一种可塑性是，critic模块的输出直接影响状态-actor，作为神经调节的第三因素。在这种情况下，实验预测是，当最近有突触前和突触后活动时，这种突触会发生最大的变化，并且神经调节剂的瞬时增加会诱导增强，而瞬时的下降会引起抑制。神经调节性第三因素的明显候选是多巴胺。在进一步的工作中，我们将调查此处假设的可塑性规则在多大程度上与成熟的突触可塑性机制兼容或可以被其替代。

　　此处执行的动作选择机制非常简单，而且非常脆弱：如果代表西方的神经元死亡，该智能体将永远无法再次向西方走。但是，很容易想到扩展网络以包含更强大的动作选择机制，例如通过吸引子网络(Amit, 1989)，竞争性同步发放链(Hayon, Abeles, & Lehmann, 2004)或动作群体基于发放率的编码(Georgopoulos et al., 1982)。

　　这项工作的一个有趣的技术方面是，我们采用了离散的串行算法，并在连续时间内利用细粒度的并行性对其进行了重新格式化。在我们的模型中，没有中央实例来调整价值函数和策略。突触会根据自身的动态将自身调整为适当的值。对生物基质的细粒度并行性采用标准算法并不能立即为我们带来实际优势。如果在标准硬件上模拟生物基质，则其效率可能不如直接实现标准算法。但是，正在进行大量研究来创建硬件来模拟神经组织的功能，主要是FPGA和模拟VLSI (Guerrero-Rivera, Morrison, Diesmann, & Pearc, 2006; Philipp, Grubl, Meier, & Schemmel, 2007)。基本的问题已经解决，但是神经元和突触的数量仍然存在局限性。 一旦这些技术能够生产出具有适当数量的神经元和突触的设备，它们便可以充分利用像本文开发的那样的微观并行算法，并以至少与自然大脑相同的速度和精度解决问题。但是，几乎与标准计算机一样，这些设备是通用引擎，需要进行编程以解决特定任务。因此，从技术角度来看，这项工作也可以解释为对即将到来的神经形态硬件的神经元软件的探索。

Appendix A: Parameters and Simulation

Appendix B: Value FunctionMapping for an Alternative Plasticity Rule