郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

CoRR, (2019)
Abstract
通常,从有限的一组选项中试探性地选择损失函数,正则化机制和训练参数模型的其他重要方面。在本文中,我们将朝着使该过程自动化的第一步迈进,以期产生能够更快且更强大的训练模型。具体而言,我们提出了一种用于学习参数损失函数的元学习方法,该方法可以推广到不同的任务和模型架构中。我们开发了一条用于"元训练"损失函数的流水线,旨在最大程度地提高在其下训练的模型性能。在监督学习和RL任务中,我们的学习损失所产生的损失态势显著提高了特定于任务的原始损失。此外,我们证明了我们的元学习框架足够灵活,可以在元训练时合并其他信息。此信息可影响学习到的损失函数,从而使环境无需在元测试时间内提供此信息。
1. Introduction
受人类快速学习和适应新任务的非凡能力的启发,学会学习或元学习的概念最近在机器学习社区中变得流行(Andrychowicz et al., 2016; Duan et al., 2016; Finn et al., 2017)。我们可以将学会学习方法大致分为两类:可以概括并易于适应新任务的表征学习方法(Finn et al., 2017),以及学会如何优化模型的方法(Andrychowicz et al., 2016; Duan et al., 2016)。
在本文中,我们研究了第二种方法。我们提出了一个学习框架,该框架能够学习任何参数化损失函数,只要其输出相对于参数可微即可。这样学到的函数可用于有效地优化新任务的模型。
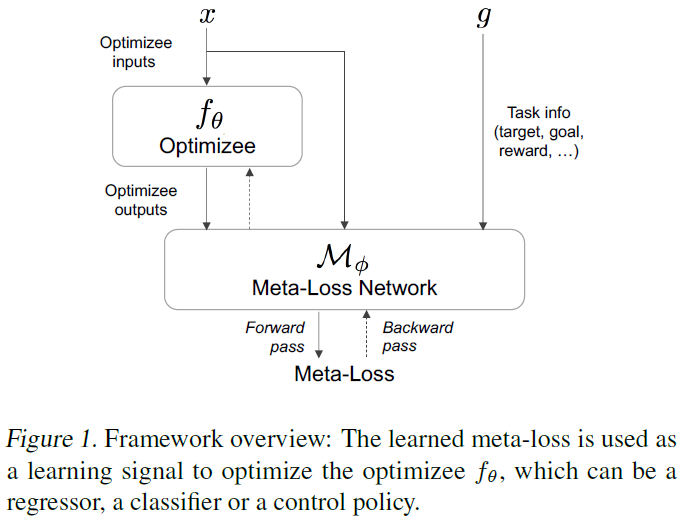
具体来说,这项工作的目的是将学习策略编码为概括多个训练上下文或任务的参数化损失函数或元损失。受到逆强化学习(Ng et al., 2000)的启发,我们的工作将元学习的学会学习范式与学习损失态势的一般性结合起来。我们构建了一个统一且完全可微的框架,该框架可以学习独立于优化对象的损失函数,从而为分类,回归或RL等各种学习问题提供强大的学习信号。我们的框架涉及内部和外部优化循环。在内环中,使用从我们学到的元损失函数产生的损失,通过梯度下降训练模型或优化对象。图1显示了用于使用元损失更新优化对象的流水线。外环通过最小化由更新的优化对象引起的任务损失(例如标准回归或RL损失)来优化元损失函数。
这项工作的贡献如下:i)我们提出了一个用于通过反向传播学习自适应高维损失函数的框架,该函数创建了损失态势以进行梯度下降的有效优化。我们证明,我们所学习的元损失函数相对于直接通过任务损失本身进行学习有所改进,同时又保持了任务损失的一般性。ii)我们提出了几种框架可以整合额外信息的方式,这些信息可以帮助在元训练时塑造损失态势。这些额外的信息可以采取各种形式,例如探索性信号或RL任务的专家演示。在训练了元损失函数之后,不再需要特定于任务的损失,因为可以完全通过单独使用元损失函数来执行优化训练,而无需在元训练时给出额外的信息。这样,我们的元损失可以找到更有效的方法来优化原始任务损失。
我们将元学习方法应用于各种问题,这些问题证明了我们框架的灵活性和通用性。这些问题包括回归问题,图像分类,行为克隆,有模型和无模型RL。我们的实验包括对上述每个问题的经验评估。
2. Related Work



与我们的方法最接近的是关于进化策略梯度(Houthooft et al., 2018),教师网络(Wu et al., 2018),元critics(Sung et al., 2017)和元梯度RL(Xu et al. 2018)的工作。与使用进化方法(例如Houthooft et al., 2018)相反,我们设计了一个可微的框架并描述了一种在监督学习和RL环境中使用梯度下降优化损失函数的方法。Wu et al. (2018)提出,教师网络要被训练以预测手动设计的损失函数的参数,而不是直接学习可微的损失函数,并且每个新的损失函数类都需要新的教师网络设计和训练。在Xu et al. (2018)中,可以在线学习折扣和自举参数来优化特定于任务的元目标。我们的方法不需要手动设计损失函数参数化或选择必须优化的特定参数,因为我们的损失函数是完全从数据中学到的。最后,在Sung at al. (2017)的工作中元critic学习提供任务条件价值函数,该函数用于训练actor策略。尽管像在我们的工作中那样,在有监督的条件下训练元critic减少了学习损失函数的能力,但在RL环境中,我们证明了可以使用学到的损失函数直接通过梯度下降来优化策略。
1 对于简单的梯度下降:![]()

3. Meta-Learning via Learned Loss
在这项工作中,我们旨在学习损失函数(我们称其为元损失),然后将其用于训练优化程序,例如分类器,回归器或控制策略。更具体地讲,我们旨在学习带有参数Φ的元损失函数MΦ,该函数输出损失值Llearned,该值用于通过梯度下降训练带有参数θ的优化对象fθ:

其中y可以是监督学习设置中的真实目标信息,也可以是RL设置中的目标和状态信息。简而言之,我们旨在学习如算法2中所述的损失函数。针对这一目标,我们提出了一种通过梯度下降来学习元损失函数参数Φ的算法。
关键的挑战是推导出训练信号以学习损失参数。在下文中,我们描述了应对挑战的方法,我们称其为Meta-Learning via Learned Loss (ML3)。
3.1. ML3 for Supervised Learning



2 或者,可以使用自动微分执行此梯度计算
3.2. ML3 Reinforcement Learning
在本节中,我们介绍一些修改,这些修改使我们可以将ML3框架应用于RL问题。设M =(S, A, P, R, p0, γ, T)为有限步马尔可夫决策过程(MDP),其中S和A为状态和动作空间,P:S x A x S → R+是状态转换概率函数或系统动态,R:S x A → R是奖励函数,p0:S → R+是初始状态分布,γ为奖励折扣因子,T为时间范围。令τ = (s0, a0, ... , sT, aT)是状态和动作的轨迹,![]() 是轨迹回报。RL的目标是找到策略πθ(a|s)的参数θ,该参数可使该策略所引起的轨迹上的期望折扣奖励最大化:
是轨迹回报。RL的目标是找到策略πθ(a|s)的参数θ,该参数可使该策略所引起的轨迹上的期望折扣奖励最大化:![]() 中s0 ~ p0,st+1 ~ P(st+1|st, at)且at ~ πθ(at|st)。在接下来的内容中,我们将展示如何在RL方案中训练元损失网络以执行有效的策略更新。为了应用我们的ML3框架,我们将上一节中的优化对象fθ替换为随机策略πθ(a|s)。我们介绍了ML3到RL的两个应用。
中s0 ~ p0,st+1 ~ P(st+1|st, at)且at ~ πθ(at|st)。在接下来的内容中,我们将展示如何在RL方案中训练元损失网络以执行有效的策略更新。为了应用我们的ML3框架,我们将上一节中的优化对象fθ替换为随机策略πθ(a|s)。我们介绍了ML3到RL的两个应用。
3.2.1. ML3 FOR MODEL-BASED REINFORCEMENT LEARNING
有模型RL(MBRL)尝试通过首先学习动态模型P来学习策略πθ。直观地讲,如果模型P是准确的,我们可以使用它来优化策略参数θ。由于我们通常不知道动态模型是先验的,因此MBRL算法会在使用当前近似动态模型P进行迭代之间进行优化,以优化策略πθ,使其在P下最大化奖励R,然后使用优化后的策略πθ收集更多数据。在这种情况下,我们旨在学习损失函数,该函数用于通过我们的元网络M优化策略参数。
类似于监督学习设置,我们使用当前元参数Φ在当前动态模型P下优化策略参数θ:![]() ,其中τ = (s0, a0, ... , sT, aT)是采样的轨迹,变量g捕获一些特定于任务的信息,例如智能体的目标状态。为了优化Φ,我们再次需要定义一个任务损失,在MBRL设置中可以将其定义为
,其中τ = (s0, a0, ... , sT, aT)是采样的轨迹,变量g捕获一些特定于任务的信息,例如智能体的目标状态。为了优化Φ,我们再次需要定义一个任务损失,在MBRL设置中可以将其定义为![]() ,表示在当前动态模型P下获得的奖励。为了更新Φ,我们计算关于Φ的任务损失LT的梯度,这涉及通过奖励函数,动态模型和使用元损失MΦ更新的策略来进行完全微分。算法3(附录A)中的伪代码说明了MBRL学习循环。在算法5(附录A)中,我们显示了元测试期间的策略优化过程。值得注意的是,我们发现在实践中,不再需要动态的模型P来进行元测试时的策略优化。元网络学习隐式表示动态模型的梯度,并且会产生损失,无法直接优化策略。
,表示在当前动态模型P下获得的奖励。为了更新Φ,我们计算关于Φ的任务损失LT的梯度,这涉及通过奖励函数,动态模型和使用元损失MΦ更新的策略来进行完全微分。算法3(附录A)中的伪代码说明了MBRL学习循环。在算法5(附录A)中,我们显示了元测试期间的策略优化过程。值得注意的是,我们发现在实践中,不再需要动态的模型P来进行元测试时的策略优化。元网络学习隐式表示动态模型的梯度,并且会产生损失,无法直接优化策略。
3.2.2. ML3 FOR MODEL-FREE REINFORCEMENT LEARNING
最后,我们考虑了无模型RL(MFRL)的情况,此时我们学习策略而不学习动态模型。在这种情况下,我们可以定义一个独立于动态模型的替代目标,作为我们特定于任务的损失(Williams, 1992; Sutton et al., 2000; Schulman et al., 2015):
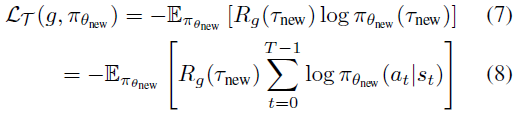
与MBRL情况类似,任务损失间接取决于用于更新策略参数的元参数Φ。尽管我们正在评估完整轨迹奖励的任务损失,但是我们根据等式2执行策略更新(在具有批量为B的小批量经验(si, ai, ri) (i ∈ {0, ... , B-1})的元损失上使用随机梯度下降(SGD),类似于Houthooft et al. (2018))。元损失网络的输入是采样状态,采样动作,任务信息g和采样动作的策略概率:MΦ(s, a, πθ(a|s), g)。通过这种方式,我们仅使用基于轨迹的奖励就可以使用SGD有效地优化超高维策略。与上面的MBRL设置相反,用于任务损失评估的部署是实际系统部署,而不是仿真部署。在测试时,我们使用与MBRL设置相同的策略更新过程,参见算法5(附录A)。
3.3. Shaping ML3 loss by adding extra loss information during meta-train
到目前为止,我们已经讨论了使用标准任务损失(例如MSE损失)进行回归分析或奖励函数用于RL设置。但是,有可能在元训练时提供有关任务的更多信息,这可能会影响对损失态势的学习。我们可以设计任务损失以纳入额外的惩罚;例如,我们可以使用Lextra扩展MSE损失,并使用β和γ对项进行加权:
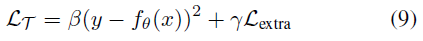
在我们的工作中,我们在元训练时尝试了4种不同类型的额外损失信息:对于监督学习,我们表明通过Lextra = (θ - θ*)2添加额外的信息,其中θ*是最优回归参数,帮助塑造凸损失态势,解决非凸优化问题;我们还展示了如何在机器人模型学习中使用Lextra以产生物理先验。对于RL任务,我们证明,通过在元训练时间内为任务损失提供额外的奖励,我们可以鼓励受过训练的元损失学习探索行为。最后,对于RL任务,我们将展示如何结合专家演示来学习可推广到新任务的损失函数。在所有设置中,额外信息都会影响学习到的损失函数,从而使环境无需在元测试时间内提供此信息。
4. Experiments
在本节中,我们从两个不同的角度评估所学到的元损失的适用性和收益。首先,我们在第4.1节中研究了使用标准任务损失(例如MSE损失进行回归)来训练元损失的好处。我们从泛化属性和收敛速度方面分析了学到的元损失与标准任务损失的比较。其次,我们在第4.2节中研究了在元训练时间添加额外信息以塑造损失态势的好处。
4.1. Learning to mimic and improve over known task losses
首先,我们分析了我们的元学习框架在监督学习和RL设置下如何学会模仿和改进标准任务损失。对于这些实验,通过一个神经网络对元网络进行参数化,该神经网络具有两个分别包含40个神经元的隐含层。
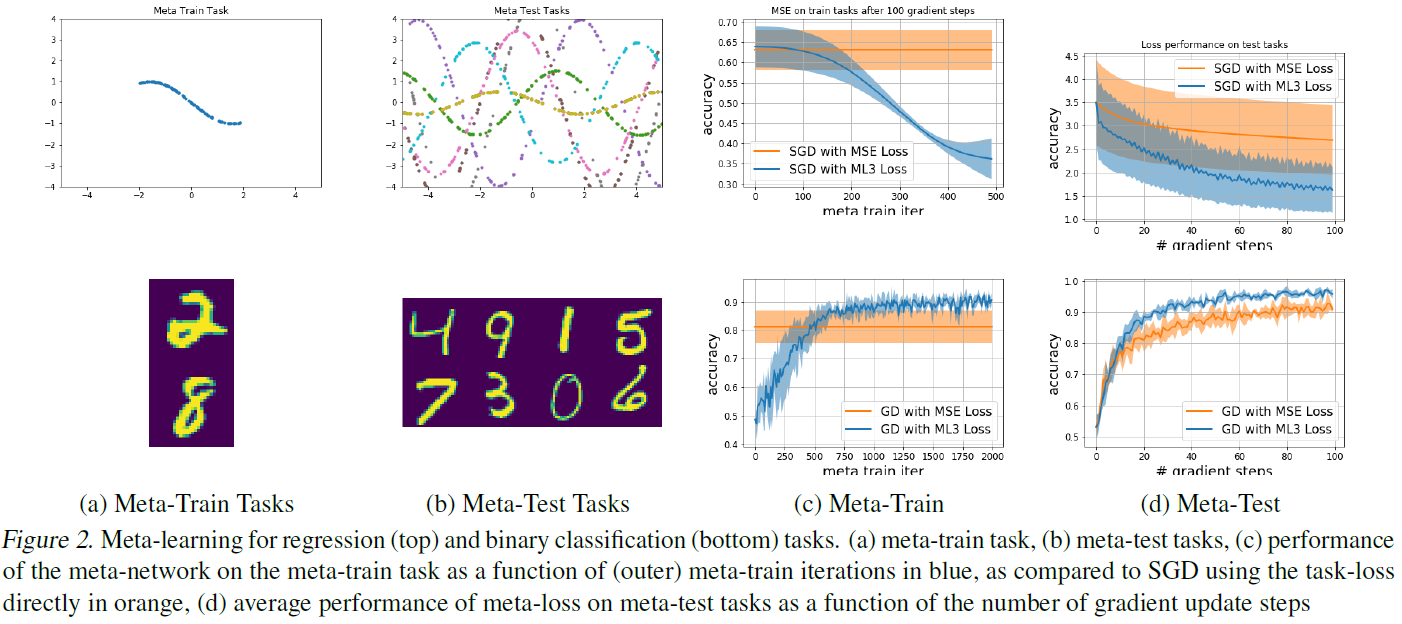
4.1.1. META-LOSS FOR SUPERVISED LEARNING



4.1.2. LEARNING REWARD FUNCTIONS FOR MODEL-BASED REINFORCEMENT LEARNING
在MBRL示例中,任务包括2D空间中点质量的自由运动任务(我们将此环境称为PointmassGoal)和带有2-链接2D机械手的到达任务(我们称其为ReacherGoal环境)(请参阅附录B中的详细信息)。任务分布p(T)由点质量或臂应到达的不同目标位置组成。在元训练时间内,从当前最优策略的样本中学习以神经网络为代表的系统动态模型。当在动态模型P中推出![]() 时,元训练期间的任务损失为
时,元训练期间的任务损失为![]() ,其中R(τ)是距目标g的最终距离。采用梯度
,其中R(τ)是距目标g的最终距离。采用梯度![]() 需要通过学到的模型P进行微分(请参阅附录3)。元网络的输入是当前部署和所需目标位置的状态-动作轨迹。元网络输出损失信号以及学习率以优化策略。图3a显示了在对PointmassGoal进行元测试期间,通过元损失优化的策略的定性到达性能。元损失网络仅针对x,y平面的右象限(蓝色轨迹)中的任务进行训练,并针对左象限(橙色轨迹)中的任务进行测试显示了元损失的泛化能力。图3b和3c显示了在测试时到目标位置的最终距离方面的比较。将经过元损失训练的策略的性能与经过任务损失训练的策略(在这种情况下,是到目标的最终距离)进行比较。曲线显示了10个不同目标位置的结果(包括需要概括元损失的目标位置)。在优化任务损失时,我们使用在元训练时间内学到的动态模型,因为在这种情况下,需要在测试期间通过模型进行微分。如3.2.1节所述,使用元损失时不需要这样做。
需要通过学到的模型P进行微分(请参阅附录3)。元网络的输入是当前部署和所需目标位置的状态-动作轨迹。元网络输出损失信号以及学习率以优化策略。图3a显示了在对PointmassGoal进行元测试期间,通过元损失优化的策略的定性到达性能。元损失网络仅针对x,y平面的右象限(蓝色轨迹)中的任务进行训练,并针对左象限(橙色轨迹)中的任务进行测试显示了元损失的泛化能力。图3b和3c显示了在测试时到目标位置的最终距离方面的比较。将经过元损失训练的策略的性能与经过任务损失训练的策略(在这种情况下,是到目标的最终距离)进行比较。曲线显示了10个不同目标位置的结果(包括需要概括元损失的目标位置)。在优化任务损失时,我们使用在元训练时间内学到的动态模型,因为在这种情况下,需要在测试期间通过模型进行微分。如3.2.1节所述,使用元损失时不需要这样做。
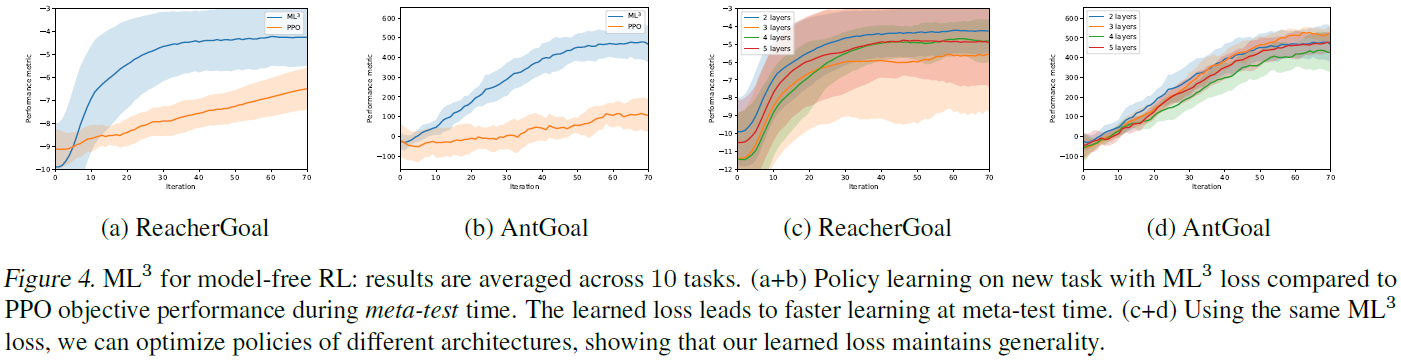
4.1.3. LEARNING REWARD FUNCTIONS FOR MODEL-FREE REINFORCEMENT LEARNING
在下文中,我们转向评估无模型RL任务。图4显示了使用基于OpenAI Gym MuJoCo环境(Gym, 2019)的两个连续控制任务时的结果:ReacherGoal和AntGoal(详细信息请参见附录C)3。图4a和图4b显示了元测试时间分别针对ReacherGoal和AntGoal环境的性能结果。我们可以看到,与PPO相比,在这两种情况下ML3损失都显著提高了优化速度。在我们的实验中,我们观察到,就无模型任务的指标而言,ML3达到80%的任务性能所需的样本量要平均少5倍。
为了测试元损失在不同结构上的泛化能力,我们首先在具有两层的结构上进行元训练MΦ,然后在层数不同的结构上对相同的元损失进行元测试。图4(c+d)显示了针对四种不同模型架构的无模型设置中ReacherGoal和AntGoal环境的元测试时间比较。每条曲线显示每种环境中十个不同任务的均值和标准差。我们的比较清楚地表明,与相应任务优化的总体方差相比,在性能稍有变化的情况下,元损失可以在多个结构之间有效地重复使用。
3 我们的框架是使用开放源代码库Higher (Grefenstette et al., 2019)实现的,用于方便的二阶导数计算,以及使用Hydra (Yadan, 2019)来简化实验配置的实现。
4.2. Shaping loss landscapes by adding extra information at meta-train time
这组实验表明,我们的元学习器能够学习损失函数,这些函数包含仅在元训练时间内可用的额外信息。学到的损失将被塑造,使得与标准损失相比,使用元损失时优化速度更快。
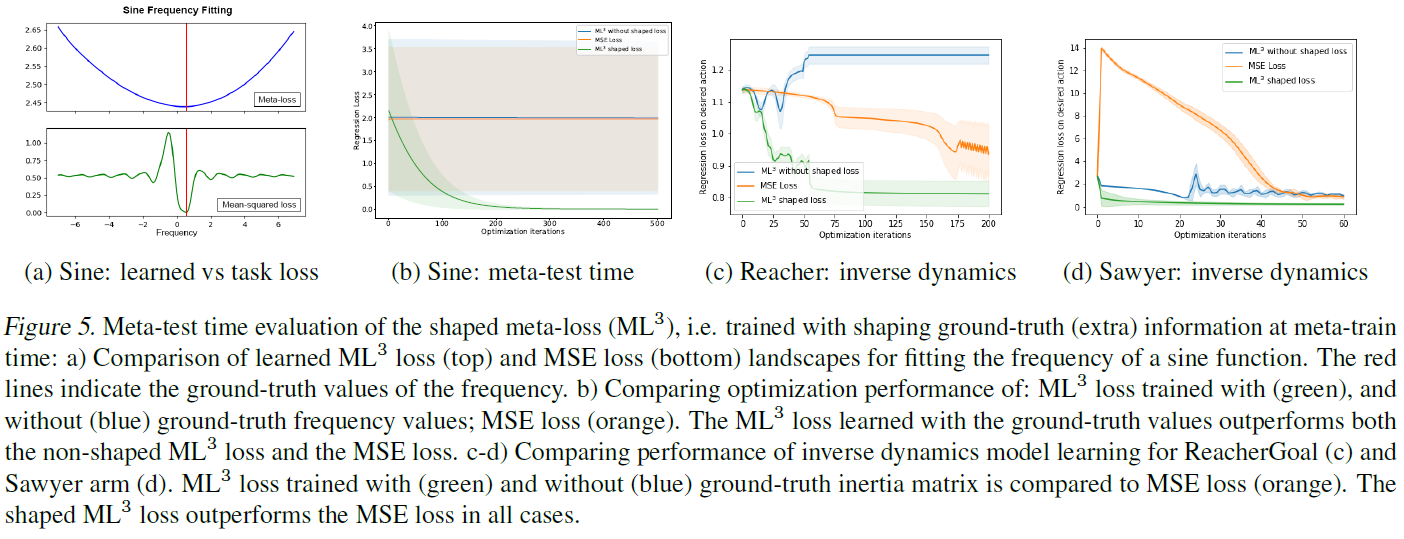
4.2.1. ILLUSTRATION: SHAPING LOSS
我们首先对正弦频率回归的例子塑造的损失进行可视化,其中为了简化可视化,我们拟合了一个参数。


4.2.2. SHAPING LOSS VIA PHYSICS PRIOR FOR INVERSE DYNAMICS LEARNING


4.2.3. SHAPING LOSS VIA INTERMEDIATE GOAL STATES FOR RL
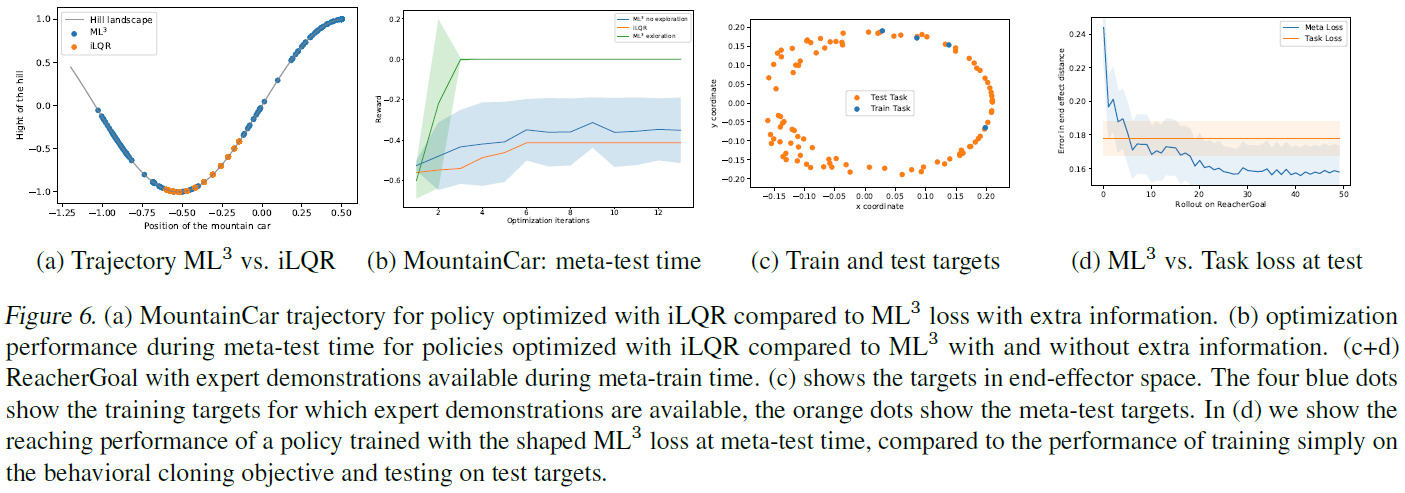
我们分析了MountainCar环境下的损失态势塑造(Moore, 1990),这是一个经典的控制问题,在这种情况下,驱动不足的车必须驶上陡峭的山坡。车产生的推进力不允许稳定爬坡,因此,贪婪地最小化到目标的距离通常会导致无法解决任务。状态空间是由车的位置和速度组成的二维空间,动作空间是由一维扭矩组成。在我们的实验中,我们在元训练时间内提供了中间目标位置,在元测试时间内无法提供这些目标位置。正如(图6-a)所示,与基于经典iLQR的轨迹优化(Tassa et al., 2014)相比,元网络将这种行为纳入其损失中,从而导致元测试期间的探究性提高。图6-b显示了在带有和不带有额外信息和iLQR的ML3策略更新的几次迭代中,车与目标之间的平均距离。正如我们所观察到的,带有额外信息的ML3可以通过少量更新就成功地将车带入目标,而没有额外信息的iLQR和ML3则无法解决此任务。
4.2.4. SHAPING LOSS VIA EXPERT INFORMATION DURING META-TRAIN TIME


5. Conclusions
在这项工作中,我们提出了一个框架,可以完全从数据中元学习损失函数。我们展示了如何使元学习到的损失变得良好,并适合于梯度下降的有效优化。当使用学到的元损失时,我们观察到回归,分类和基准RL任务的速度显著提高。此外,我们表明,通过在训练期间引入其他指导信息,我们可以训练元损失,以开发可显著提高元测试期间性能的探索性策略。
我们相信ML3框架是整合以前的经验并将学习策略转移到新任务的强大工具。在未来的工作中,我们计划着眼于结合多个学习到的元损失函数,以便概括不同的任务族。我们还计划进一步发展在训练期间引入额外好奇心奖励的想法,以改进因元损失而学到的探索策略。

A. MFRL and MBRL algorithms details
我们注意到实际上,在元损失输入中直接包括了策略的分布参数,例如高斯策略的均值μ和标准差σ比包括概率估计πθ(a|s)更好,因为它提供了直接的方法,可以通过元损失使用反向传播来更新分布参数。
B. Experiments: MBRL

C. Experiments: MFRL
ReacherGoal环境是2-链接2D机械手,必须使用其末端执行器到达指定的目标位置。任务分布(在元训练和元测试时间)由初始链接配置和机械手可及范围内的随机目标位置组成。此环境的性能指标是到目标的负距离的平均轨迹总和,是10项任务的均值。作为任务损失的轨迹奖励Rg(τ)(请参见等式7),我们使用Rg(τ) = -d+1/(d+0.001) - |at|,其中d是末端执行器到指定为二维笛卡尔位置的目标g的距离。该环境具有11个维度,用于指定每个链接的角度,从末端执行器到目标的方向,目标的笛卡尔坐标和末端执行器的笛卡尔速度。
AntGoal环境需要四足智能体才能运行到目标位置。任务分布由随机目标组成,这些目标在围绕初始位置的圆上初始化。此环境的性能指标是到目标的初始距离和当前距离之间的平均轨迹差之和,是10个任务的均值。与之前的环境类似,我们使用Rg(τ) = -d+5/(d+0.25) - |at|,其中d是从生物躯干中心到指定为2D直角坐标位置的目标g的距离。与ReacherGoal相比,此环境具有33维状态空间4,该状态空间描述了笛卡尔的位置,速度和躯干的方向以及所有八个关节的角度和角速度。注意,在两种环境中,元网络都在相应环境中接收目标信息g作为状态s的一部分。另外,实际上,可以将策略的分布参数直接包括在元损失输入中,例如 高斯策略的均值μ和标准差σ比包括概率估计πθ(a|s)更好,因为它提供了一种更直接的方法来使用通过元损失的反向传播进行更新。
4 与原始的Ant环境相反,我们从状态中消除了外力。
D. Experiments: Regression and Classification Details

