按照书上的定义:堆是一个完全二叉树,且二叉树中的任意一个非叶子结点值都大于(小于)左右孩子结点值。利用这个原理可确定堆中的根节点为最大(小)值。
堆排序的思想:堆采用顺序存放。当用数组建立一个堆后,将堆中的根节点与堆的最后一个元素互换位置,即将最大(小)值输出,然后把除了最后一个元素以外的数组再构建成堆,再把此时堆中根节点与堆的最后一个元素互换位置(是堆,不是数组)。再不断循环此步骤即可实现有序。
思路中提到两个步骤:把数组构建成堆,将堆中的根节点与堆的最后一个元素互换位置。用代码实现这两个步骤即可实现堆排序。
先给出堆的示例图:
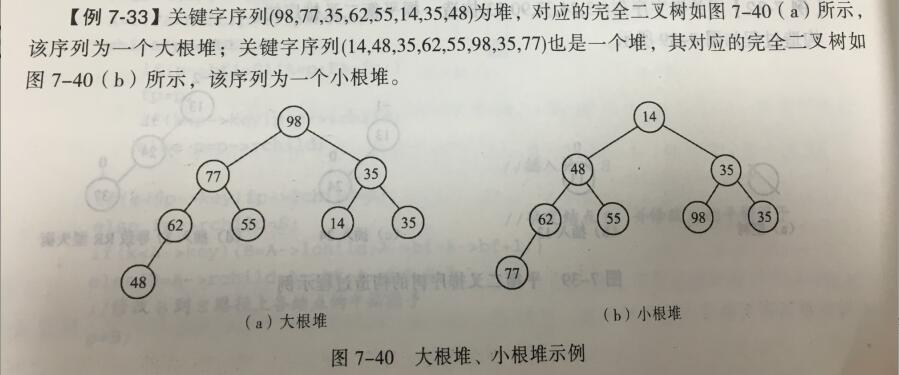
下图为构建堆的图解:
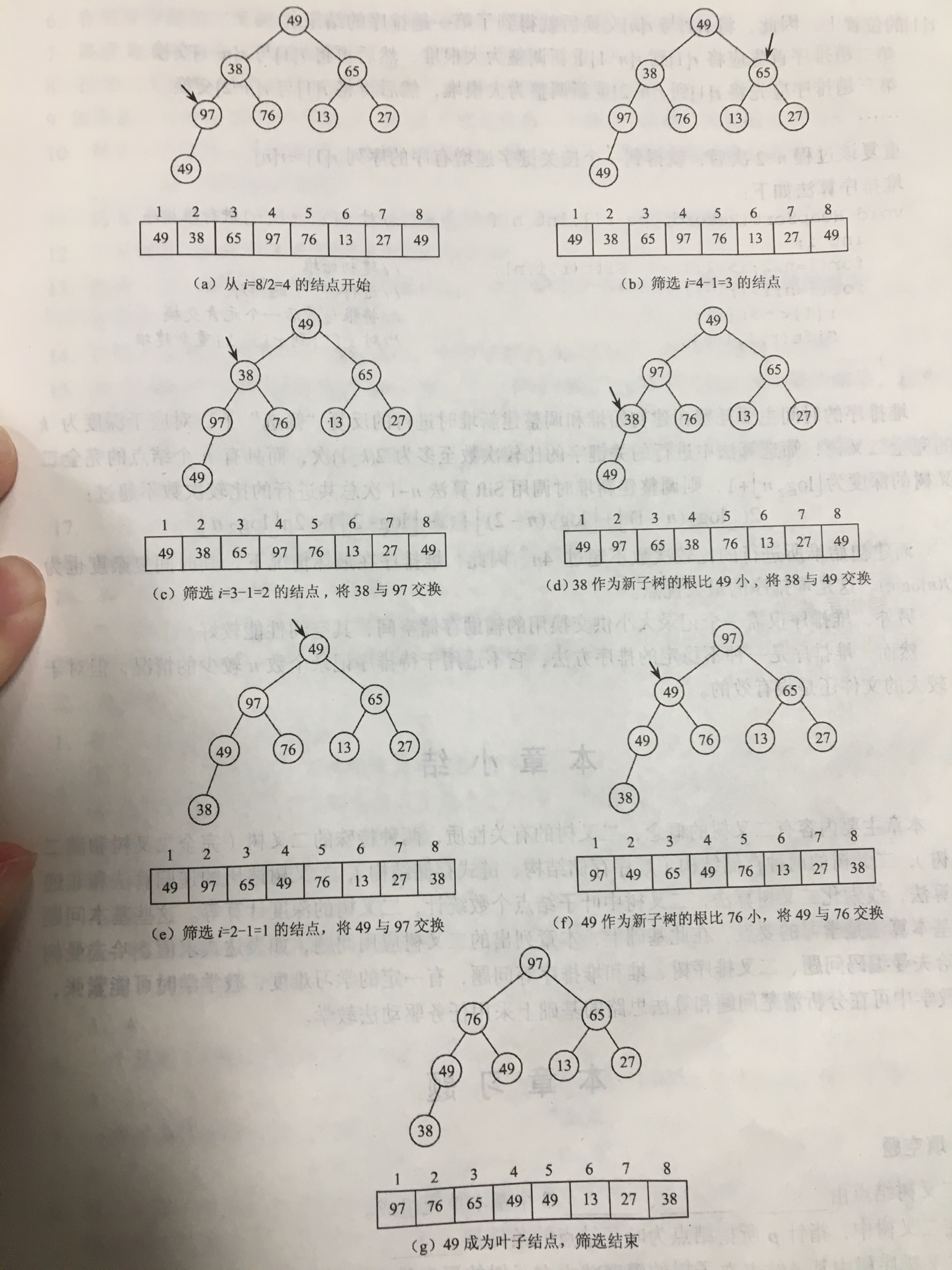
以上图为例,把97和38互换位置后,就要对除了97以外的数重新构建成堆。然后不断循环此步骤。
1 #include<stdio.h> 2 #define n 9 3 4 void heapSort(int num[]){ 5 6 int i,t; 7 for(i=n;i>0;i--){ 8 createHeap(num,i); 9 t = num[1]; //使根节点与堆中最后一个元素互换 10 num[1] = num[i]; 11 num[i] = t; 12 } 13 14 15 } 16 17 void createHeap(int num[],int m){ 18 19 int i; 20 for(i=m/2;i>0;i--) 21 sift(num,i,m); //利用堆的性质,让非叶子结点都大于或小于左右孩子结点 22 23 } 24 25 void sift(int num[],int k,int m){ 26 27 int i,j,t; 28 i = k; //非叶子结点 29 j = i * 2; //左孩子 30 31 while(j<=m){ //子结点必须在二叉树中 32 if(j<m && num[j]<num[j+1]) 33 j++; //选出左右孩子结点中较大的 34 35 if(num[i]<num[j]){ //如果父节点小于孩子结点 36 t = num[i]; //就是其互换 37 num[i] = num[j]; 38 num[j] = t; 39 i = j; //向下循环 40 j *= 2; //进入孩子结点的孩子结点 41 } 42 else //如果子节点不在二叉树内了,则直接退出循环 43 break; 44 } 45 46 } 47 48 void main(){ 49 50 int i,num[] = {-1,10,20,9,61,51,90,43,88,19}; //下标为0的位置没有使用 51 heapSort(num); 52 53 for(i=1;i<=n;i++) 54 printf("%d ",num[i]); 55 56 }