过拟合问题
上一章说了逻辑回归，这一章我们来看一下在机器学习中会碰到的一个十分常见的问题，过拟合问题是如何产生的以及我们怎样可以解决这个问题。
还是以前的老问题，假如我们需要通过房子的大小来拟合房子的价格。上面的三张图就是不同的假设函数之下拟合的结果。首先看最左边那张图，我们选择的是直线的假设函数，可以看得出来拟合的效果并不是太好，既没有让点很好地分布在上面也没有反映出数据的趋势，这就是欠拟合(underfitting)。于是我们加上一个二次项之后得到了中间那张图可以看得出来拟合效果还是不错的。我们再看看最右边的那张图片，我们添加到了四次项这条曲线让所有训练的点都分布在了上面，但是通过常识也能看出来这个图像反应的形状，如果这个时候我们给它一个新的size让它来预测基本上都会错。也就是说这个模型的泛化能力太差了，也就是出现了过拟合的问题(overfitting)。
接下来我们来分析一下为什么会导致这种问题的出现。从上面的问题可以很明显地看出来这个问题出现的根源就是特征数量过多而训练样本不足以约束住这么多特征变量。
那如何来解决这个问题？一般会有两种解决方式，第一种就是删除一些特征变量（可以通过人工删除，也可以通过一些学习算法来删除），第二种就是正则化。首先，我们来看一下第一种方式，其实我们很多情况下都会遇到每一个变量都与结果有关系，我们删除一些特征之后也就代表了我们的模型之中忽略了这些特征变量，其实这是不准确的。所以我们需要学习利用正则化来解决过拟合的问题。
正则化损失函数
这里，我们希望惩罚theta3和theta4来让其变得很小，从而让整个模型变得更接近二次函数。
于是在不改变假设函数的情况之下，我们很容易想到了改变损失函数。我们在损失函数的后面加上1000theta32和1000theta42,这样我们在优化损失函数的时候自然会将这两个参数变得很小。
线性回归的正则化
我们接下来看看正则化在线性回归中怎么使用。要想看如何使用也就是要看线性回归中的两个常用方法，梯度下降和正规方程。
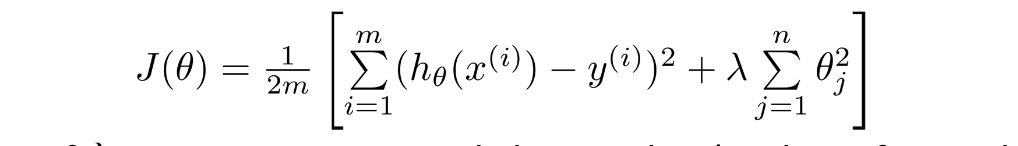这就是我们现在的线性回归损失函数，需要注意的是一般规定不对theta0进行惩罚。因此从1开始加。
梯度下降正则化
这就是正则化线性回归的梯度下降算法，这里和以前梯度算法都是一样的，求偏导数就行。
正规方程正则化
在这里插入图片描述这就是正规方程正则化的公式，矩阵左上角为0同样是不对theta0惩罚。当然，有人会问没有逆矩阵咋办，这里需要说的是加上这个部分之后一定存在逆矩阵。
逻辑回归正则化
梯度下降
这里和线性回归一样，我就不再赘述了。
其它的高级算法
我在我的github上面已经上传了这次正则化的python实现，有兴趣的可以看一下。
https://github.com/lsl1229840757/machine_learning/tree/master/programming_ex2