稀疏数组

概述

　　稀疏数组是指那些零元个数远大于非零元个数的数组，而稀疏数组的零元分布往往没有规律可循。最经典的例子就是棋盘，在保存棋局时，棋盘上棋子的数目往往不会布满整个棋盘。以中国象棋为例，棋盘为10*9，而棋子数为32，而且在走棋过程中还会减少棋子数。所以如果用整个数组来保存棋盘就会花费太多空间。这时就要对稀疏数组进行压缩存储。

　　压缩存储的处理方法是：

　　1. 创建一个小规模的二维数组，其列数为3，分别记录行、列、值。

　　2. 第一行记录原数组的行数、列数，以及非零元个数。

　　3. 之后每一行记录每一个非零元在原数组中的行位标、列位标和值。

　　以这个棋盘为例：

　　

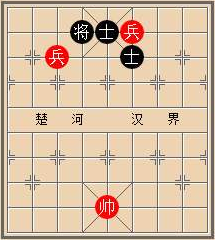
　　用两位数表示一个棋子：

　　1. 个位数：1表示兵、卒；2表示炮、砲；3表示车；4表示马；5表示相、象；6表示仕、士；7表示帅、将。

　　2. 十位数：1表示红方；2表示黑方。

　　比如，黑方用2表示，将用7表示，所以黑方的将用27表示；红方用1表示，兵用1表示，所以红方的兵用11表示。

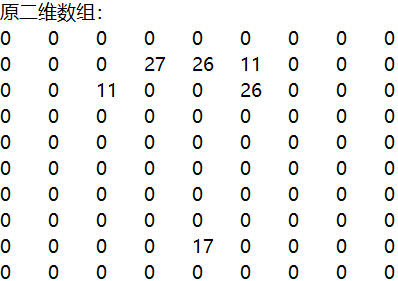
　　用一个10*9的二维数组存储棋盘，则这个棋盘可以表示为：

　　

　　即二维数组board中，board[1][3]=27，board[1][4]=26，board[1][5]=11，board[2][2]=11，board[2][5]=26，board[8][4]=17。

　　对该二维数组进行压缩：

　　1. 一共需要存储6个棋子，所以压缩后数组为sparseBoard[7][3]。

　　2. 第一行存储二维数组的行数、列数和棋子数，即sparseBoard[0]=10，sparseBoard[1]=9，sparseBoard[2]=6。

　　3. 之后6条记录分别存取棋子。

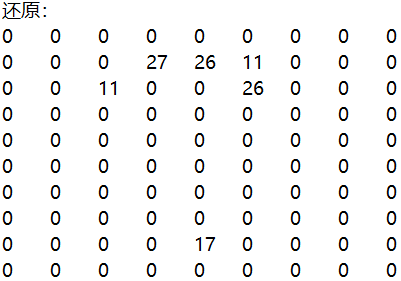
　　最终得到的结果为：

　　

代码实现

　　压缩稀疏数组：

public static int[][] compress(int[][] arr) {
    if (arr == null) return null;
    // 行数
    int m = arr.length;
    // 列数
    int n = arr[0].length;
    // 非零元个数
    int num = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (arr[i][j] != 0) {
                num++;
            }
        }
    }
    // 创建压缩后的数组，列数为3，行数为1+非零元个数
    int[][] cArr = new int[1 + num][3];
    // 第一行记录原数组的行数、列数，以及非零元个数
    cArr[0][0] = m;
    cArr[0][1] = n;
    cArr[0][2] = num;
    // 每一行记录每一个非零元在原数组中的行位标、列位标和值
    for (int i = 0, k = 1; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (arr[i][j] != 0) {
                cArr[k][0] = i;
                cArr[k][1] = j;
                cArr[k][2] = arr[i][j];
                k++;
            }
        }
    }
    return cArr;
}

　　将压缩后的数组还原为稀疏数组：

public static int[][] recovery(int[][] cArr) {
    if (cArr == null || cArr[0].length != 3) return null;
    // 第一行的前两个单元存储了原二维数组的行数和列数
    int[][] arr = new int[cArr[0][0]][cArr[0][1]];
    // 将除第一行外每一行还原到二维数组中，每一行的前两个单元为行位标和列位标，第三个单元为元素值
    for (int i = 1; i <= cArr[0][2]; i++) {
        arr[cArr[i][0]][cArr[i][1]] = cArr[i][2];
    }
    return arr;
}

　　测试：