前言:
大概两三周没动这块了,最近要抓紧时间复习并写博客记录,此次为利用sklearn库来解决非线性逻辑回归问题
正文:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
#make_gaussian_quantiles函数
#这个函数可以用来生成数据,不需要自己进行数据写入
from sklearn.datasets import make_gaussian_quantiles
from sklearn.preprocessing import PolynomialFeatures
#将生成2维正太分布,生成的而数据按分位数分为两类,500个样本,2个样本特征
#生成两类或多类数据
#n_samples是样本个数 n_features是样本特征 n_classes是样本类型
#将生成好的数据放入x_data和y_data里
x_data,y_data = make_gaussian_quantiles(n_samples = 500,n_features = 2,n_classes = 2)
#c代表颜色,即将y_data里的两类数据进行比较,是哪一类就用哪一种类型的颜色
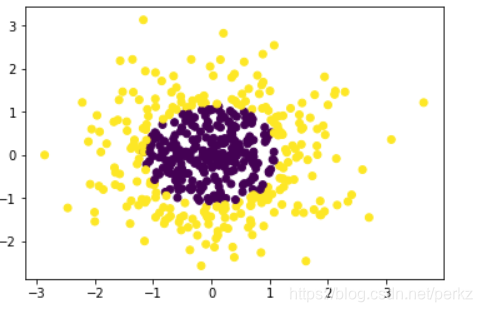
plt.scatter(x_data[:,0],x_data[:,1],c = y_data)
plt.show()
利用函数数据画出的图像如下:
logistic = linear_model.LogisticRegression()
#这里是利用源数据来进行处理,没有做任何改动
logistic.fit(x_data,y_data)
#获取数据值所在范围,方便画图并规定x,y轴的界限
x_min,x_max = x_data[:,0].min()-1,x_data[:,0].max()+1
y_min,y_max = x_data[:,1].min()-1,x_data[:,1].max()+1
#生成网格矩阵
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),
np.arange(y_min,y_max,0.02))
#ravel函数能将多维数据转化为一维数据,np.c_函数需要这种类型的数据
z = logistic.predict(np.c_[xx.ravel(),yy.ravel()])
z = z.reshape(xx.shape)
#等高线图
cs = plt.contourf(xx,yy,z)
#样本散点图
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
#利用logistic.score函数来计算这个模型的准确率
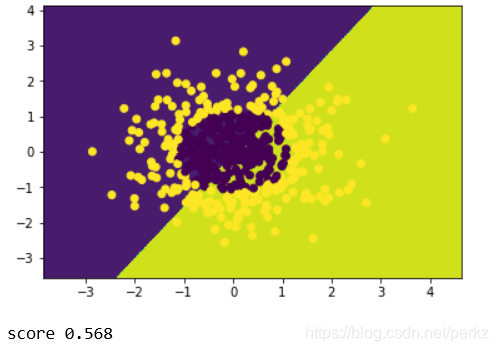
#结果为0.568,并不理想
print('score',logistic.score(x_data,y_data))
图片展示如下,可以看出正确率很低,还不如自己猜:
#由于并不理想,所以要继续进行处理
poly_reg = PolynomialFeatures(degree=5)
#特征处理
#这次才正在明白,经过处理后的数据会得到很多非线性逻辑的特征
#以前只是用,但不懂是什么意思
x_poly = poly_reg.fit_transform(x_data)
#定义逻辑回归模型
logistic = linear_model.LogisticRegression()
#训练模型
logistic.fit(x_poly,y_data)
#获取数据值所在的范围
x_min,x_max = x_data[:,0].min()-1,x_data[:,0].max()+1
y_min,y_max = x_data[:,1].min()-1,x_data[:,1].max()+1
#生成网格矩阵
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),
np.arange(y_min,y_max,0.02))
#将转型过的数据再进行处理
z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(),yy.ravel()]))
z = z.reshape(xx.shape)
#等高线图
cs = plt.contourf(xx,yy,z)
#样本散点图
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
plt.show()
print('score',logistic.score(x_poly,y_data))
经过处理的数据带入图像如下:
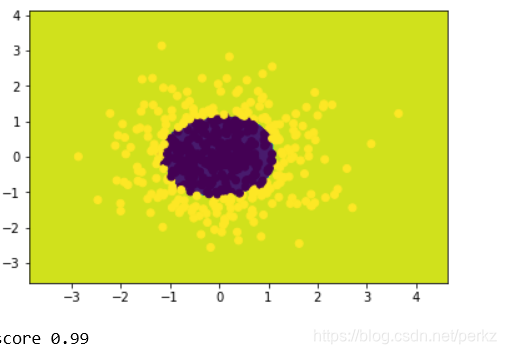
正确率达到了百分之99,可见提前处理数据是非常必要的。
总结:
利用sklearn库来解决非线性逻辑回归是很可取的方法,可以简单快捷的解决此类问题。