ceres---相机重投影误差

相机重投影误差

相机归一化公式：

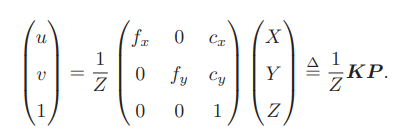
相机归一化与外参变换公式：

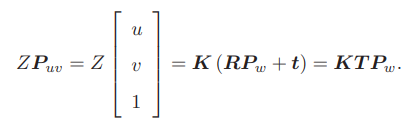
相机畸变：

 

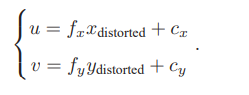
代码：

// Templated pinhole camera model for used with Ceres.  The camera is
// parameterized using 9 parameters: 3 for rotation, 3 for translation, 1 for
// focal length and 2 for radial distortion. The principal point is not modeled
// (i.e. it is assumed be located at the image center).
struct SnavelyReprojectionError {
  SnavelyReprojectionError(double observed_x, double observed_y)
      : observed_x(observed_x), observed_y(observed_y) {}

  template <typename T>
  bool operator()(const T* const camera,
                  const T* const point,
                  T* residuals) const {
    // camera[0,1,2] are the angle-axis rotation.
    T p[3];
    AngleAxisRotatePoint(camera, point, p);

    // camera[3,4,5] are the translation.
    p[0] += camera[3];
    p[1] += camera[4];
    p[2] += camera[5];

    // Compute the center of distortion. The sign change comes from
    // the camera model that Noah Snavely's Bundler assumes, whereby
    // the camera coordinate system has a negative z axis.
    const T xp = - p[0] / p[2];
    const T yp = - p[1] / p[2];

    // Apply second and fourth order radial distortion.
    const T& l1 = camera[7];
    const T& l2 = camera[8];
    const T r2 = xp*xp + yp*yp;
    const T distortion = 1.0 + r2  * (l1 + l2  * r2);


    // Compute final projected point position.
    const T& focal = camera[6];
    const T predicted_x = focal * distortion * xp;
    const T predicted_y = focal * distortion * yp;

    // The error is the difference between the predicted and observed position.
    residuals[0] = predicted_x - observed_x;
    residuals[1] = predicted_y - observed_y;

    return true;
  }

  // Factory to hide the construction of the CostFunction object from
  // the client code.
  static ceres::CostFunction* Create(const double observed_x,
                                     const double observed_y) {
    return (new ceres::AutoDiffCostFunction<SnavelyReprojectionError, 2, 9, 3>(
                new SnavelyReprojectionError(observed_x, observed_y)));
  }

  double observed_x;
  double observed_y;
};

// Templated pinhole camera model for used with Ceres.  The camera is
// parameterized using 10 parameters. 4 for rotation, 3 for
// translation, 1 for focal length and 2 for radial distortion. The
// principal point is not modeled (i.e. it is assumed be located at
// the image center).
struct SnavelyReprojectionErrorWithQuaternions {
  // (u, v): the position of the observation with respect to the image
  // center point.
  SnavelyReprojectionErrorWithQuaternions(double observed_x, double observed_y)
      : observed_x(observed_x), observed_y(observed_y) {}

  template <typename T>
  bool operator()(const T* const camera,
                  const T* const point,
                  T* residuals) const {
    // camera[0,1,2,3] is are the rotation of the camera as a quaternion.
    //
    // We use QuaternionRotatePoint as it does not assume that the
    // quaternion is normalized, since one of the ways to run the
    // bundle adjuster is to let Ceres optimize all 4 quaternion
    // parameters without a local parameterization.
    T p[3];
    QuaternionRotatePoint(camera, point, p);

    p[0] += camera[4];
    p[1] += camera[5];
    p[2] += camera[6];

    // Compute the center of distortion. The sign change comes from
    // the camera model that Noah Snavely's Bundler assumes, whereby
    // the camera coordinate system has a negative z axis.
    const T xp = - p[0] / p[2];   //  x/z
    const T yp = - p[1] / p[2];    // y/z

    // Apply second and fourth order radial distortion.
    const T& l1 = camera[8];
    const T& l2 = camera[9];

    const T r2 = xp*xp + yp*yp;
    const T distortion = 1.0 + r2  * (l1 + l2  * r2);

    // Compute final projected point position.
    const T& focal = camera[7];
    const T predicted_x = focal * distortion * xp;
    const T predicted_y = focal * distortion * yp;

    // The error is the difference between the predicted and observed position.
    residuals[0] = predicted_x - observed_x;
    residuals[1] = predicted_y - observed_y;

    return true;
  }

  // Factory to hide the construction of the CostFunction object from
  // the client code.
  static ceres::CostFunction* Create(const double observed_x,
                                     const double observed_y) {
    return (new ceres::AutoDiffCostFunction<
            SnavelyReprojectionErrorWithQuaternions, 2, 10, 3>(
                new SnavelyReprojectionErrorWithQuaternions(observed_x,
                                                            observed_y)));
  }

  double observed_x;
  double observed_y;
};