The gray code is a binary numeral system where two successive values differ in only one bit.
Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.
For example, given n = 2, return[0,1,3,2]. Its gray code sequence is:
00 - 0 01 - 1 11 - 3 10 - 2
Note:
For a given n, a gray code sequence is not uniquely defined.
For example,[0,2,3,1]is also a valid gray code sequence according to the above definition.
For now, the judge is able to judge based on one instance of gray code sequence. Sorry about that.
题意:给定n表示格雷码的位数,打印格雷码序列。
思路:首先要明白什么是格雷码。在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码(Gray Code),另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。如当n=2时,每个数之间的格雷码只有一位不同。
方法一:利用二进制转格雷码的转化公式:(num>>1)^num,注:num是非负整数,>>是右移操作,^是异或。先将二进制数的个数转换成范围,然后利用公式即可。代码如下:
1 class Solution { 2 public: 3 vector<int> grayCode(int n) 4 { 5 vector<int> res; 6 for(int i=0;i<pow(2,n);++i) //pow函数为以2为底的n次方 7 { 8 res.push_back((i>>1)^i); 9 } 10 return res; 11 } 12 };
其中第6行pow()函数可以变成先定义一个变量,然后用这个值带入
1 int num=1<<n;
方法二:来自Grandyang的博客。 n元格雷码可以从n-1位元的格雷码以上下镜像后加上新位元的方式快速得到
代码如下:
1 class Solution 2 { 3 public: 4 vector<int> grayCode(int n) 5 { 6 vector<int> res{0}; 7 for(int i=0;i<n;++i) 8 { 9 int size=res.size(); 10 for(int j=size-1;j>=0;--j) 11 { 12 res.push_back(res[j]|(1<<i)); 13 } 14 } 15 return res; 16 } 17 };
1)格雷码 转 二进制码(摘自百度百科):
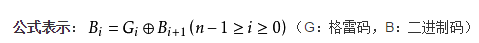
2)
-
对n位二进制的码字,从右到左,以0到n-1编号
-
如果二进制码字的第i位和i+1位相同,则对应的格雷码的第i位为0,否则为1(当i+1=n时,二进制码字的第n位被认为是0,即第n-1位不变)公式表示:
注意:格雷码转二进制码和二进制码转格雷的区别:前者是异或后的值再和下一位异或,后者是直接两相邻元素异或。