求解斐波那契数列的第n项

　　对于Fibonacci数列，1,1,2,3,5,8,12,...求解第n项值，我们通常用的是递归算法，即递推式f(n) = f(n-1)+f(n-2).然而这其实是一种效率极低的算法，当n达到41时，就已经需要1s左右，随着n的增加，时间是指数级增长的。

　　因为该递归算法有太多的重复计算,如下图所示，所用时间T(n) = T(n-1)+T(n-2)+Θ(1)，可以知道T(n)有Ω((3/2)ⁿ)的下界,T(n)<O(2^n),可以看到这是指数级的时间复杂度。

　　　　　　　　　　　　　

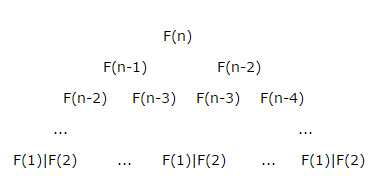
　　具体代码实现如下：

Elemtype Fibonacci(int n)
{
    if(n==1||n==2)
        return 1;
    else
        return Fibonacci(n-1)+Fibonacci(n-2);
}

　　基于这种情况，我们首先想到的就是使用迭代法改写，代码如下所示：

Elemtype Fibonacci_Iterate(int n)
{
    if(n==1||n==2) return 1;
    Elemtype f1 = 1,f2 = 1;
    for(int j=3;j<=n;++j){
        Elemtype temp = f1+f2;
        f1 = f2;
        f2 = temp;
    }
    return f2;
}

　　迭代法具有O(n)的时间复杂度。

　　其实斐波那契数列还有一种O(logⁿ)的算法，那就是用矩阵乘法，如下图所示，该公式可以由归纳法证明。用这个公式求F(n)则可以用分治法，求矩阵的n次方我们只需求n/2次方，然后对其结果再进行一次矩阵乘法。如果n的是奇数，我们就先对n-1做该计算，在将其结果与矩阵matrix进行一次矩阵乘法。假设求F(n)需要时间T(n),T(n) = T(n/2)+Θ(1),所以其时间复杂度为O(logⁿ).

　　　　　　　　　　　　　　　　　　

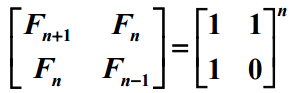
　　C语言代码实现如下，每当递归返回时，free掉下一层申请的内存。

Elemtype matrix[4] = {1,1,1,0};
                    
Elemtype* MultipMatrix(Elemtype *m1,Elemtype *m2)
{    
    Elemtype *ret = (Elemtype*)malloc(sizeof(Elemtype)*4);
    ret[0] = m1[0]*m2[0]+m1[1]*m2[2];
    ret[1] = m1[0]*m2[1]+m1[1]*m2[3];
    ret[2] = m1[2]*m2[0]+m1[3]*m2[2];
    ret[3] = m1[2]*m2[1]+m1[3]*m2[3];
    return ret;
}    
                
Elemtype* Fibonacci_Matrix(int n)
{
    if(n==1) return matrix;
    Elemtype *temp = Fibonacci_Matrix(n >> 1);
    Elemtype *ret = NULL;
    if(n & 0x1){
        ret = MultipMatrix(MultipMatrix(temp,temp),matrix);
//        return MultipMatrix(MultipMatrix(temp,temp),matrix);
    }
    else{
        ret = MultipMatrix(temp,temp);
//        return MultipMatrix(temp,temp);        
    }
    if(temp!=matrix)
        free(temp);
    return ret;
}
//matrix method

　　对于迭代法和矩阵法，当n的规模越大，优势就越明显，当我用如下测试代码，所用时间约为0.17s，而改用迭代法实现的代码，用时达到了4s以上。

　　int n = 1000000;
    start = clock();
    for(int i=0;i<1000;++i){
        Elemtype *temp = Fibonacci_Matrix(n);
        printf("%lld
",temp[1]);
//        printf("%lld
",Fibonacci(n));
//        printf("%lld
",Fibonacci_Iterate(n));
    }
    end = clock();
    
    double t = ((double)(end-start))/CLK_TCK;
    printf("%f",t);

　　总结，如果我们的n的规模不是很大，则可以用迭代法，因为这种算法实现相对容易。当n规模很大时，则最好使用矩阵法，当然，此时的F(n)早已超出了C语言long long的范围，需要想办法另外实现更大整数的表示。

　　C语言的动态内存申请和释放使代码容易出错，所以可以考虑使用C++的智能指针来代替，或者定义一个矩阵类，实现=,*等矩阵运算。