洛谷P5463 小鱼比可爱（加强版） 题解

写博客不易，来玩会？

这道题我和dalao们的做法略有不同，我用的是归并排序做法qwq

归并排序求逆序对大家应该很清楚了，我这里就来讲讲如何用归并排序求出这道题的答案

让我们先观察一下规律

举个栗子，若存在一组逆序对a[3],a[4]，n = 5，则这组逆序对存在于以下区间内：[ 1 , 4 ] , [ 1 , 5 ] , [ 2 , 4 ] , [ 2 , 5 ] , [ 3 , 4 ] , [ 3 , 5 ]，共6个。我们可以画个图帮助理解：

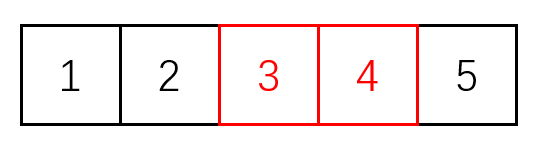
将其推广，若有逆序对a[ l ] , a[ r ]，如图所示：

则包含其的区间数，即该区间对答案的贡献为(l + 1 - 1) * (n - r + 1 ) = l * (n-r+1)。

然后再用归并排序即可。

注意两个点：

1.本题要用一个类似前缀和的变量来记录所有左半边的位置之和，搜到的时候再从(sum)中减去，否则会T（至少我T了）

2.会爆精度。记得开__int 128或者打高精（反正我开的__int 128 qwq）

code：

// Author : Kasugano_Sora
#include<bits/stdc++.h>
using namespace std;
struct item
{
    int pl , val;
} a[1100000] , b[1100000];
int n;
__int128 ans;
inline __int128 read()
{
    __int128 x = 0 , f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

inline void print( __int128 x )    //int 128必备操作
{
    if(x < 0)
    {
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
void msort( int l , int r )
{
    if(l == r)
    return ;
    int mid = (l + r) >> 1;
    msort(l , mid);
    msort(mid + 1 , r);
    long long sum = 0LL;        //所谓的前缀
    for(int i = l ; i <= mid ; i++ )
    {
        sum += 1ll * a[i].pl;
    }
    int i = l , j = mid + 1 , k = l;
    while(1)        //归并
    {
        if(i > mid || j > r)
        break;
        if(a[i].val <= a[j].val)
        sum -= 1ll * a[i].pl , b[k++] = a[i++];
        else
        {
            ans += sum * 1ll * (n - a[j].pl + 1);
            b[k++] = a[j++];
        }
    }
    if(i > mid) for( ; j <= r ; j++ , k++ )
    {
        b[k] = a[j];
    }
    else for( ; i <= mid ; i++ , k++ )
    {
        b[k] = a[i];
    }
    for(int i = l ; i <= r ; i++ )
    {
        a[i] = b[i];
    }
    return ;
}
int main()
{
//	freopen("1.txt" , "r" , stdin);
    cin >> n;
    for(int i = 1 ; i <= n ; i++ )
    {
    	scanf("%d" , &a[i].val);
    	a[i].pl = i;
    }
    msort(1 , n);
    print(ans);
    return 0;
}