numpy简介
numpy 是真正意义上的数组,一个二维矩阵的每一行都可以看做是一条记录。numpy主要是用来帮我们做数值矩阵操作的
属性
import numpy as np
vector = np.array([1,2])
vector
Out[4]: array([1, 2])
metrix = np.array([[1,2], [3,4]])
metrix
Out[6]:
array([[1, 2],
[3, 4]])
metrix.ndim
Out[8]: 2
metrix.size
Out[9]: 4
metrix.shape
Out[10]: (2, 2)
vector.shape
Out[11]: (2,)
一维向量的(2,) 其中的2不表示有2行,而是表示有2个数据
numpy的创建
In [32]: np.array([1,2,3])
Out[32]: array([1, 2, 3])
In [33]: np.array(range(12))
Out[33]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
In [34]: np.arange(12)
Out[34]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
dtype指定数组类型
vector = np.array([1,3,5], dtype=np.float)
print(vector)
[1. 3. 5.]
不用array方法
np.zeros((3,4), dtype=np.int16)
Out[21]:
array([[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]], dtype=int16)
np.ones((3,4))
Out[22]:
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
np.arange(12)
Out[23]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
np.arange(4,12,2)
Out[24]: array([ 4, 6, 8, 10])
np.linspace(1,10,3)
Out[25]: array([ 1. , 5.5, 10. ])
linspace(1,10,3) 表示1到10总共分为3段
修改数据类型
n1 = n1.astype(np.float)
数组形状的改变
一维到二维
In [40]: n2 = np.arange(12)
In [41]: n2.reshape((3,4))
Out[41]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
二维到一维
In [42]: n2.reshape((3,4)).flatten()
Out[42]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
无论维度怎么转换,都是在array类型中转来转去
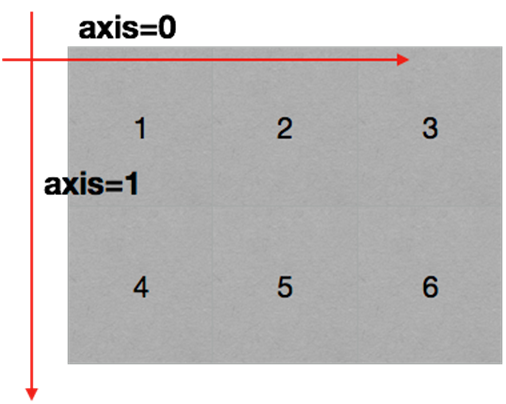
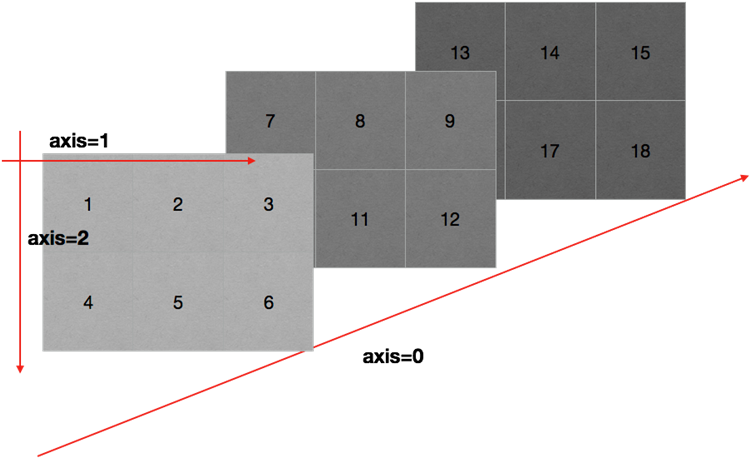
数组的维度
在numpy中可以理解为方向,使用0,1,2...数字表示,对于一个一维数组,只有一个0轴,对于2维数组(shape(2,2)),有0轴和1轴,对于三维数组(shape(2,2, 3)),有0,1,2轴
回顾np.arange(0,10).reshape((2,5)),reshpe中2表示0轴长度(包含数据的条数)为2,1轴长度为5,2X5一共10个数据
numpy读取数据
numpy读取数据我们一般是用不到的,读数据一般是采用pandas进行读取
np.loadtxt(fname,dtype=np.float,delimiter=None,skiprows=0,usecols=None,unpack=False)

fname 是文件路径, dtype 指定读取数据做的类型转换
例如有如下的数据格式文件
4394029,320053,5931,46245
7860119,185853,26679,0
5845909,576597,39774,170708
2642103,24975,4542,12829
1168130,96666,568,6666
1311445,34507,544,3040
666169,9985,297,1071
读取应该这样操作
t2 = np.loadtxt(file_path,delimiter=",",dtype="int")
unpack=True 表示读取的数据之后进行转置,一般不用这个参数
numpy的基础运算
矩阵和当个值进行运算其实就是和所有值进行运算,俗称广播原则
a = np.array([1,3,4])
a + 2
Out[4]: array([3, 5, 6])
a ** 2
Out[5]: array([ 1, 9, 16], dtype=int32)
a == 3
Out[6]: array([False, True, False])
b = (a == 3)
b
Out[8]: array([False, True, False])
a[b]
Out[9]: array([3])
矩阵的乘法
a = np.arange(2,6).reshape((2,2))
a
Out[17]:
array([[2, 3],
[4, 5]])
b = np.arange(4,8).reshape((2,2))
a * b
Out[19]:
array([[ 8, 15],
[24, 35]])
a.dot(b)
Out[20]:
array([[26, 31],
[46, 55]])
a
Out[25]:
array([[2, 3],
[4, 5]])
a.T
Out[26]:
array([[2, 4],
[3, 5]])
矩阵的最大,最小和中位数
a = np.random.random((2,3))
a.max()
Out[31]: 0.643734095861461
a.min()
Out[32]: 0.13837909149435934
a.mean()
Out[33]: 0.3217103031644281
a = np.arange(1,5)
a
Out[37]: array([1, 2, 3, 4])
a.reshape((2,2))
Out[38]:
array([[1, 2],
[3, 4]])
a
Out[39]: array([1, 2, 3, 4])
reshape并不会更改原来的矩阵
a = np.arange(1,5).reshape(2,2)
a
Out[41]:
array([[1, 2],
[3, 4]])
a.sum(axis=0)
Out[42]: array([4, 6])
axis=0表示对数列进行求和运算,在这里我们无需关注计算显示的格式,我们的出发点应该是计算得到的结果都是矩阵
a = np.arange(3,7).reshape((2,2))
a
Out[46]:
array([[3, 4],
[5, 6]])
a.argmax()
Out[47]: 3
a.cumsum()
Out[48]: array([ 3, 7, 12, 18], dtype=int32)
np.diff(a)
Out[49]:
array([[1],
[1]])
a = np.arange(2, 14).reshape((3,4))
a
Out[51]:
array([[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]])
a.nonzero()
Out[52]:
(array([0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2], dtype=int64),
array([0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3], dtype=int64))
排序
a = np.array([[1,3,2,7],[4,5,10,3]])
a
Out[71]:
array([[ 1, 3, 2, 7],
[ 4, 5, 10, 3]])
a.sort()
a
Out[73]:
array([[ 1, 2, 3, 7],
[ 3, 4, 5, 10]])
a = np.array([[8,2,3], [1,5,4]])
a
Out[77]:
array([[8, 2, 3],
[1, 5, 4]])
a.sort(axis=0)
a
Out[79]:
array([[1, 2, 3],
[8, 5, 4]])
索引和切片
通用格式 a[ , ], 其中, 前面的是行,,后面的是列
取一行
In [50]: n1
Out[50]:
array([[ nan, 1., 2., 3.],
[ 4., 4., 6., 7.],
[ 8., 4., 10., 11.]])
In [51]: n1[0,:]
Out[51]: array([ nan, 1., 2., 3.])
可以简写为
In [52]: n1[0]
Out[52]: array([ nan, 1., 2., 3.])
取连续的多行
In [57]: n1[0:2]
Out[57]:
array([[ nan, 1., 2., 3.],
[ 4., 4., 6., 7.]])
取不连续的多行
In [59]: n1
Out[59]:
array([[ nan, 1., 2., 3.],
[ 4., 4., 6., 7.],
[ 8., 4., 10., 11.]])
In [60]: n1[[0,2]]
Out[60]:
array([[ nan, 1., 2., 3.],
[ 8., 4., 10., 11.]])
取一个元素
In [61]: n1[2,3]
Out[61]: 11.0
取多个元素
取出的元素坐标是(0,1) 和 (2,2)
In [62]: n1[[0,2],[1,2]]
Out[62]: array([ 1., 10.])
想要得到数列,可以借助转置来实现
for column in a.T:
print(column)
a
Out[91]:
array([[1, 2, 3],
[8, 5, 4]])
a.flatten()
Out[92]: array([1, 2, 3, 8, 5, 4])
numpy的合并
a = np.array([1,1,1])
b = np.array([2,2,2])
np.vstack((a,b))
Out[95]:
array([[1, 1, 1],
[2, 2, 2]])
np.hstack((a,b))
Out[96]: array([1, 1, 1, 2, 2, 2])
a = np.array([1,1,1])
a[:,np.newaxis]
Out[4]:
array([[1],
[1],
[1]])
numpy的分割
np.split(a,2,axis=1)
Out[25]:
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2, 3],
[ 6, 7],
[10, 11]])]
a
Out[26]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
np.split(a,2,axis=1)
Out[27]:
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2, 3],
[ 6, 7],
[10, 11]])]
np.array_split(a,3)
Out[28]: [array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
np.array_split(a,3, axis=1)
Out[29]:
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2],
[ 6],
[10]]), array([[ 3],
[ 7],
[11]])]
numpy 数值的修改
直接赋值成一个变量或者列表或数组
In [7]: n1
Out[7]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [8]: n1[0] = 2
In [9]: n1
Out[9]:
array([[ 2, 2, 2, 2],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [10]: n1[0]=[1,2,3,3]
In [11]: n1
Out[11]:
array([[ 1, 2, 3, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
三元运算
把小于3的赋值成1, 大于3的赋值成12, 这样得到的值不是1就是12
In [13]: np.where(n1<3,1,12)
Out[13]:
array([[ 1, 1, 12, 12],
[12, 12, 12, 12],
[12, 12, 12, 12]])
裁剪
小于3的替换成3, 大于10的替换成10,这样得到的值不仅包含3和10,还会包含其他值
In [14]: n1
Out[14]:
array([[ 1, 2, 3, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [15]: n1.clip(3,10)
Out[15]:
array([[ 3, 3, 3, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 10]])
numpy 布尔索引
布尔型索引是我在接触numpy的时候给了我很大兴奋感的一个功能,布尔索引实现的是通过列向量中的每个元素的布尔量数值对一个与列向量有着同样行数的矩阵进行符合匹配。而这样的作用,其实是把列向量中布尔量为True的相应行向量给抽取了出来。
如果进行变量或者标定量的大数据处理,这种筛选功能的使用肯定会给程序的设计带来极大的便捷。在numpy中使用bool索引有两种方式
最自然的方式是布尔值数组与原数组有相同的形状
这个性质很适合用来给元素重新赋值
In [25]: data
Out[25]:
array([[ 0.77193091, 1.04445225, -0.21386348, -0.24080208, 1.64144532],
[ 2.13219977, -1.47110822, -0.10990423, 0.35145366, -0.79434474],
[-0.99331306, -0.87026845, -0.79164964, 0.58548195, 0.73012706],
[-0.73547341, 1.80731535, 0.63650607, 1.47816195, 1.29292191],
[ 0.28903558, 0.81603312, -1.19116416, 1.09452553, 0.75497327],
[-0.58125007, 0.61782017, 0.7624887 , -0.58346218, 0.6606624 ],
[-1.03606189, 0.24883092, 1.90600985, 0.135974 , 1.36715279]])
In [26]: data>0
Out[26]:
array([[ True, True, False, False, True],
[ True, False, False, True, False],
[False, False, False, True, True],
[False, True, True, True, True],
[ True, True, False, True, True],
[False, True, True, False, True],
[False, True, True, True, True]], dtype=bool)
In [27]: data[data>0]
Out[27]:
array([ 0.77193091, 1.04445225, 1.64144532, 2.13219977, 0.35145366,
0.58548195, 0.73012706, 1.80731535, 0.63650607, 1.47816195,
1.29292191, 0.28903558, 0.81603312, 1.09452553, 0.75497327,
0.61782017, 0.7624887 , 0.6606624 , 0.24883092, 1.90600985,
0.135974 , 1.36715279])
In [28]: data[data>0] = 1
In [29]: data
Out[29]:
array([[ 1. , 1. , -0.21386348, -0.24080208, 1. ],
[ 1. , -1.47110822, -0.10990423, 1. , -0.79434474],
[-0.99331306, -0.87026845, -0.79164964, 1. , 1. ],
[-0.73547341, 1. , 1. , 1. , 1. ],
[ 1. , 1. , -1.19116416, 1. , 1. ],
[-0.58125007, 1. , 1. , -0.58346218, 1. ],
[-1.03606189, 1. , 1. , 1. , 1. ]])
data > 0 这种计算也会采用广播机制
第二种方式比较类似于整数索引;对数组每一维,我们提供一维的布尔数组来选择我们想要的值
>>> a = np.arange(12).reshape(3,4)
>>> b1 = np.array([False,True,True]) # first dim selection
>>> b2 = np.array([True,False,True,False]) # second dim selection
>>>
>>> a[b1,:] # 选择第2、3行的所有列
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> a[b1] # same thing
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
>>> a[:,b2] # selecting columns
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
>>>
>>> a[b1,b2] # 奇怪的事发生了
array([ 4, 10])
一维布尔数组的长度必须和你要切片的维(或axis)的长度相同。在上面的例子中,b1是长度为3的一维数组,b2是长度为4,适合索引数组a的第二维。
numpy中的NAN
numpy中的nan!=nan, 判断是否是nan有内置方法np.isna(), 但是却没有相反的方法
把numpy中的numpy替换成指定值
def fill_ndarray(t1):
for i in range(t1.shape[1]): #遍历每一列
temp_col = t1[:,i] #当前的一列
nan_num = np.count_nonzero(temp_col!=temp_col)
if nan_num !=0: #不为0,说明当前这一列中有nan
temp_not_nan_col = temp_col[temp_col==temp_col] #当前一列不为nan的array
# 选中当前为nan的位置,把值赋值为不为nan的均值
temp_col[np.isnan(temp_col)] = temp_not_nan_col.mean()
return t1
if __name__ == '__main__':
t1 = np.arange(24).reshape((4, 6)).astype("float")
t1[1, 2:] = np.nan
print(t1)
t1 = fill_ndarray(t1)
print(t1)
数组的行列交换
In [41]: n1
Out[41]:
array([[ 1, 2, 3, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
In [42]: n1[[0,2]] = n1[[2,0]]
In [43]: n1
Out[43]:
array([[ 8, 9, 10, 11],
[ 4, 5, 6, 7],
[ 1, 2, 3, 3]])
numpy 的统计方法
求和:t.sum(axis=None)
均值:t.mean(a,axis=None) 受离群点的影响较大
中值:np.median(t,axis=None)
最大值:t.max(axis=None)
最小值:t.min(axis=None)
极值:t.ptp(axis=None) 即最大值和最小值只差
标准差:t.std(axis=None)
需要额外注意是中值,这个方法只在numpy模块中才有
numpy 生成随机数

seed的用法, 有了seed,每次产生的值都会第一次随机产生的值一致
In [44]: np.random.rand(2)
Out[44]: array([ 0.76556093, 0.77899664])
In [45]: np.random.seed(4)
In [46]: np.random.rand(2)
Out[46]: array([ 0.96702984, 0.54723225])
In [47]: np.random.rand(2)
Out[47]: array([ 0.97268436, 0.71481599])
In [48]: np.random.rand(2)
Out[48]: array([ 0.69772882, 0.2160895 ])