三个圆围成的面积。
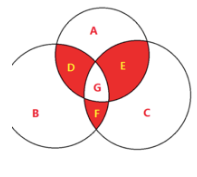
A + B + C - D - E - F + G


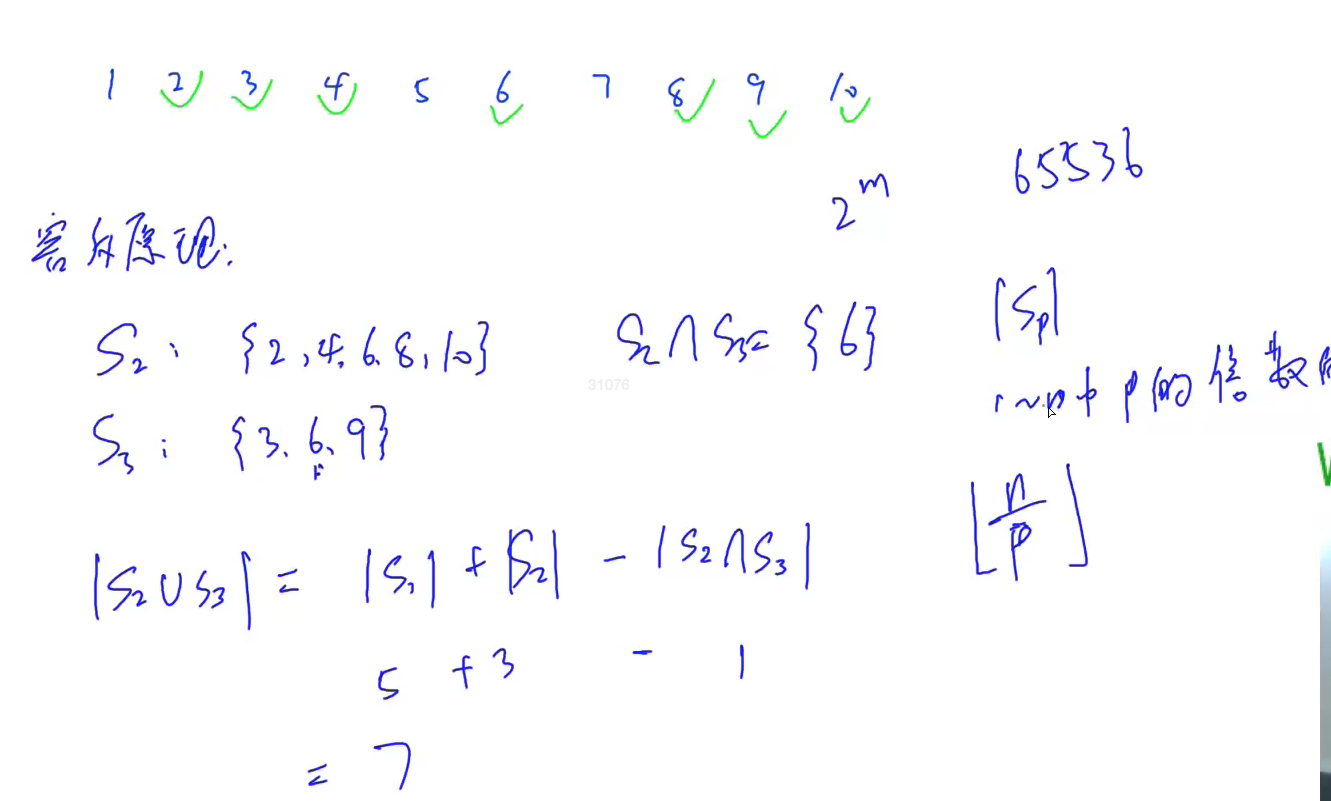
给定一个整数n和m个不同的质数p1,p2,…,pm。
请你求出1~n中能被p1,p2,…,pm中的至少一个数整除的整数有多少个。
输入格式
第一行包含整数n和m。
第二行包含m个质数。
输出格式
输出一个整数,表示满足条件的整数的个数。
输入样例:
10 2
2 3
输出样例:
7#include <iostream> #include <algorithm> using namespace std; typedef long long LL; const int N = 20; int p[N]; int main() { int n, m; cin>>n>>m; for(int i = 0;i<m;i++) cin>>p[i]; int res = 0; for(int i = 1; i < 1 << m; i++) { int t = 1, cnt = 0; //t表示所有质数的乘积,cnt是i里面包含几个1 for(int j = 0; j < m; j++) if(i >> j & 1) { cnt++; if((LL)t * p[j] > n) { t = -1; break; } t *= p[j]; } if(t != -1) { if(cnt % 2) res += n / t; else res -= n / t; } } cout<<res<<endl; }
m个质数能不能够被整除,可以用m位的二进制,往右移动从0到m位然后&1的结果,如果是1的话,那么这个质数可以被整除,然后cnt就代表容斥原理中被存在于几个集合当中,所有质数在或者不在的总数是2^m的,然后容斥原理的总数也是2^m:从选一个,两个……一直到m个。t存的就是i里包含几个1,即有几个奇数,奇数位就加上,偶数位就减。n能被p整除的个数是:floor(n / p)向下取取整的,直接就是 n / t 就是了。
这个题目求得是1~N里面能被m个质数p整除的个数,但是在这里我们没有运用到n能不能整除的东西,如果小于的话,那么直接用 n / t 来表示有几个,每个质数p有没有被除,就放在m位的二进制里面。