一、定义
在训练数据集上的准确率很⾼,但是在测试集上的准确率⽐较低
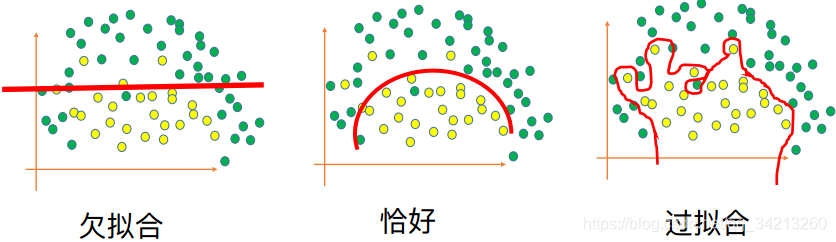
二、过拟合的解决方案
2.1 DropOut
假设有一个过拟合的神经网络如下:
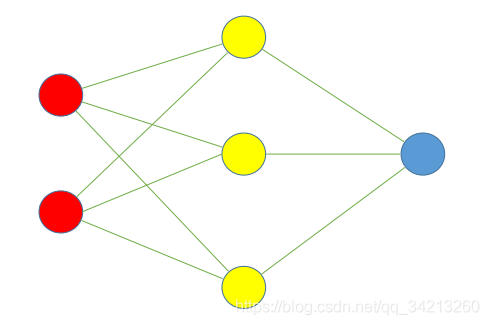
DropOut步骤:
- 根据DropOut rate(这里假设为 1/3),在每组数据训练时,随机选择每一隐藏层的1/3的节点去除,并训练。如下图是三次训练的过程:
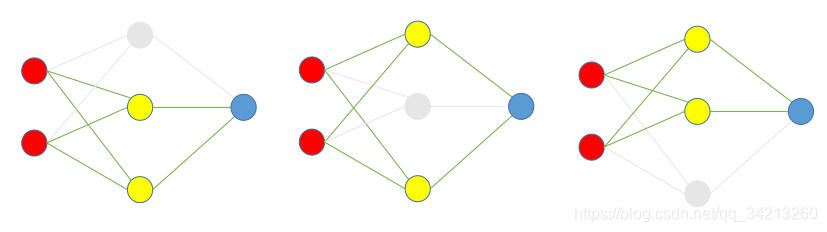 2. 使用时,把神经网络还原成原来没有去除过节点的样子,如下图。但是系数(w,b)需要乘以(1-DropOut rate)
2. 使用时,把神经网络还原成原来没有去除过节点的样子,如下图。但是系数(w,b)需要乘以(1-DropOut rate)

2.2 L2 正则化
2.2.1 方法
对损失函数(loss function) f(θ) 中的每一个系数θi,都对损失函数加上1/2λθi2,其中λ是正则化的强度。
- 相当于,在训练的每一次更新系数的时候都额外加上这一步:
θi= θi - λθi
2.2.2 目的
L2正则化的目的是使系数的绝对值减小,对绝对值越大的系数,减小的程度越强。L2正则化使得大多数系数的值都不为零,但是绝对值都比较小。
2.3 L1 正则化
2.3.1 方法
对损失函数(lossfunction)f(θ)中的每一个系数θi,都对损失函数
加上λ|θi|,其中λ是正则化的强度。
- 相当于,在训练的每一次更新系数的时候都额外加上这一步:
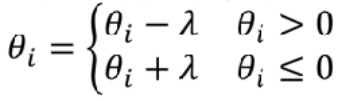
2.3.2 目的
L1正则化的目的是使得许多系数的绝对值接近0,其它那些系数不接近于0的系数对应的特征就是对输出有影响的特征。所以L1正则化甚至可以用于作为特征选择的工具。
2.4 最⼤范数约束 (Max Norm)
2.4.1 方法
对每一个神经元对应的系数向量,设置一个最大第二范数值c,这个值通常设为3。如果一个神经元的第二范数值大于c,那么就将每一个系数值按比例缩小,使得第二范式值等于c。
-
相当于在训练的每一次更新系数的时候都额外加上这一步:
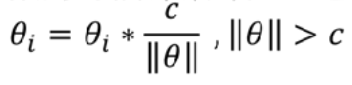
注意:只有当||θ||>c才执行
2.4.2 目的
由于最大范数的约束,可以防止由于训练步长较大引发的过拟合。