目录:




什么是齐次坐标?
简单的说:齐次坐标就是在原有坐标上加上一个维度:
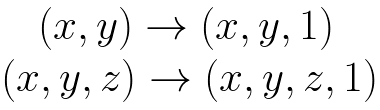
使用齐次坐标有什么优势?
1、能非常方便的表达点在直线或平面上
在2D平面上,一条直线 l 可以用方程 ax + by + c = 0 来表示,该直线用向量表示的话一般记做

我们知道点p = (x, y)在直线 l 上的充分必要条件是 ax + by + c = 0
如果使用齐次坐标的话,点p的齐次坐标就是
p'=(x, y, 1)
那么 ax + by + c = 0 就可以用两个向量的内积(点乘)来表示:
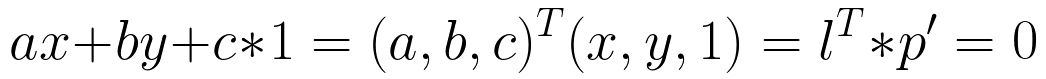
因此,点p在直线l上的充分必要条件就是 直线l 与p的齐次坐标p'的内积:

是不是很方便呢!
同理,我们知道 三维空间的一个平面A可以用方程 ax + by + cz + d = 0 来表示,三维空间的一个点P=(x, y, z) 的齐次坐标 P'=(x, y, z, 1),类似的,点P在空间平面A上可以用两个向量的内积来表示,如下:
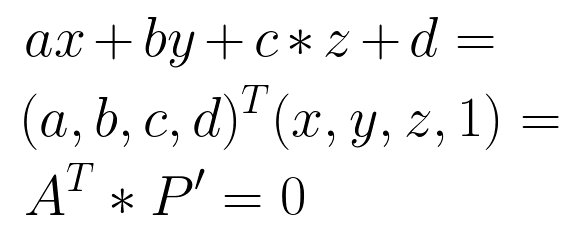
因此,点P在平面A上的充分必要条件就是平面A 向量与P的齐次坐标P'的内积(点乘):
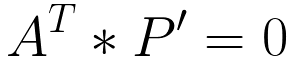
2、方便表达直线与直线,平面与平面的交点
先给出结论,后面再具体解释:
结论:在齐次坐标下,可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l,也就是
l = p x q
也可以使用两条直线 l, m 的叉乘表示他们的交点 x
x = l x m
见下面示例图。
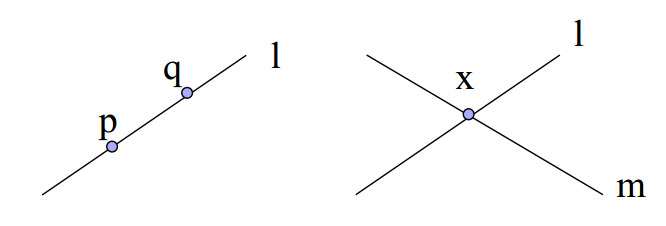
之所以可以这么简洁的表示交点是因为采用了齐次坐标的表示方式。
那么这是为什么呢?
先介绍一下叉乘(也称叉积、外积)的概念:
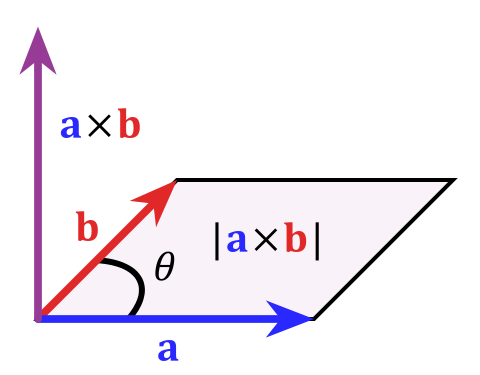
两个向量 a和b 的叉乘仅在三维空间中有定义,写作 a x b
a x b 是与向量 a, b都垂直的向量,其方向通过右手定则(见下图)决定。
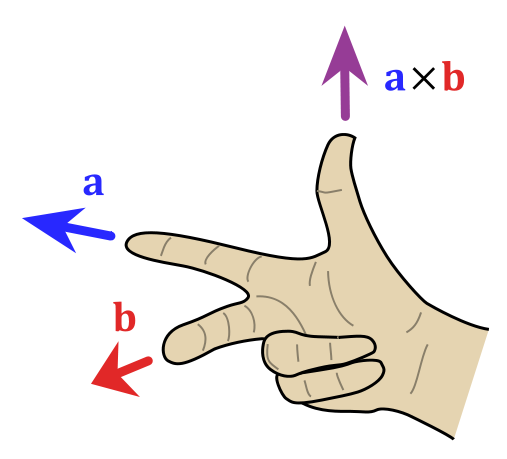
其模长等于以两个向量为边的平行四边形的面积(见下图)。
叉乘可以定义为:

其中 θ表示a, b的夹角(0°到180°之间),||a||, ||b||是向量a, b的模长
n则是一个与向量a, b所构成的平面垂直的单位向量
根据叉乘定义:
向量自身叉乘结果为0,因为夹角为0。也就是说三维向量 a x a =0, b x b = 0而点乘(也称点积,内积)的定义是
a * b = ||a||* ||b|| *cos(θ)
根据定义:如果两个向量垂直,cos(θ) = 0,点积也为0。
好了,经过上面点乘和叉乘定义的铺垫。下面来推导一下上面的结论:
为什么两条直线 l, m 的叉乘 l x m 等于它们的交点 p,也就是 p = l x m?
原因如下:首先,根据前面叉乘的定义,l x m 的结果向量(记为 p = l x m) 与 l 和 m都垂直,根据点乘的定义,垂直的向量之间的点积为0,因此可以得到:
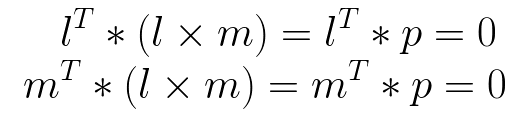
因此,根据前面点在直线上的结论,可以看到p既在直线l 上又在直线m上,所以 p = l x m 是两条直线的交点。此处 p 是齐次坐标。
同样的,可以证明,两点p, q 的叉乘 可以表示 过两点的直线l,即 l = p x q。(留做作业)
3、如何区分一个向量和一个点
先给出结论:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
具体解释见:
http://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
4、能够表达无穷远
比如 两条平行的直线 ax+by+c=0, ax+by+d=0,
可以分别用向量 l = (a, b, c), m = (a, b,d)表示
根据前面直线交点的计算方法,其交点为 l x m
根据叉乘计算法则
向量

的叉乘结果可以用如下方法计算得到

最终:l x m = (d-c)(b,-a,0),忽略标量(d-c),我们得到交点为(b,-a,0),并且是齐次坐标,如果要转化为非齐次坐标,那么会得到 (b/0, a/0),坐标是无穷大,可以认为该点为无穷远点,这与我们通常理解的:平行线相交于无穷远的概念相吻合。
因此,如果一个点的齐次坐标中,最后一个元素为0,则表示为无穷远点。
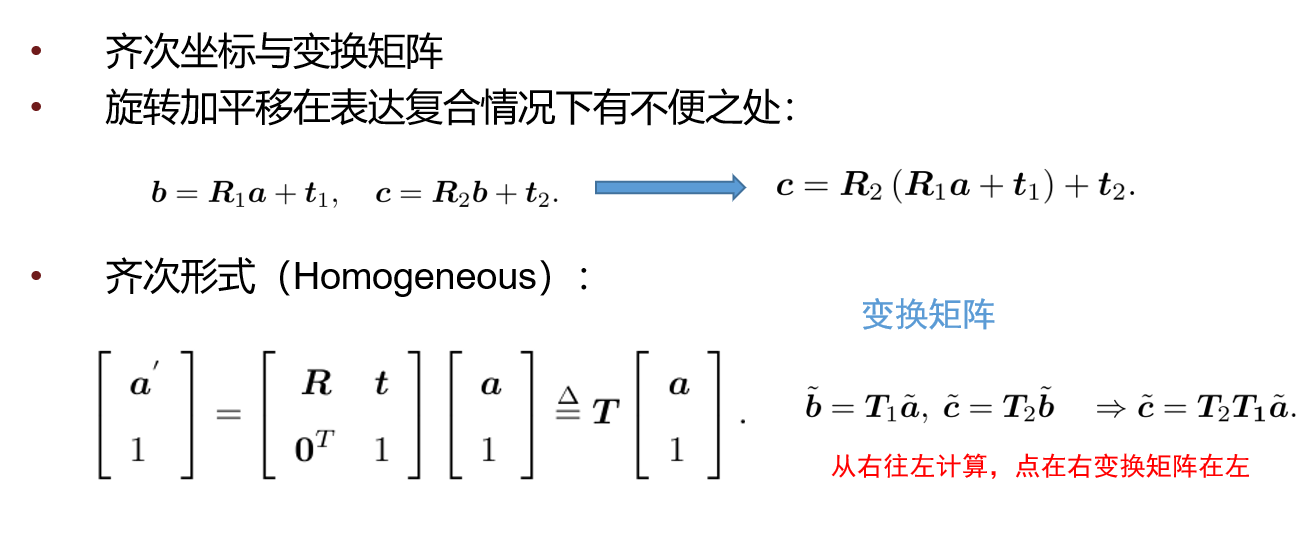
5、更简洁的表达欧氏空间变换
这是齐次坐标最重要的一个优势之一。在以后的学习中你会更加深刻的理解。
使用齐次坐标,可以方便的将加法转化为乘法,方便的表达平移。
比如我们要完成将2D坐标点x=[u,v]' 平移t=[tu, tv],如果用非齐次方法的话,是用如下的加法
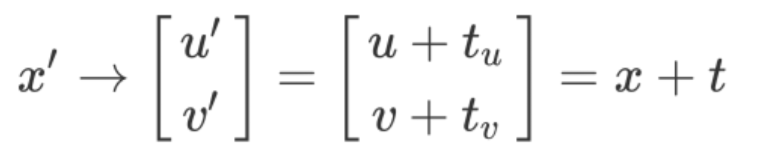
如果用齐次坐标表示时可以将加法转换为乘法

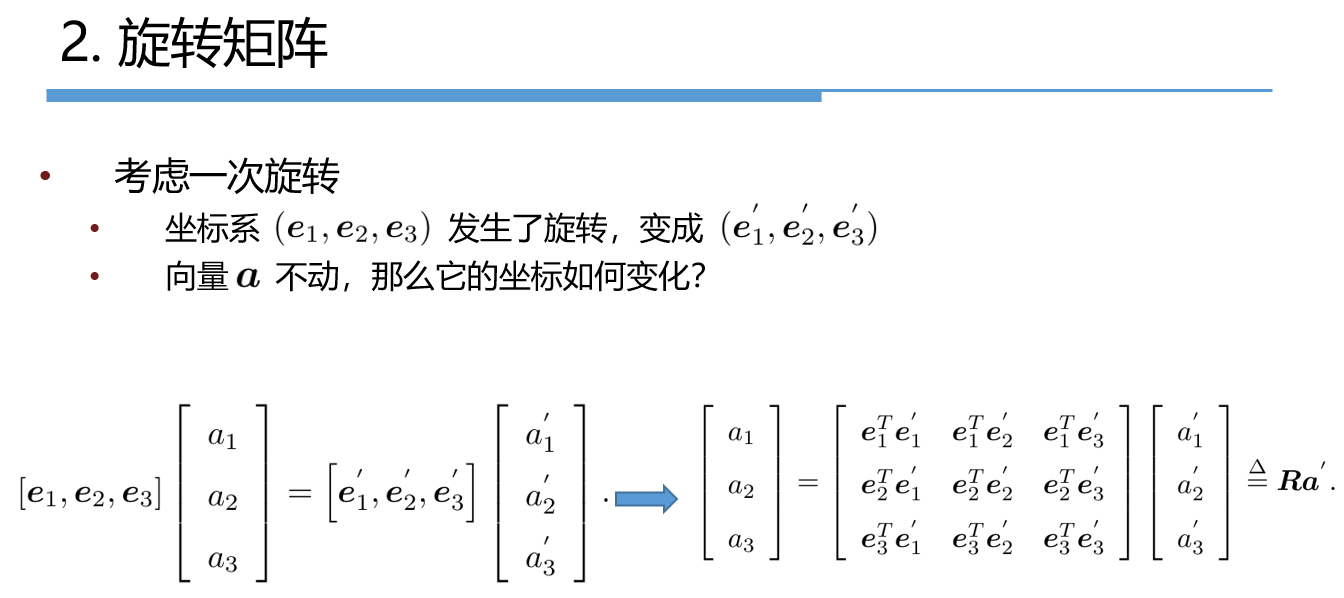
在欧氏变换中一般有两种操作:旋转和平移。
如果我们想要将向量a进行一个标准的欧氏变换,一般是先用旋转矩阵R进行旋转,然后再用向量t进行平移,其结果a' = R*a + t,这样看起来没什么问题。
但是,我们知道SLAM中一般都是连续的欧氏变换,所以会有多次连续的旋转和平移,假设我们将向量a进行了两次欧氏变换,分别为R1, t1 和 R2,t2,分别得到:
b = R1*a + t1, c = R2*b + t2
最终的结果 c = R2*(R1*a + t1) + t2
显然,这样的变换在经过多次后会变的越来越复杂。其根本原因是上述表达方式并不是一个线性的变换关系。
此时,齐次坐标就显示出它的魅力了,如果使用齐次坐标来表达 a' = R*a + t 的话可以写为:
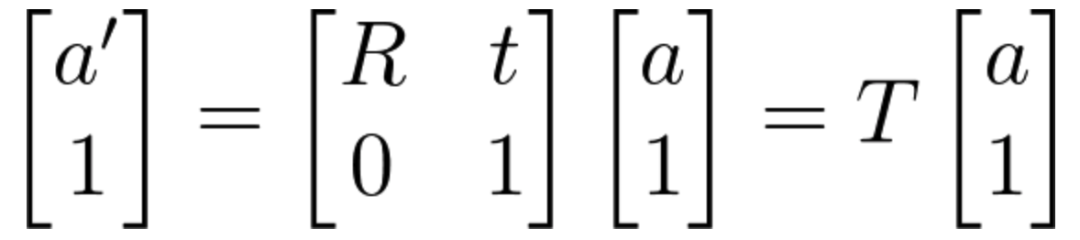
旋转和平移可以用一个矩阵T来表示,该矩阵T称为变换矩阵(transform matrix),这样欧氏变换就变成了线性关系,进行多次欧氏变换只需要连乘变换矩阵就行了,比如前面的两次欧氏变换使用齐次坐标就可以表示为:
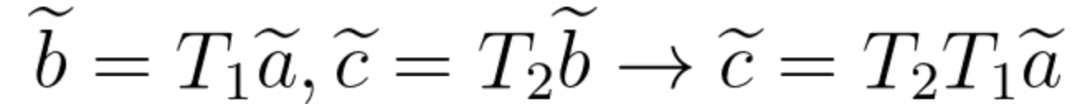
其中,波浪号代表齐次坐标。一般的,在SLAM中,b = Ta 的形式默认都是齐次坐标。
