使用单高斯模型来建模有一些限制,例如,它一定只有一个众数,它一定对称的。举个例子,如果我们对下面的分布建立单高斯模型,会得到显然相差很多的模型:

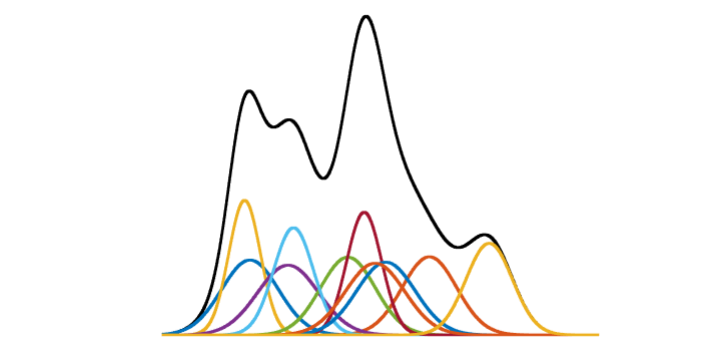
于是,我们引入混合高斯模型(Gaussian Mixture Model,GMM)。高斯混合模型就是多个单高斯模型的和。它的表达能力十分强,任何分布都可以用GMM来表示。例如,在下面这个图中,彩色的线表示一个一个的单高斯模型,黑色的线是它们的和,一个高斯混合模型:
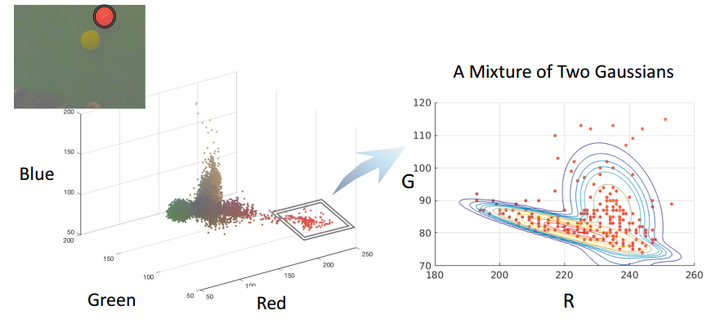
在小球检测的栗子中,我们试图对红色小球建立单高斯模型(红和绿这二元),会发现红色小球的观测值不是很符合所建立的模型,如下图:

此时,如果我们采取高斯混合模型(两个二元高斯分布),会发现效果好了很多,如下图:
下面,我们来详细地介绍一下高斯混合模型,高斯混合模型的数学形式如下:
其中,是均值为
,协方差矩阵为
的单高斯模型,
是
的权重系数(
),
是单高斯模型的个数。
前面我们提到了GMM的优点(能够表示任何分布),当然GMM也有缺点。其一,参数太多了,每一个单高斯模型都有均值、协方差矩阵和权重系数,另外还有单高斯模型的个数也是其中一个参数,这使得求解GMM十分复杂。其二,有时候所建立的高斯混合模型对观测值的建模效果很好,但是其他值可能效果不好,我们称这个缺点为过度拟合(Overfitting)。
2、求解高斯混合模型:EM算法
在求解单高斯分布的时候,我们用最大似然估计(MLE)的方法得到了理论上的最优解。当我们使用相同的方法试图求解高斯混合模型的时候,会卡在中间步骤上(具体来说,是单高斯分布求和出现在了对数函数里面)。索性我们可以用迭代的方法来求解GMM,具体来说,最大期望算法(Expectation Maximization algorith,EM)。
上一节提到,我们想要求解GMM如下:
这其中需要求解的变量很多:、
、
、
。为了简化问题,我们假定
是预先设定好的,并且每个单高斯分布的权重相等,即假定:
这样,我们需要确定的就只剩下每个单高斯分布的参数(、
)了。
前面提到,这个模型是没有解析解(理论最优)的。取而代之,我们采取迭代的方法逼近最优解(大家可以回想一下牛顿法求近似求解方程,或者遗传算法)。
在牛顿法中,我们需要预先猜测一个初始解,同样在EM算法中,我们也需要预先猜测一个初始解()。
在EM算法中,我们引入一个中间变量,其中
是单高斯分布的个数,
是观测值的数目。
直观地可以这样理解:在确定了所有单高斯分布之后,可以计算观测值发生的概率(分母部分)和第
个单高斯分布
下观测值
发生的概率(分子部分),这样
就可以理解为第
个高斯分布对观测值
发生的概率的贡献了。如下表所示:
表中最后一行可以理解为第
个单高斯分布对整个GMM的贡献。
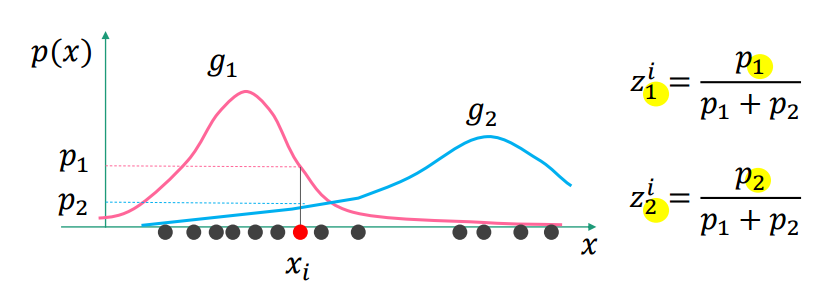
例如,当GMM中时(即由两个单高斯分布组成):
在这个图中,对于观测值![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) ,
,![[公式]](https://www.zhihu.com/equation?tex=p_1%2F2) 是第一个单高斯分布
是第一个单高斯分布![[公式]](https://www.zhihu.com/equation?tex=g_1%0A) 下
下![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) 发生的概率,
发生的概率,![[公式]](https://www.zhihu.com/equation?tex=p_2%2F2) 是第二个单高斯分布
是第二个单高斯分布![[公式]](https://www.zhihu.com/equation?tex=g_2%0A) 下
下![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) 发生的概率,
发生的概率,![[公式]](https://www.zhihu.com/equation?tex=%28p_1%2Bp_2%29%2F2) 是在整个GMM下
是在整个GMM下![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) 发生的概率;
发生的概率;![[公式]](https://www.zhihu.com/equation?tex=z_1%5Ei%3D%5Cfrac%7Bp_1%7D%7Bp_1%2Bp_2%7D) 表示
表示![[公式]](https://www.zhihu.com/equation?tex=g_1) 对
对![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) 发生概率的贡献,
发生概率的贡献,![[公式]](https://www.zhihu.com/equation?tex=z_2%5Ei%3D%5Cfrac%7Bp_2%7D%7Bp_1%2Bp_2%7D) 表示
表示![[公式]](https://www.zhihu.com/equation?tex=g_2) 对
对![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%7Bx_i%7D) 发生概率的贡献。
发生概率的贡献。
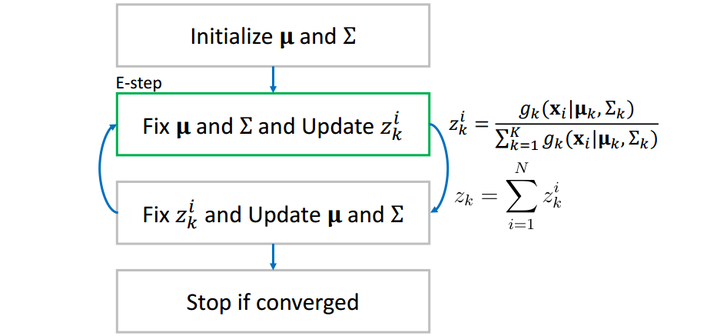
当我们算出了所有的![[公式]](https://www.zhihu.com/equation?tex=z_k%5Ei) 之后,我们再反过来用它更新每一个单高斯分布。更新的公式为:
之后,我们再反过来用它更新每一个单高斯分布。更新的公式为:![[公式]](https://www.zhihu.com/equation?tex=%0A%5Cboldsymbol%5Cmu_k+%3D+%5Cfrac%7B1%7D%7Bz_k%7D%5Csum_%7Bi%3D1%7D%5ENz_k%5Ei%5Cboldsymbol%7Bx_i%7D%0A%0A)
![[公式]](https://www.zhihu.com/equation?tex=%5CSigma_k+%3D+%5Cfrac%7B1%7D%7Bz_k%7D%5Csum_%7Bi%3D1%7D%5ENz_k%5Ei%28%5Cboldsymbol%7Bx_i%7D-%5Cboldsymbol%5Cmu_k%29%28%5Cboldsymbol%7Bx_i%7D-%5Cboldsymbol%5Cmu_k%29%5ET%0A)
大家可以想一想,对于第个高斯分布
,
可以理解为第
个观测值
的贡献,而
表示
的平均值,用
来更新
就很好理解了,进而再更新协方差矩阵
。
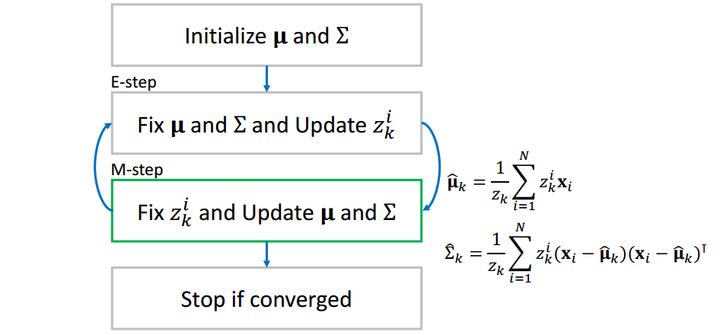 这样,两组值互相更新,当相邻两个步骤值的差小于事先设定一个阈值(threshold)时(收敛),我们停止循环,输出
这样,两组值互相更新,当相邻两个步骤值的差小于事先设定一个阈值(threshold)时(收敛),我们停止循环,输出![[公式]](https://www.zhihu.com/equation?tex=%5Cboldsymbol%5Cmu_k) 和
和![[公式]](https://www.zhihu.com/equation?tex=%5CSigma_k) 为所求。
为所求。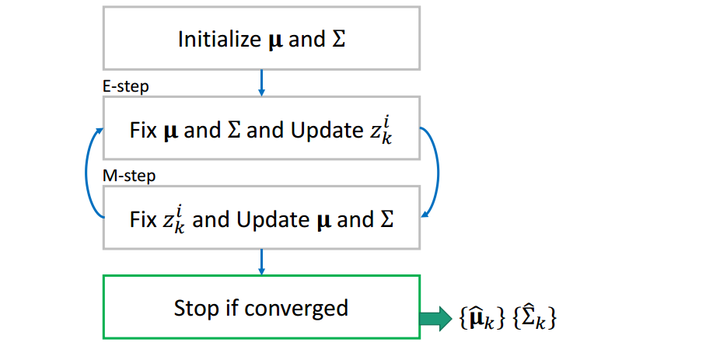
值得一提的是,EM算法的结果和初值有很大关系,不同初值会得到不同的解。(想象一下GMM模型其实是多峰的,不同的初值可能最终收敛到不同的峰值,有的初值会收敛到全局最优,有的初值会收敛到局部最优)
实战:小球检测
具体任务在这个网址:小球检测
简单来说,给你一些图片作为训练集,让你对黄色小球进行建模,建模完成后,读入最左边的原始图片,要求能像最右边的图片一样标识出小球的位置:

(注:我们使用matlab完成所有代码)
第一步:建立颜色模型
前面几节我们提到,要建立高斯分布模型,首先要有很多观测值,所以,我们将在这一步里面采集很多观测值,再建立高斯模型。课程里面提供了19张图片作为训练集供采样:
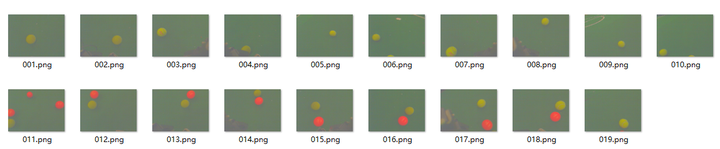 我们编写代码mark.m,作用为读入一张一张图片,然后手动圈出图片中的黄色小球,将圈中部分的像素RGB值存入观测值。
我们编写代码mark.m,作用为读入一张一张图片,然后手动圈出图片中的黄色小球,将圈中部分的像素RGB值存入观测值。
imagepath = './train'; Samples = []; for k=1:19 I = imread(sprintf('%s/%03d.png',imagepath,k)); % read files into RGB R = I(:,:,1); G = I(:,:,2); B = I(:,:,3); % Collect samples disp(''); disp('INTRUCTION: Click along the boundary of the ball. Double-click when you get back to the initial point.') disp('INTRUCTION: You can maximize the window size of the figure for precise clicks.') figure(1), mask = roipoly(I); figure(2), imshow(mask); title('Mask'); sample_ind = find(mask > 0); % select marked pixels R = R(sample_ind); G = G(sample_ind); B = B(sample_ind); Samples = [Samples; [R G B]]; % insert selected pixels into samples disp('INTRUCTION: Press any key to continue. (Ctrl+c to exit)') pause end save('Samples.mat', 'Samples'); % save the samples to file figure, scatter3(Samples(:,1),Samples(:,2),Samples(:,3),'.'); title('Pixel Color Distribubtion'); xlabel('Red'); ylabel('Green'); zlabel('Blue');
 结果我们采集了6699个观测值,散点图如下:
结果我们采集了6699个观测值,散点图如下: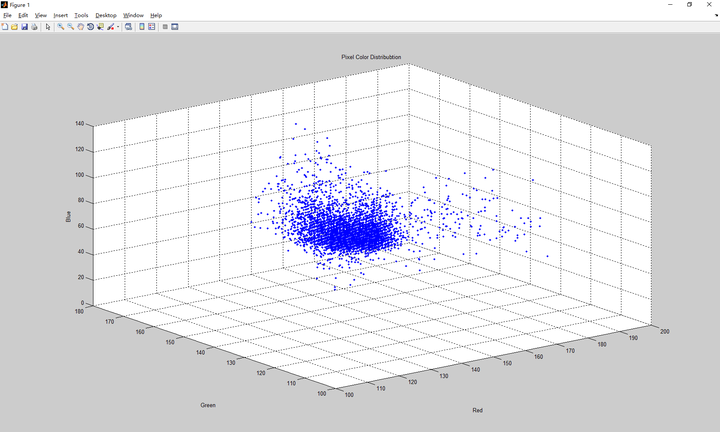 我们选用多元高斯分布作为我们的模型,应用第四节中的结论,编写代码coefficient.m求出平均值
我们选用多元高斯分布作为我们的模型,应用第四节中的结论,编写代码coefficient.m求出平均值和协方差矩阵
并存储到本地以供后续使用。
mu = mean(Samples); % mu sig=zeros(3,3); % sigma for i=1:N data=double(Samples(i,:)); sig=sig+(data-mu)'*(data-mu)/N; end % save the coefficients to files save('mu.mat', 'mu'); save('sig.mat', 'sig');
接下来,我们需要编写函数detecBall,以图像为参数,以划分好的黑白图像和小球中心为输出,如下,I是输入的图像,segI是划分好的黑白图像,loc是球的中心点。detecBall.m的具体代码如下:
function [segI, loc] = detectBall(I) load('mu.mat'); load('sig.mat'); Id=double(I); % array in size of (row, col, 3) row=size(Id,1); col=size(Id,2); % x_i - mu for i=1:3 Id(:,:,i) = Id(:,:,i) - mu(i); end % reshape the image to a matrix in size of (row*col, 3) Id=reshape(Id,row*col,3); % calc possibility using gaussian distribution % be careful of using * and .* in matrix multiply Id = exp(-0.5* sum(Id*inv(sig).*Id, 2)) ./ (2*pi)^1.5 ./ det(sig)^0.5; % reshape back, now each pixels is with the value of the possibility Id=reshape(Id,row,col); % set threshold thr=8e-06; % binary image about if each pixel 'is ball' Id=Id>thr; % find the biggest ball area segI = false(size(Id)); CC = bwconncomp(Id); numPixels = cellfun(@numel,CC.PixelIdxList); [biggest,idx] = max(numPixels); segI(CC.PixelIdxList{idx}) = true; %figure, imshow(segI); hold on; S = regionprops(CC,'Centroid'); loc = S(idx).Centroid; %plot(loc(1), loc(2),'r+');
需要注意的一点是,求像素属于小球的概率的时候,尽量用矩阵运算,而不要用循环,否则会效率低下,请读者仔细揣摩计算技巧,灵活运用矩阵的运算。
接下来,我们就可以测试小球检测的效果啦!
我们编写test.m测试训练集的19张图片:
imagepath = './train'; for k=1:19 I = imread(sprintf('%s/%03d.png',imagepath,k)); [segI, loc] = detectBall(I); figure, imshow(segI); hold on; plot(loc(1), loc(2), '+b','MarkerSize',7); disp('Press any key to continue. (Ctrl+c to exit)') pause end
效果如下: